16 Instrumental Variable Estimation
도구변수는 교란과 선택 편향 조정에 필요한 모든 변수들이 식별되고 정확하게 측정되어야 한다는 기존의 가정에서 벗어나 대안적 가정을 통해서도 타당하게 인과 효과를 추정할 수 있도록 하는 방법이다.
16.1 The three instrumental conditions
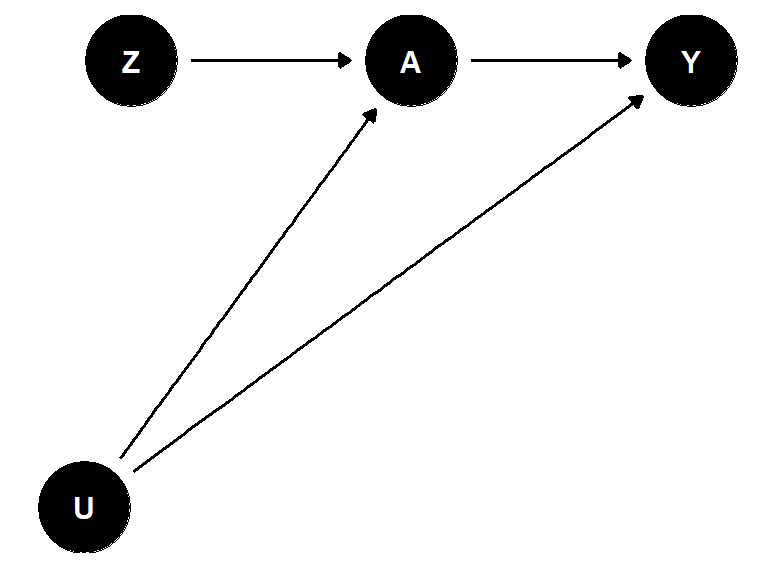
아래의 그림은 무작위 시행을 보여준다: \(Z\)는 무작위로 배정된 처치와 플라시보에 대한 식별 변수(1: 처치, 0: 플라시보)이고 \(A\)는 처치를 받았는지 여부(1: 처치 받음, 0: 처치 안받음)를 나타낸다. \(Y\)는 결과변수를, \(U\)는 결과와 처치에 영향을 미치는 모든 요인들을 의미한다.
여기에서 참여자들은 (1) 처치군에 해당할지 혹은 플라시보 군에 해당할지 알 수 없고, (2) 처치를 받을지 혹은 받지 않을지(플라시보에도 마찬가지로) 알 수 없기 때문에 이러한 연구를 이중 블라인드 플라시보 통제 무작위 시행(double-blind-placebo-controlled randomized trial)이라고 한다.
여기서 \(A \rightarrow Y\)에 대해 알고 싶다고 할 때, 우리는 \(A \leftarrow U \rightarrow Y\)의 뒷문 경로를 차단하기 위해 변수들을 정확하게 측정하고 조정할 필요가 있다. 하지만 실제로 우리는 모든 변수들을 식별하지도, 완벽하게 측정하지도, 그리고 모두 모델에 포함하지도 못하기 때문에 필연적인 효과 추정량의 편향을 경험하게 된다.
도구변수(IV)는 이와 같은 정확한 측정과 관련된 가정을 취하지 않는다. 도구변수 방법은 \(U\)에 의해 야기되는 교란을 조정하기 위해 일반적으로 요구되는 변수들을 측정하지 않을 경우에도 무작위 시행에서 \(A\)의 \(Y\)에 대한 평균 인과효과를 식별하고자 하는 노력이다. 이를 위해서 도구변수 \(Z\)는 다음과 같은 조건을 요구한다:
\(Z\)는 처치 \(A\)와 관계가 있다.
\(Z\)는 \(A\)에 대한 잠재적 효과를 통해서만 \(Y\)에 영향을 미친다.
\(Z\)와 \(Y\)는 공통 원인을 갖지 않는다(즉, \(X\rightarrow Z, X\rightarrow Y\)인 \(X\)는 존재하지 않는다는 것이다.)
위의 그림은 처치 \(A\)에 대한 도구변수 \(Z\)가 인과 효과를 가지는 특별한 사례이다. 이 때의 \(Z\)는 인과적 도구(causal instrument)라고 불린다. 때로는 이러한 인과적 도구가 측정되지 않아서 측정되지 않은 인과적 도구인 \(U_Z\)와 관계가 있는 일종의 대리변수나 대리도구(surrogate instrument)를 사용하기도 한다. 아래의 그림이 대리도구의 사례를 나타낸다.
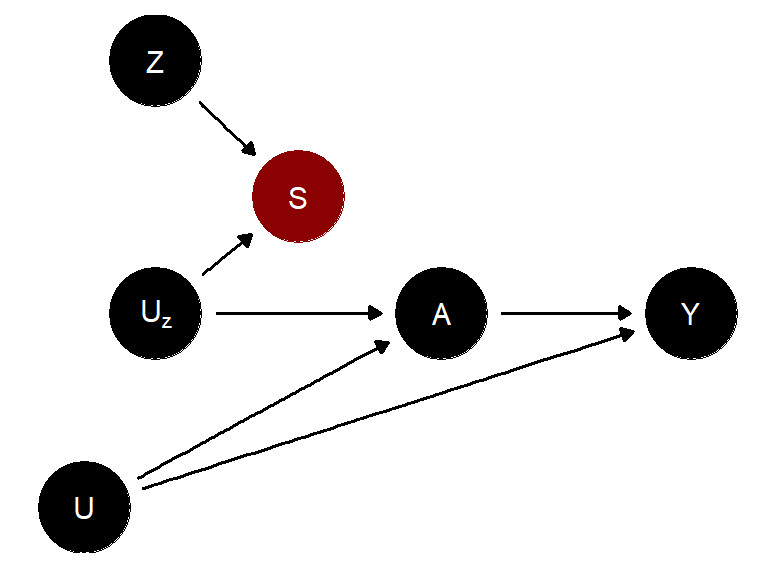
관측연구에서는 무작위로 배정된 지시변수가 없기 때문에, 위에 언급한 도구적 조건들을 가급적 충족시키는 변수를 통해 이를 도구변수라고 주장할 수 있다.
그런데 두 번째 조건과 세 번째 조건, 즉 \(Z\)는 \(A\)에 대한 잠재적 효과를 통해서만 \(Y\)에 영향을 미친다는 가정과 \(Z\)와 \(Y\)는 공통 원인을 갖지 않는다는 가정은 경험적으로는 입증될 수 없다. 우리가 식별가능한 모든 요인들의 인과관계 혹은 상관관계를 파악할 수 있는 것은 아니기 때문이다. 따라서 이 두 조건에 대해서는 단지 충족될 수 있을 것이라고 가정만 할 수 있을 따름이다.
관측연구에서는 제안된 도구 \(Z\)가 진정한 도구라는 것을 증명할 수 없기 때문에, \(Z\)를 제안된 또는 후보 도구(proposed or candidate instrument)라고 부른다. 우리가 할 수 있는 최선은 분야별 지식을 사용해 제안된 도구 \(Z\)가 두 번째 조건과 세 번째 조건을 충족한다고 합리적으로 가정할 수 있는 이유를 설명하는 것이다.
16.2 The usual IV estimand
\[ \frac{E[Y|Z = 1]-E[Y|Z = 0]}{E[A|Z = 1]-E[A|Z = 0]} = \mathrm{Usual\: IV\: estimand\: for\: a \: dichotomous instrument} \]
\[ \frac{\mathrm{Cov}(Y, Z)}{\mathrm{Cov}(A, Z)} = \mathrm{Usual\: IV\: estimand\: for\: a \: continuous instrument} \]
표준적인 IV 추정량을 계산하는 방법은 2SLS(two-stage-least-squares estimator) 추정량을 사용하는 것이다.
1단계에서 도구변수와 처치 간의 회귀식을 적합하고(\(E[A|Z] = \alpha_0 + \alpha_1Z\)), \(\hat{E[}[A|Z]\)을 구한다.
2단계에서는 결과변수에 대해 \(E[Y|Z] = \beta_0 + \beta_1\hat{E}[A|Z]\)를 적합한다.
이렇게 되면, 모수 추정치 \(\hat{\beta_1}\)은 \(Z \rightarrow A \rightarrow Y\)의 경로를 추정하는 것으로 다른 교란변수의 영향력을 배제하고 순수하게 \(Y\)로 가는 \(A\)의 효과를 포착할 수 있게 된다.
16.3 A fourth identifying condition: homogeneity
앞서 도구변수에 필요한 가정들은 경험적으로 검증될 수 없는 가정이라고 할 때, 추가적으로 네 번째 가정인 효과의 동질성(effect homogeneity)가 필요하다. 모든 개인에 걸쳐서 \(Y\)에 대한 처치 \(A\)의 효과가 일관되다는 가정이다. 하지만 이 네 번째 가정도 사실 받아들이기는 어렵다. 이미 우리는 개별 인과효과의 이질성이 존재할 수 있음을 알고 평균 인과효과에 초점을 맞춰오고 있다. 보다 일반적으로 이 동질성 가정은 결국 교란변수 \(U\)에 의한 효과 수정의 맥락에서 \(U\)의 모든 수준에서 \(A\)의 \(Y\)에 대한 평균 인과효과가 동일하다는 가정인 것이다. 측정되지 않은 교란변수 \(U\)가 효과 수정자일 수 있다는 점에서 이 세번째 가정은 때로는 성립되지 않는다. 동질성 조건을 통과하기 위해서는 두 가지 방법을 택할 수 있다:
IV 추정을 위해 모델에 기준이 되는 공변량을 투입하는 것이다.
효과의 동질성을 요구하지 않는 대안적 가정을 사용하는 것이다.
16.4 An alternative fourth condition: monotonicity
모든 개인에 대해 두개의 반사실적 처치변수 \(A^{z=1}\), \(A^{z = 0}\)의 값을 알고 있다면, 연구의 대상이 되는 모집단의 모든 개인들을 다음과 같은 네 개의 하위 집단으로 분류할 수 있을 것이다.
Always-takers: 배정된 처치 그룹에 관계없이 항상 처치를 받는 개인. 즉, \(A^{z=1} = 1\)과 \(A^{z=0} = 1\)이 모두 해당되는 개인.
Never-takers: 배정된 처치 그룹에 관계없이 처치를 절대 받지 않을 개인.
Compliers 또는 cooperative: 처치 그룹에 배정되면 처치를 받고, 통제 그룹에 배정되면 처치를 받지 않는 개인. 즉, \(A^{z=1} = 1\) 및 \(A^{z=0} = 0\)인 개인.
Defiers or contrarians: 처치를 받도록 배정된 경우 처치를 받지 않고, 처치를 받지 않기로 배정된 경우 처치를 받는 개인. 즉, \(A^{z=1} = 0\)이고 \(A^{z=0} = 1\)인 개인.
이제 동질성 조건을 새로운 단조성(monotonicity) 조건으로 대체해보자. 단조성 조건은 다음과 같다:
Defiers가 없다.이 경우, 평균 인과효과는
Always takers+Compliers의 효과가 된다.
단조성 조건 하에서 IV 추정량은 compliers의 처치의 평균 인과효과와 같게 된다:
\[ E[Y^{a=1}-Y^{a=0}|A^{z=1}=1,A^{z=0}=0]. \]
Always-takers와 Never-takers의 경우 \(Z\)가 \(Y\)에 미치는 영향은 정확히 0이다. 왜냐하면 \(Z\)의 효과는 전적으로 \(A\)를 통해 매개되고 해당 하위집단에서 \(A\)의 값은 할당된 \(Z\)의 값과 상관없이 고정되어 있기 때문이다.
관측연구에서 IV 추정량은 defiers가 없을 때 compliers에서의 효과를 추정하는 데 사용될 수 있다. 사실 관측연구에서는 제안된 도구변수인 \(Z\)가 무작위로 배정된 것이 아니라는 점에서 compliers 또는 defiers가 존재하지 않지만 여기서의 각 용어는 \(A^{z=1}=1, A^{z=0}=0\)이거나 \(A^{z=1}=0, A^{z=0}=1\)인 개인을 지칭하는 데 사용된다.
효과의 동질성이 아니라 단조성을 가정하면 여러 모로 편하지만 비판점도 분명히 존재한다:
compliers에서의 효과의 적실성에 대한 의문관측연구에서 단조성이 항상 합당한 가정은 아니라는 것: 실험 연구에서야 처치 받는 애들은 다 처치 받고 아닌 애들은 아니었지만 관측 연구에서는 처치 변수가 무작위로 배정된 것이 아니니만큼
defiers가 없다고 가정하는 것에 대해서 제기될 수 있는 문제이다.많은 현실적인 환경에서
compliers의 하위 모집단은 잘 정의되지 않음. 실제로 이게 어떤 집단을 의미하는가?
16.5 The three instrumental conditions revisited
이 섹션에서 실제로 통계적 기준으로 어떠한 도구변수가 약한 도구변수인지 말하는 것은 크게 의미가 없는 것으로 보인다. 오히려 실질적인 의미, 과연 그 도구가 정말 도구변수로서의 가정을 충족하는 것이냐를 정당화하는 것이 핵심으로 보인다. 그리고 이러한 정당화는 어디까지나 도메인 지식에 크게 좌우된다고 할 수 있다.
16.6 Instrumental variable estimation versus other methods
도구변수 추정법은 조건부 교환가능성 가정을 다른 가정들로 대체한다는 점에서 차이가 있다.
상대적으로 도구변수 추정법의 조건 1-4의 사소한 위배가 큰 편향으로 이어질 수 있다: 도구변수 추정치의 민감성
표준적인 도구변수 추정법의 적용의 이상적인 조건은 다른 방법들에 비해 매우 제한적이다.
인과추론은 가정의 투명성과 서로 다른 가정들에 의존하는 방법들로부터의 결과들에 대한 교차검증에 의존한다. 이 점에서 IV 추정량을 사용할 때, 그 방법에 한계에 대해 명확하게 인지할 필요가 있다.