11 Why Model?

제1부는 대개 개념적인 내용들을 다루었다면, 제2부에서는 선형 모델이나 로지스틱 모델 등과 같은 회귀 모델을 적합하기 위한 컴퓨팅 작업 역시 요구한다. 이 챕터에서는 제1부에서 사용된 비모수 추정량(nonparametric estimators)과 제2부에서 사용되는 모수(모델 기반) 추정량(parametric estimators)의 차이에 대해 서술하고, 평활화(smoothing)와 모델링 결정과 관련된 편향-분산(bias-variance) 상반관계에 대해 검토한다.

11.1 Data cannot speak for themselves

우리가 원하는 것은 무작위로 표본추출된 개인들을 대상으로 그로부터 모집단에서 처치 수준이 \(A = a\)인 개개인들 간의 \(Y\)의 평균을 일관되게 추정하는 것이다. 즉, 모추정치(estimand)는 알려지지 않은 모집단의 모수 \(E[Y|A=a]\) 라고 할 수 있다.

\(E[Y|A=a]\) 에 대한 \(\hat{E}[Y|A=a]\) 이라는 추정량은 알수 없는 모집단의 모수를 추정하기 위해 사용되는 데이터에 대한 어떠한 함수이다.
우리는 모든 추정량이 일관되기를 원하며, 모집단의 평균을 추정하기 위해 표본의 평균을 사용하게 된다.

모집단에서의 \(A = a\) 의 처치를 받은 개개인들 간의 \(Y\) 의 평균에 대한 추정치(estimate)는 (알 수 없는 모집단 수준에서의) 추정량을 특정한 데이터셋에 적용한 결과로 나타난 숫자라고 할 수 있다.

이 챕터에서의 목적은 추정치에 인과적 해석이 있는지 여부와 관계없이 평균 \(E[Y|A = a]\) 와 같은 모집단의 수치를 추정할 때 모델이 필요하다는 것을 확인하는 것이다.

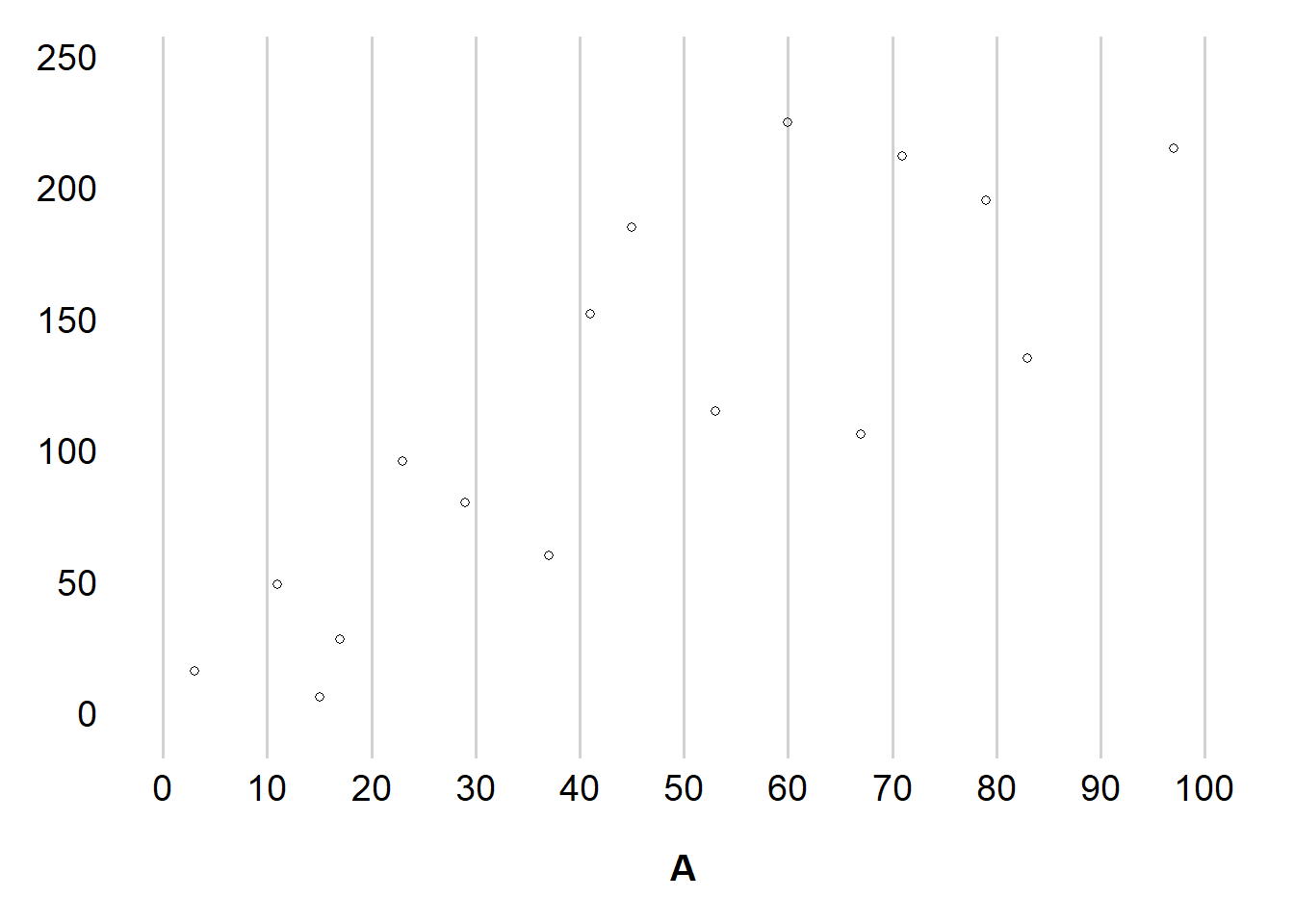
\(A\)가 치료 용량을 mg/일 별 0~100mg의 정수 값을 취한다고 해보자. Figure 11.1 은 16명의 각 개인에 대한 결과 값을 나타내는 데, 처치의 가능한 값의 수가 연구에 참여한 개인의 수보다 훨씬 많기 때문에 어떤 개인도 받지 못한 처치 \(A\)의 값이 많이 있다. 예를 들어, 이 예제에서 처치 \(A = 90\) 인 개인은 존재하지 않는다.

이 경우에 나타날 수 있는 문제가 바로 “어떻게 목적으로 하는 모집단에서 처치 수준 \(A = 90\) 인 개인들 간의 결과 \(Y\) 에 대한 평균을 추정할 수 있을 것인가 하는 것이다.
만약 처치 \(A\) 가 연속형 변수라면 표본 평균은 모든 처치 수준에서 거의 정의되지 못하게 될 것이다.
이 지점에서 우리는 모델을 통해서 데이터를 보조하는 것이 필요하다.

11.2 Parametric estimators of the conditional mean

앞에서와 마찬가지로 처치 수준 \(A = 90\) 인 개인들의 결과, \(Y\) 에 대한 평균을 추정하고자 한다고 할 때, 그 값은 처치 수준이 \(A = 80\) 인 경우와 \(A = 100\) 인 경우의 \(Y\)의 평균 값 사이에 놓여있을 것이라고 기대한다고 하자.

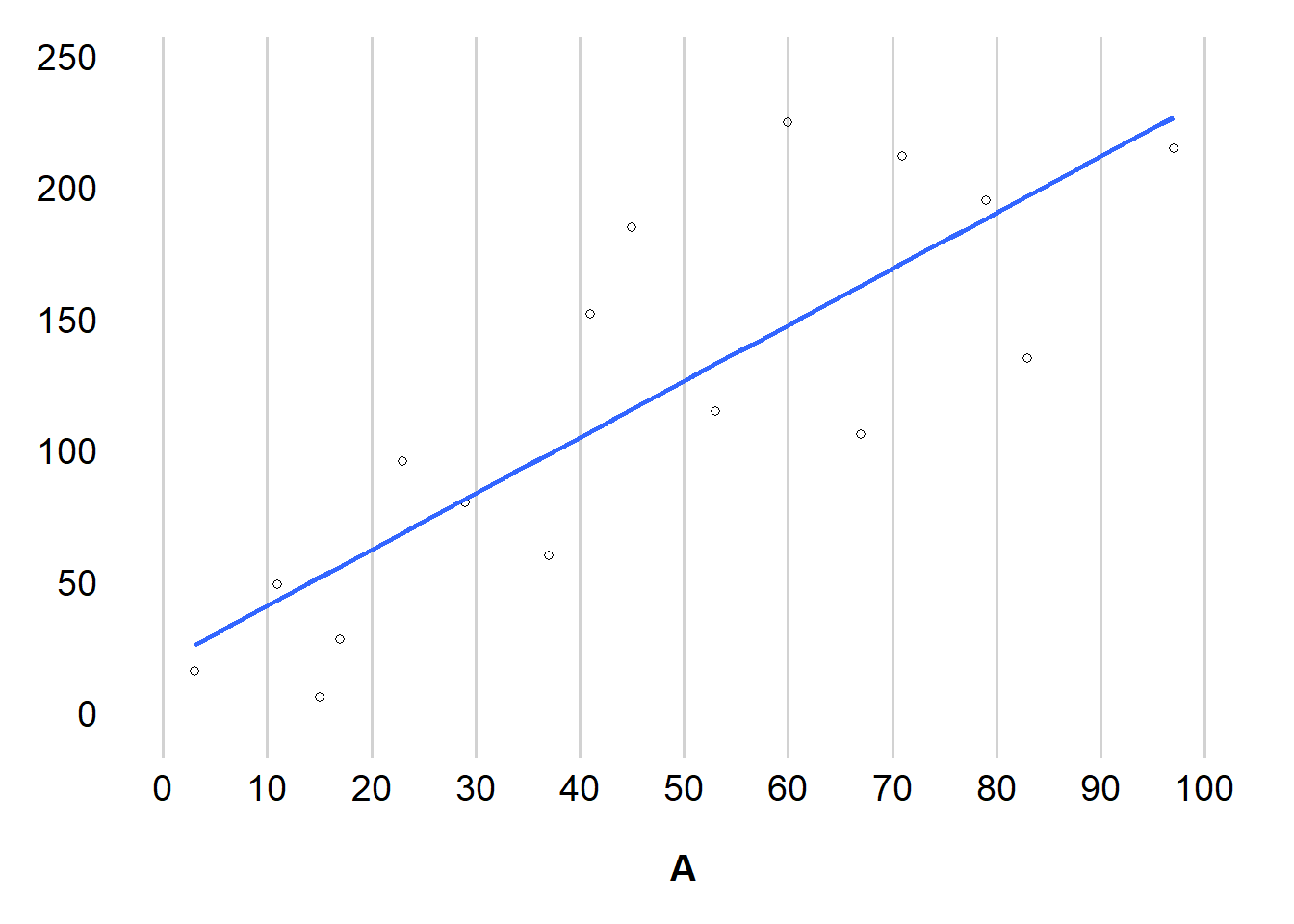
이때 우리는 \(Y\) 의 평균 값은 처치 \(A\) 값에 대한 선형 함수를 따른다는 것을 알고 있다 (Figure 11.1).
보다 정확하게는 \(A\)의 한 단위 별 증가량 \(\theta_1\)에 대해 \(Y\)에 대한 평균, \(E[Y|A]\)가 증가 또는 감소한다는 것을 알고 있다.

\[ E[Y|A] = \theta_0 + \theta_1 A \]

이러한 수식을 선형 평균 모델(linear mean model)이라고 한다.

\(\theta_0, \theta_1\): 모델의 모수(parameters)
이 모델에 Figure 11.1 의 데이터를 적용해 0부터 100 사이의 모든 값에 대한 \(E[Y|A = a]\) 를 추정해볼 수 있다.
이렇게 모델을 이용해서 각 개인에 대해 추정한 \(\hat{E}[Y|A]\)를 예측값(predicted value)이라고 한다.
최소제곱함(ordinary least squares) 방법을 통해서 모수 \(\theta_0, \theta_1\)에 대한 불편추정량을 얻을 수 있다.
각 관측치들과 모델로 추정한 예측값 사이의 차이를 표본 수준에서는 잔차(residuals)라고 한다.
잔차의 분산이 처치 \(A\)와 관계가 없을 때(동분산성; homoscedasticity), 우리가 얻은 추정량은 불편추정량(unbiased estimators)의 조건 중 하나를 갖추게 된다.

모델이란 데이터의 결합 분포에 대한 사전적 제약으로 정의될 수 있다.

예를 들어, 앞서의 선형모델은 조건부 평균 함수 \(E[Y|A]\)를 직선의 형태로 제약하고 있다.
모수적 모델을 사용할 때는 모델의 가정과 전제가 충족될 경우에만 그로 인해 도출된 추론이 옳다고 할 수 있다.

11.3 Nonparametric estimators of the conditional mean

\(A\)가 이산형 처치라고 하고, 처치군의 \(Y\)의 평균을 \(E[Y|A = 1]\), 통제군의 \(Y\)의 평균을 \(E[Y|A=0]\)으로 일관되게 추정하고자 한다고 하자. 이때, 사용하고자 선형 모델을 다음과 같다:

\[ E[Y|A] = \theta_0 + \theta_1 A \]

이 경우, 통제군은 \(E[Y|A=0] = \theta_0 + 0\times\theta_1 = \theta_0\), 처치군은 \(E[Y|A=1] = \theta_0 + 1\theta_1 = \theta_0 + \theta_1\)을 추정하게 된다. 즉, 처치의 효과는 \(\theta_1\)이라는 것을 확인할 수 있다.

이 모델은 \(E[Y |A = 1]\) 및 \(E[Y |A = 0]\)의 값에 어떠한 제한도 두지 않는다. 따라서 이산형 처치 \(A\)를 사용하는 \(E[Y |A = a] = \theta_0 + \theta_1 A\)는 표본 평균과 마찬가지로 데이터 그 자체로 얻을 수 잇는 결과를 보여주므로, 모델이라고 할 수 없다.
- “데이터 분포에 제한을 두지 않는 모델’은 포화 모델(saturated models)로, 모델에 대한 정의에 맞지 않더라도 형식적으로는 모델처럼 보이기 때문에 포화 모델도 일반적으로 모델이라고 부른다.
일반적으로 조건부 평균 모델에서의 모수의 수가 모집단 수준에서의 알려지지 않은 조건부 평균의 수와 동일할 때, 그 모델은 포화되었다고 한다.
반면에 소수의 모수들을 가지고 많은 모집단의 추정량을 추정하고자 할 때, 우리는 이 모델을 간명하다(parsimonious)라고 한다.
- 만약 한정된 데이터에 비해 너무 많은 모수를 가지고 추정하고자 한다면, 우리는 과소사례 과다변수의 문제에 직면하게 된다.

11.4 Smoothing

앞서 Figure 11.1 의 데이터와 선형 모델 \(E[Y|A] = \theta_0 + \theta_1 A\) 을 생각해보자.

\(\theta_1\): \(A\)의 한 단위 변화에 따른 결과의 평균 차이
Figure 11.2 는 가장 잘 들어맞는 직선으로 그 차이를 보여준다.

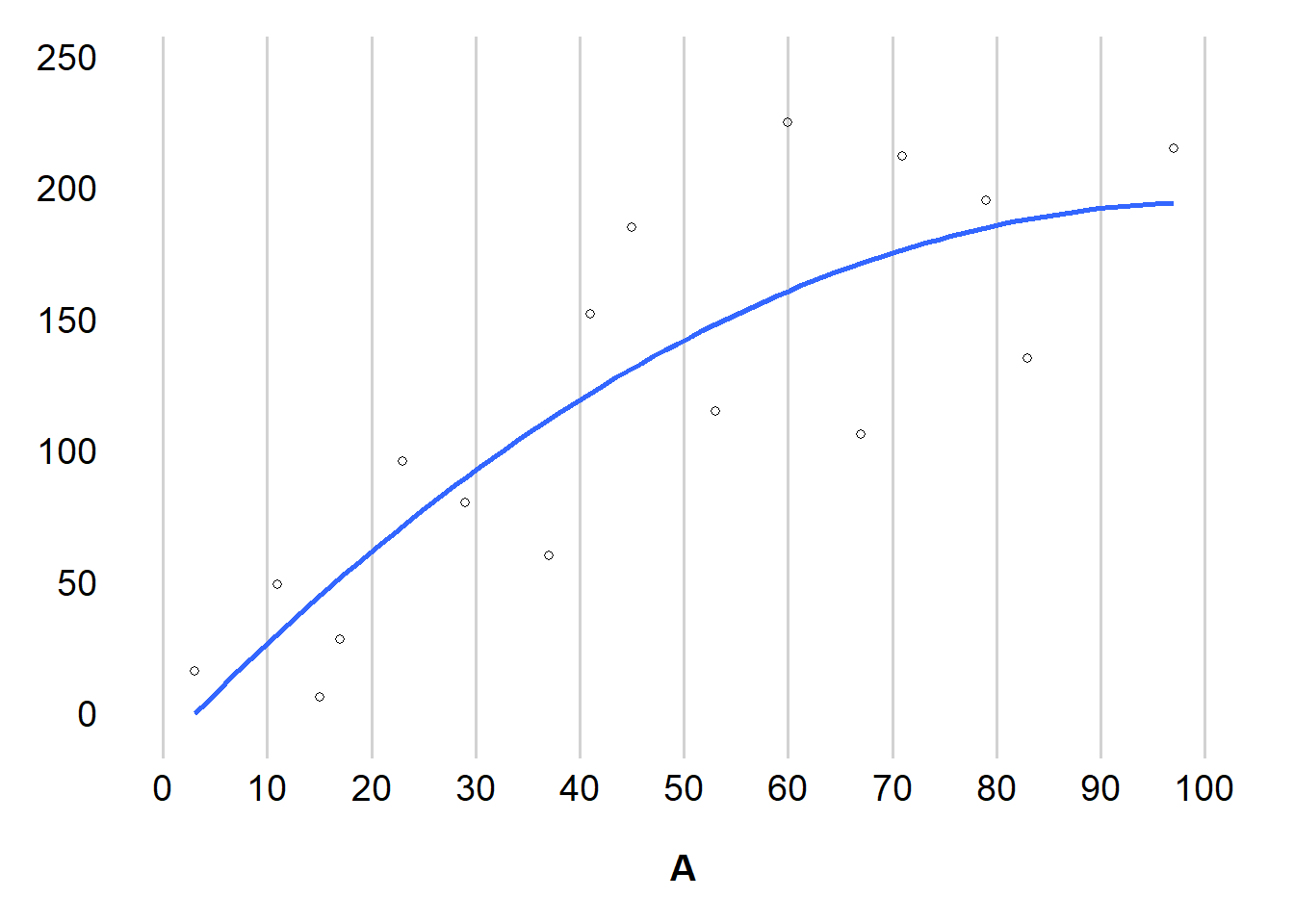
하지만 처치의 효과가 모든 개인에게 있어서 반드시 직선이 아닐 수도 있다. 이 경우에는 선형 모델에 약간의 변형을 주어 반영할 수 있다.

이차항(quadratic term), \(A^2\)를 선형 모델에 포함하여 비선형적 관계를 나타낼 수 있다.
이와 같이, 다차항을 얼만큼 포함할 것인가 하는 문제는 관측된 개개인들로부터 얼마나 정보를 얻느냐에 따라 좌우된다.

실제 적용에서 모델은 종종 다양한 공변량을 포함하므로 곡선은 초차원(hyperdimensional) 표면이 된다. 문제의 차원성과 관계없이 평활화의 개념은 변하지 않는다. 모델의 매개변수가 적을수록 예측하는 표면이 더 매끄러워진다.

11.5 The bias-variance trade-off

모수가 두 개인 모델, \(E[Y|A] = \theta_0 + \theta_1 A\)과 모수가 세 개인 모델 \(E[Y|A] = \theta_0 + \theta_1 A + \theta_2 A^2\)이 있다고 할 때, 서로 다른 두 모델로부터 얻은 추정치 중 어느 것이 더 우리가 알고자 하는 모집단의 평균에 근접한 것일까?

관계가 실제로 곡선인 경우 이 모델은 직선을 가정하기 때문에 2매개 변수 모델의 추정치가 편향될 것이다.
반면에 관계가 진정한 직선인 경우 두 모델의 추정치가 모두 유효하다.

일반적으로 모델의 매개변수 수가 많을수록 모델에 부과되는 제약이 적고, 모델이 덜 평활할수록 모델의 오특정(misspecification)으로 인한 편향으로부터 더 자유로울 수 있다. 덜 매끄러운 모델은 덜 편향된 추정치를 산출할 수 있지만, 더 큰 분산을 초래하기도 한다. 이것이 편향-분산 상반관계이다.