7 Confounding
“누군가가 하늘을 바라보면, 그것이 다른 보행자들로 하여금 하늘을 바라보게 할까?” 라는 인과적 질문에 답을 하고자 관측 연구를 수행하였다고 하자. 그런데 연구자는 보행자들이 위에서 큰 소음이 들릴 때 하늘을 올려다본다는 사실을 발견하였다. 따라서 두 번째 보행자가 하늘을 바라본 이유가 “첫 번째 보행자가 하늘을 바라보아서” 인지, 아니면 “큰 소음”이 들려서 인지는 불명확하다.
무작위 실험에서 처치는 말 그대로 무작위(randomly)로 이루어지지만 관찰 연구에서 처치는 여러 가지 요인에 의해 영향을 받을 수 있다. 만약 처치 이외의 요인들이 결과에 영향을 미친다면, 그러한 요인들의 효과는 처치의 효과와 중첩된다고 볼 수 있다. 이 경우 우리는 처치군과 통제군 간의 교환가능성이 결여된, “중첩”(confounding)이 존재한다고 한다.
7.1 The structure of confounding
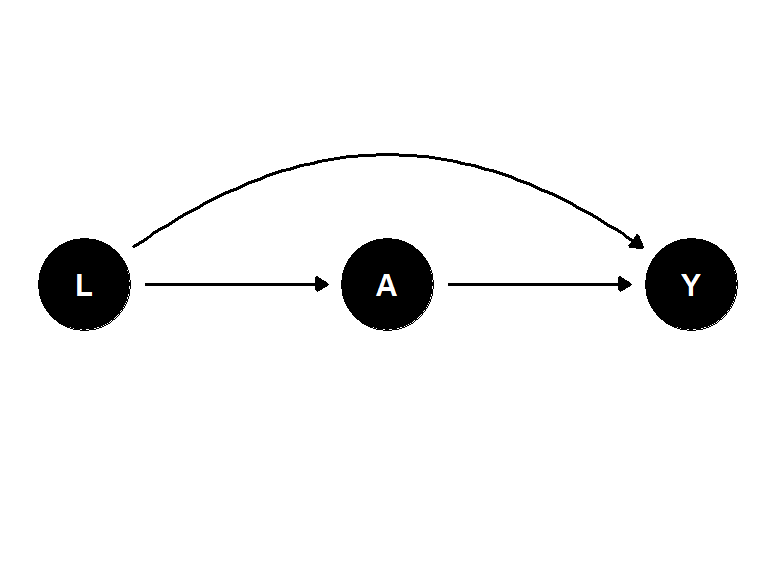
처치와 결과 모두에 영향을 미치는 공통 요인의 존재로 인해 나타나는 편향인 중첩의 구조는 인과 다이어그램으로 나타낼 수 있다. \(L\) 은 \(A\) 와 \(Y\) 모두에 영향을 미치는 공통 요인이다.
- \(A\rightarrow Y\) 는 \(A\) 의 \(Y\)에 대한 인과효과를 보여준다.
-
\(A \leftarrow L \rightarrow Y\) 는 공통요인 \(L\) 을 포함한 \(A\) 와 \(Y\) 간의 관계를 보여준다. 이때, 공통요인 \(L\) 은 뒷문경로(backdoor path)라고 할 수 있다.
- 즉, 직접적으로 영향을 미치는 것 외에 중간에 다른 공통요인을 경유하여 영향을 미치는 경로를 말한다.
공통 요인 \(L\) 의 존재는 처치 \(A\) 와 결과 \(Y\) 사이에 추가적인 관계성을 부여하며(직접적 영향이 아니라 \(L\) 을 경유하여), 이를 \(A\) 가 \(Y\) 에 미치는 영향에 대해 중첩이 존재한다고 한다.
7.2 Confounding and exchangeability
이제 중첩 개념을 교환가능성의 개념과 연관지어 이해해보자. 교환가능성 \(Y^a \perp\!\!\!\perp A\) 의 조건이 충족된다고 할 때, 평균 인과효과는 다른 변수들에 대한 조정 없이도 식별가능하다. 만약 교환가능성의 조건이 충족되지 않지만 조건적으로 충족되는 \(Y^a \perp\!\!\!\perp A|L\) 인 조건적 교환가능성-조건적 무작위 실험에서는 처치를 받을 확률이 \(L\) 의 값에 따라서 달라진다. 이 경우, \(L\) 의 값에 대해 알고 있다면, 평균 인과효과는 식별가능하다. 다만, \(L\)에 대해 표준화나 역확률 가중치 등을 이용한 조정의 노력이 필요하다. 조건부 교환가능성은 또한 계층화를 통해 \(l\) 의 값에 대해 \(E[Y^{a=1}|L=l] - E[Y^{a=0}|L=l]\) 조건적 인과효과를 식별할 수 있다.
인과 DAG로 어떻게 \(L\) 변수가 존재하는지, 조건부 교환가능성 조건이 충족되는지를 알 수 있을까? 두 가지 접근법이 있다:
- 인과 DAG에 뒷문 요건(backdoor criterion)을 적용
- 인과 DAG를 SWIG로 전환
\(L\)을 조건으로 하여 \(A\)와 \(Y\) 사이의 모든 뒷문 경로가 차단되고 \(L\)에 처치 \(A\) 의 영향을 받는 변수가 포함되어 있지 않은 경우, 공변량 \(L\) 은 뒷문 기준(backdoor criterion)을 충족한다. \(L\)이 뒷문 기준을 충족할 때에만 조건부 교환가능성의 조건이 충족된다. 뒷문 기준이 충족되는 조건은 다음과 같다:
- 처치와 결과 모두에 있어 공통의 원인이 존재하지 않는 경우: 중첩이 존재하지 않는다.
- 처치와 결과 간에 공통의 원인이 존재하지만 \(A\) 에 영향을 받지 않는 측정된 \(L\) 의 서브셋은 모든 뒷문 경로를 차단하기에 충분하다. 이 경우 “측정되지 않은 중첩”은 존재하지 않는다.
- 즉, 주어진 \(L\) 의 수준별로 처치와 통제 집단 간 교환가능성은 유지된다.
조건부 교환가능성이 뒷문 기준을 의미하는가? \(L\) 이 뒷문 기준을 충족한다고 하는 것은 항상 주어진 \(L\) 에서 조건부 교환가능성이 성립한다는 것을 의미한다. 마찬가지로 주어진 \(L\) 에서 조건부 교환가능성은 \(L\) 이 뒷문 기준을 충족한다는 것을 의미한다.
7.3 Confounding and the backdoor criterion
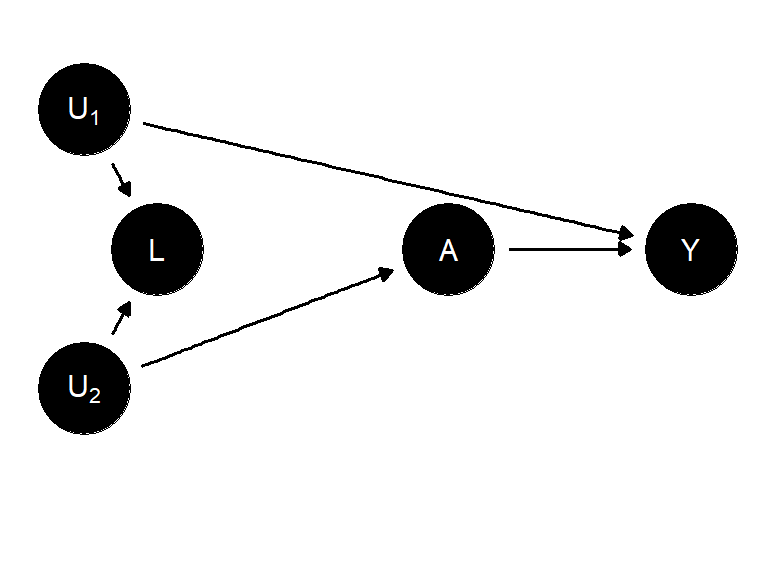
모든 인과 DAGs 의 노드들은 그 자체로 완벽하게 측정된 개념이라고 가정한다. 아래의 인과 다이어그램에서는 처치 \(A\) 와 결과 \(Y\) 간의 공통요인은 존재하지 않으므로 중첩은 존재하지 않는다고 할 수 있다.
\(L\) 을 통한 \(A\) 와 \(Y\) 간의 뒷문 경로 \((A \leftarrow U_2 \rightarrow L \leftarrow U_1 \rightarrow Y)\) 는 \(L\) 이 이 경로의 충돌인자이기 때문에 차단된다.
따라서 \(A\) 와 \(Y\) 간의 모든 관계는 \(Y\) 에 대한 \(A\) 의 효과로 인한 것이므로, 이때의 관계는 인과적 관계라고 할 수 있다.
만약 \(A\) 와 \(Y\) 의 데이터만으로 인과 효과를 식별할 수 있다면, \(L\) 은 교란인자(confounder, 혹은 중첩인자)가 아니라고 할 수 있다.
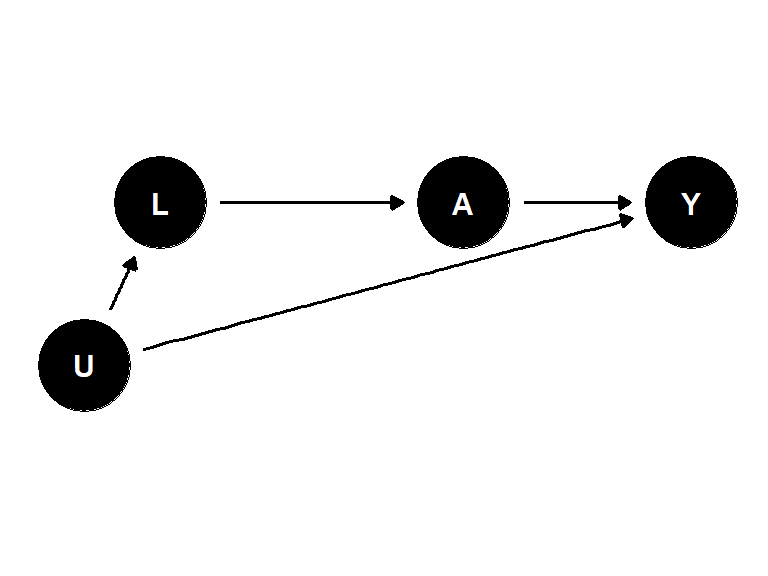
충돌인자 \(L\) 에 대해 조건적이라는 것은 \(A\) 와 \(Y\) 사이의 뒷문 경로를 열어놓게 되기 때문에\((A \leftarrow U_2 \rightarrow L \leftarrow U_1 \rightarrow Y)\), \(L\) 에 대한 조정은 편향을 야기하게 된다.
-
\(A\) 와 \(Y\) 간의 관계는 \(Y\) 에 대한 \(A\) 의 효과에서 온 관계에 더하여 이 개방된 뒷문 경로로 인한 관계도 포함한다.
\(A\) 가 \(Y\) 에 미치는 효과에는 순수한 \(A\) 만의 영향이 아니라 \(U_2\) 가 \(A\) 를 경유하여 미치는 영향도 포함되어 있기 때문이다.
이처럼 둘 중 하나가 \(A\) 와, 또 다른 하나가 \(Y\) 와 관계가 있는 한계 독립적인(marginally independent) 변수 \(U_1, U_2\) 의 공통 효과 \(L\) 에 조건적으로 인해 발생하는 편향성을 선택편향(selection bias)라고 한다.
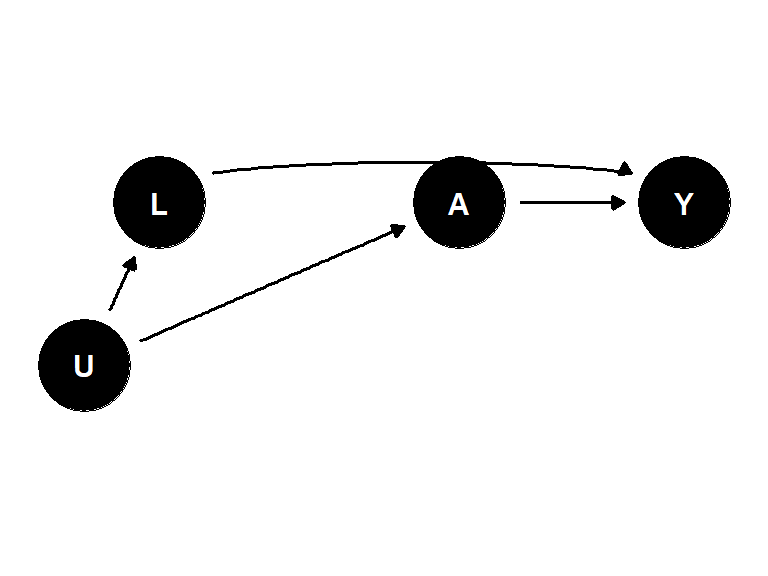
위의 인과 다이어그램에서 \(L\) 은 \(A\) 와 \(Y\) 의 공통 원인이 아니지만 여전히 \(A\) 와 \(Y\) 의 공통 원인인 관측되지 않은 \(U\) 에 대한 열린 뒷문 경로를 차단할 필요가 있기 때문에 \(L\) 은 교란요인이라고 할 수 있다.
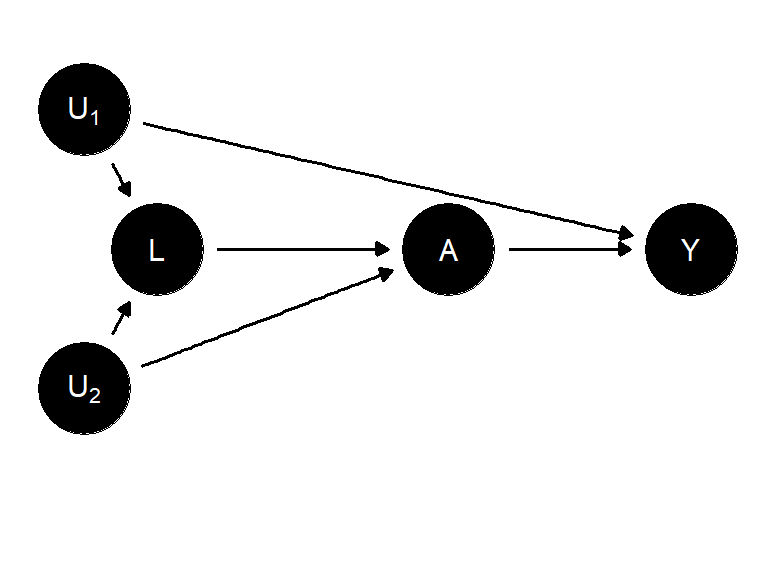
\(L\rightarrow A\) 의 경로를 포함하는 위의 인과 다이어그램에서, 이 경로의 포함은 \(A\leftarrow L \leftarrow U_1 \rightarrow Y\) 라는 뒷문 경로를 개방한다. 왜냐하면 \(U_1\) 가 \(A, Y\) 의 공통 원인이므로 중첩이 존재하기 때문이다. 따라서 여기에서 편향성은 다루기 까다롭다. 중첩 경로를 차단하고자 할 경우에 선택 평향 경로를 개방하는 결과로 이어질 수 있다. 주어진 \(L\) 에서 조건부 교환가능성도, 무조건적 교환가능성도 존재하지 않는다. 이 경우에 편향을 해결하기 위한 방법은 (1) \(U_1\)과 \(A\) 또는 \(Y\) 사이의 변수 \(L_1\)을 측정하거나, (2) \(U_2\)와 \(A\) 또는 \(L\) 사이의 변수 \(L_2\)를 측정하는 것이다.
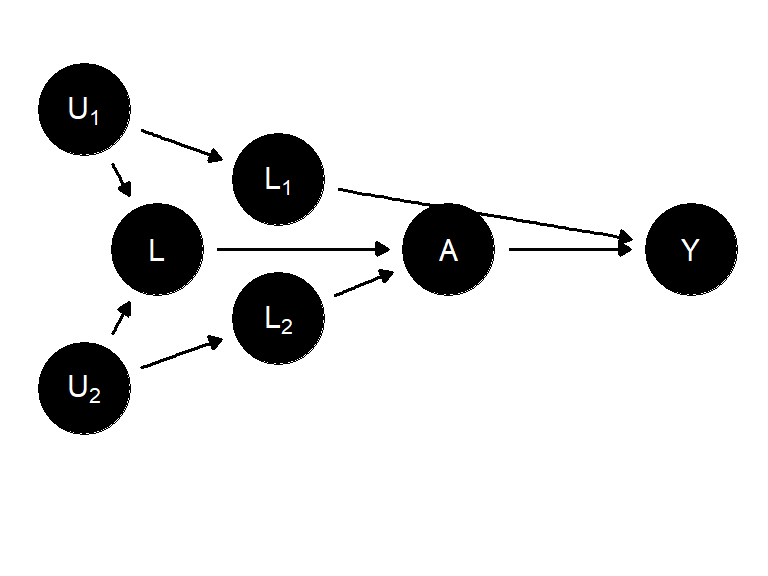
이 챕터에서 다루는 인과 다이어그램들은 처치와 결과 간에 열린 뒷문 경로의 존재로 인하여 교환가능성이 충족되지 않는 두 가지 구조적 상황에 대해서 나타낸다.
- 중첩(confounding): 처치와 결과에 대한 공통 원인이 존재하는 경우로 뒷문 경로가 열리게 된다.
- 선택편향(selection bias): 조건적인 공통효과로, 이전에 차단되었던 뒷문 경로가 어떠한 조건 하에서는 열리는 경우가 존재한다.
7.4 Confounding and confounders
인과 다이어그램을 통해서 단순히 뒷문 기준을 이용해서 어떤 변수를 조정해야하는지를 결정하면 된다. 반면에, 교란인자를 다루기 위한 전통적인 접근법은 대체로 사전적인 인과적 지식보다는 관측된 관계에 기반을 두고 있다.
전통적인 접근 방식에서 교란인자는 (1) 처치와 관련이 있고, (2) 처치에 조건적인 결과와 관련이 있으며, (3) 처치와 결과 사이의 인과적 경로에 있지 않다는 세 가지 조건을 충족하는 변수로 정의된다. 그러나 이러한 전통적인 접근 방식은 부적절한 조정으로 이어질 수 있다. 요컨대, 통제할 경우에 오히려 인과 효과의 선택 편향이 나타날 수 있는데도 불구하고 그저 관찰된 관계를 고려하여 통제 및 조정하려고 하는 경우가 나타날 수 있다는 것이다.
7.5 Single-world intervention graphs
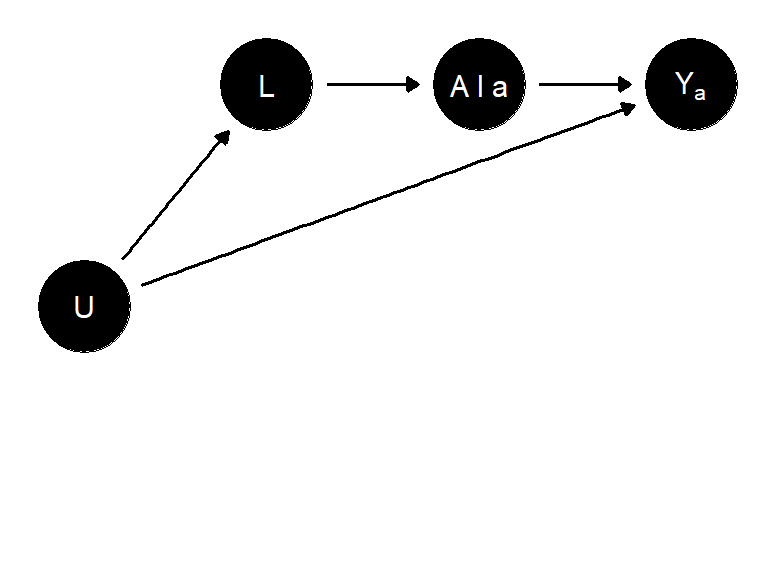
SWIGs는 명시적으로 그래프에 반사실적 변수들을 포함함으로써 반사실적 접근법과 그래프를 이용한 시각화 접근법을 통합하고자 하는 노력이다. 즉, SWIG는 단일한 개입(single intervention)에 의해 만들어진 반사실적 세계를 보여주는 그래프이다.
처치 \(A\) 에 해당하는 노드를 보면,
오른쪽은 개입에 따른 처치 값 \(A\) 를 인코딩하고 원래 인과 관계 DAG에서 \(A\) 에서 벗어난 모든 화살표를 상속한다.
왼쪽은 개입이 없었더라면 관찰되었을 처치 \(A\) 의 값, 즉 처치의 자연스러운 값을 인코딩한다. 개입된 (사실과 반대되는) 세계에서는 인과적 입력이 실제 세계와 동일하기 때문에 인과적 DAG에서 \(A\)에 있던 모든 노드를 상속하게 된다.
SWIG에서 결과는 개입된 세계에서 \(Y\) 의 값인 \(Y_a\) 이며, 나머지 변수는 시간적으로 \(A\) 보다 앞서 있기 때문에 개입의 영향을 받지 않으므로 관찰된 세계에서와 동일한 값을 갖게 된다.
7.6 Confounding adjustment
무작위 배정이 없는 경우, 인과 추론은 \(A\) 로부터 \(Y\) 로 가는 모든 뒷문 경로를 차단하기에 충분한 변수들을 포함하는, 교란 조정을 위해 충분한 일련의 변수 \(L\) 을 측정하였다는 검증할 수 없는 가정에 의존하는 수밖에 없다. 교란인자 \(L\) 을 조정하기 위한 방법은 크게 두 가지로 구분할 수 있다:
G-methods: 표준화, 역확률 가중치, g-estimation과 같이 주어진 \(L\) 하에서 조건부 교환가능성을 추출하여 전체 모집단 혹은 모집단의 일부 서브셋에 대하여 인과 효과를 추정하기 위한 방법이다.
계층화 기반 조정과 같은 전통적인 방법: 계층화와 매칭(matching)으로 \(L\) 에 의해 정의된 서브셋에서 \(A\) 와 \(Y\) 간의 관계를 추정하기 위해 주어진 \(L\) 하에서 조건부 교환가능성을 추출하는 방법이다.
단, 위의 모든 방법은 주어진 \(L\) 하에서의 조건부 교환가능성을 요구한다. 하지만 실제로 우리의 분석 결과의 타당성은 담보되지 않는 경우가 많다.