2 Randomized Experiments
어떤 행동, \(A\)가 우리가 알고 싶어하는 결과에 인과효과를 가지는지, 혹은 그 변화가 우연에 의한 것인지는 어떻게 알 수 있을까? 이를 해결할 수 있는 방법 중 하나가 바로 무작위 실험(randomized experiment)이다. 이 챕터에서는 무작위화(randomization)가 왜 인과추론을 도출해내는지를 설명한다.
2.1 Randomization
앞의 챕터에서 살펴보았듯이 개개인의 처치에 대한 잠재적 결과는 하나만 관측할 수 있다. 즉, 어떤 사람이 처치를 받았을 때의 결과와 다른 사람이 처치를 받지 않았을 때의 결과와 같이 한 사람의 처치에 대한 결과만 확인할 수 있기 때문에 처치를 받은 사람의 처치를 받지 않은 경우는 관측할 수 없게 된다.
무작위 실험은 우리가 관심을 갖고 있는 처치를 제외한 나머지 영향들이 처치를 받는 집단과 받지 않는 집단 모두에게 있어 무작위할 것이라고 간주하게 한다. 즉, 처치를 제외하고 나머지 모든 면에서 처치를 받은 집단(처치군)과 그렇지 않은 집단(통제군)은 서로 교환가능(exchangeability)하다. 그리고 이때, 처치를 받지 않은 경우인 반사실적 결과(counterfactual outcome)는 실제 처치와는 독립적이다: 이상적인 무작위 실험에서는 모든 \(a \in A\)에 대해 \(Y^a \perp\!\!\!\perp A\)라고 할 수 있다.
\(Y^a \perp\!\!\!\perp A\)는 반사실적 결과와 관측된 처치 간의 독립성을 정의한다.
그러나 \(Y^a \perp\!\!\!\perp A\)가 관측된 결과와 관측된 처치 간의 독립성, \(Y \perp\!\!\!\perp A\)을 의미하는 것은 아니다.
이처럼 처치군과 통제군이 서로 교환가능한 조건이라면 처치는 외생적(exogenous)라고 할 수 있다.
무작위 실험은 모집단 또는 평균 인과효과에 관한 내용을 다루고 있다.
2.2 Conditional randomization
어떠한 변수 \(L\)의 값에 대해 조건적인 무작위 확률을 사용하여 무작위 실험을 할 경우, 이를 조건적인 무작위 실험(conditionally randomized experiments)이라고 한다. 앞서의 무작위 실험은 모든 개인에게 공통적이면서 조건적이지 않은 단 하나의 무작위 확률을 사용하였기 때문에 한계 무작위 실험(marginally randomized experiments)라고 한다.
조건적 무작위 실험: 동전 던지기 시 동전 자체의 앞면, 뒷면 확률이 0.75, 0.25로 서로 달라 무작위화가 이 확률에 영향을 받을 때
한계 무작위 실험: 동전 던지기 시 동전의 앞/뒷면 확률이 0.5/0.5로 동일할 경우
조건적 무작위 실험은 처치군과 통제군 간의 교환가능성을 담보하지는 않는다. 따라서 \(Y^a \perp\!\!\!\perp A|L\) 와 같이 \(L\) 의 에 따라 조건적인 교환가능성을 담보한다.
인과효과의 측정지표를 구할 때, 일반적인 한계 무작위 실험에서 조건을 추가해주면 된다: \(\Pr[Y = 1 | A = a]\).
-
조건적 무작위 실험은 서로 다른 두 개의 한계 무작위 실험을 모집단의 서브셋(\(L\) 의 값에 따라)에 따라 결합한 것과 같다.
- 각각의 서브셋에 대해서 평균 인과효과를 구할 수 있다.
- 모집단에 대해서 평균 인과효과를 조건적으로 구하는 방법: \(\Pr[Y^{a=1} = 1]/\Pr[y^{a=0} = 1]\)
2.3 Standardization
\(L\)의 값이 \(l\) 이며, 처치값에 따른 잠재적 결과의 기대값(연속형일 때 평균, 이산형일 때 비율)에 전체 모집단 중 \(L = l\) 일 확률을 곱해서 일종의 가중치를 부여, 표준화하는 것이다.
\[ \sum_l \mathrm{E}[Y|L = l, A = a]\times \Pr[L = l] \]
2.4 Inverse probability weighting
역확률 가중치(inverse probability weighting). 모집단의 모든 개인이 각각 처치를 받지 않았을 때와 처치를 받았을 때 어떤 일이 일어났을지에 대한 시뮬레이션을 생각해보자. 이러한 시뮬레이션은 조건부 교환 가능성 하에서 정확하다. 두 시뮬레이션을 합쳐서 모든 모집단의 개개인이 처치받은 개인과 처치받지 않은 개인으로 나타나는 가상의 모집단을 만들 수 있다. 원래 모집단보다 두 배 더 큰 규모의 이 가상 모집단을 유사 모집단(pseudo-population)이라고 한다.
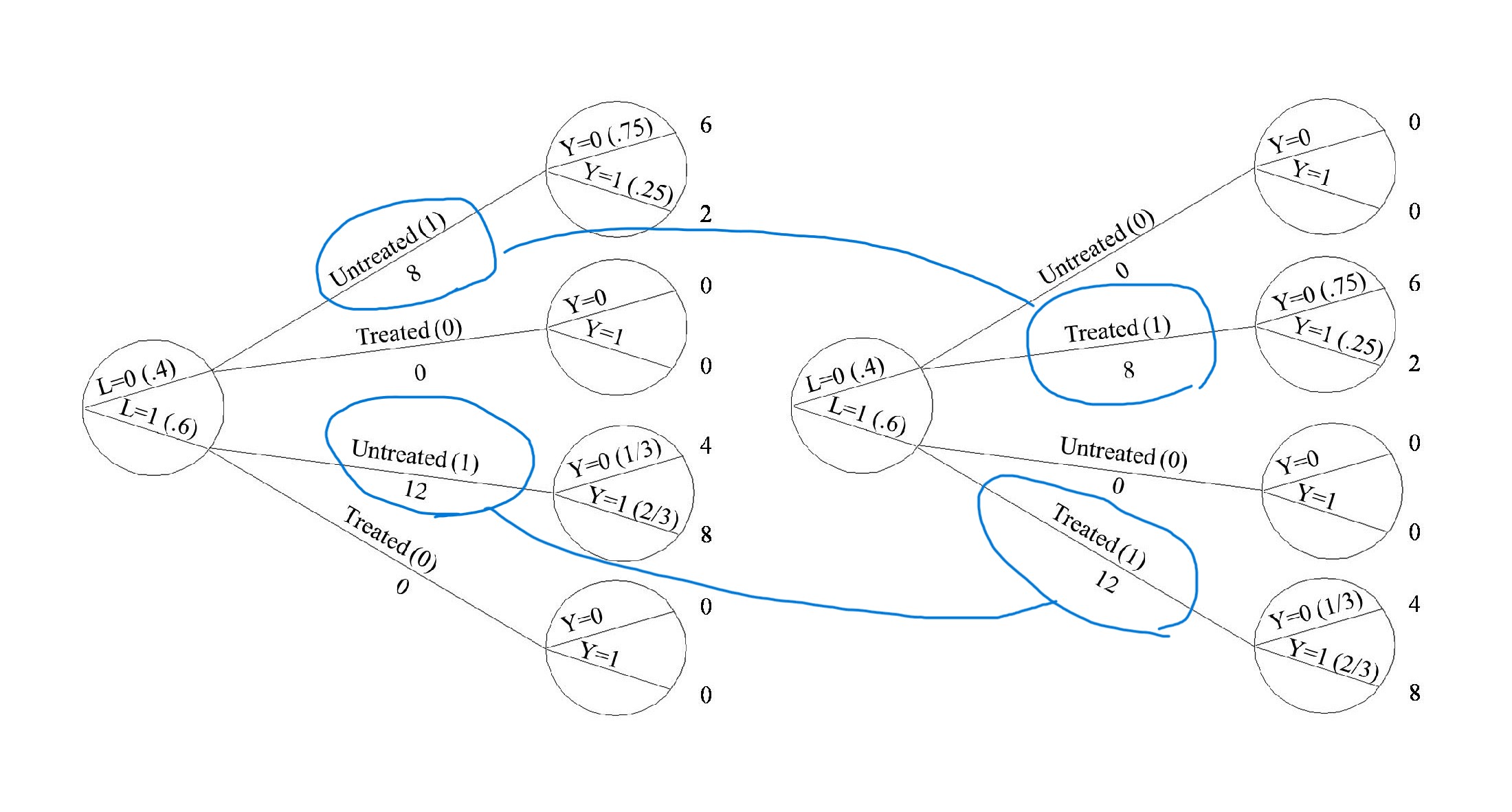
역확률 가중치는 \(W^A = 1/f[A|L]\) 로 나타낼 수 있다.
- 이때, 가중치는 관측된 값이 나타날 확률의 역수(\(1/f[A|L]\))로 계산하여, 나타날 확률이 낮은 관측값에 더 높은 가중치를 부여, 편향성을 낮추는 역할을 수행한다.
역확률 가중치는 표준화와 동일한 결과를 산출한다. 둘은 수리적으로는 동일하기 때문이다.
-
두 방법 모두 개개인이 처치 \(a\) 를 받은 경우를 구성하는 절차라고 볼 수 있다.
역확률 가중치의 경우에는 주어진 공변량 \(L\) 하에서 처치 \(A\) 의 조건부 확률을 사용한다.
표준화는 공변량 \(L\) 의 확률과 주어진 \(A\) 와 \(L\) 에서의 결과 \(Y\) 에 대한 조건부 확률을 사용한다.