1 A Definition of Causal Effect
1.1 Individual causal effects
일반적으로 우리는 어떠한 행동 \(A\)가 이루어졌을 때의 결과와 그렇지 않을 때의 결과를 비교하여, 그 두 결과가 다를 경우 \(A\)가 결과에 대한 인과적 효과(causal effect)를 가진다고 말한다.
개개인에 대한 인과효과에 대한 형식적 정의는 다음과 같다: 처치 \(A\)는 \(Y^{a=1}\neq Y^{a=0}\)이라고 할 때, 개개인의 결과 \(Y\)에 대한 인과효과를 가진다.
즉, \(A\)에 따라 결과가 변해야만 인과효과를 생각해볼 수 있음.
이때, \(A\)의 유무에 따른 결과, \(Y^{a=1}\)와 \(Y^{a=0}\)는 잠재적 결과(potential outcomes)나 반사실적 결과(counterfactual outcomes)라고 함.
개개인에 대한 잠재적 결과들 중 하나(\(Y^A\))는 사실 관측된 결과이다: \(A_i = a\)라고 할 때, \(Y^a_i = Y^A_i = Y_i\)라는 일관성을 갖게 된다.
반면, 그 외의 개개인 수준의 잠재적 결과, \(A_i=0\)인 경우에는 우리는 그 결과를 관측할 수 없으므로 개별 효과는 식별될 수 없다.
-
여기서의 가정은
Stable-unit-treatment-value assumption (SUTVA): 처치 \(A\)에 대한 개개인의 잠재적 결과는 다른 개인의 잠재적 결과에 영향을 받지 않는다는 것이다.
No multiple version of treatment assumption: \(A= a\)라는 단 한 가지 처치만 존재한다.
1.2 Average causal effects
인과효과는 비교할 수 있는 (1) 어떠한 행동(\(A\))의 유무와 그로 인한 (2) 결과(\(Y^{a}\))가 필요하다. 하지만 앞서 말했다시피 개별 수준에서 인과효과를 식별하는 것은 불가능하므로, 집합적 수준(aggregated level)에서의 인과효과에 주목한다.
개개인들의 모집단에서 나타나는 평균적인 인과효과(average causal effect)를 일컫는다.
앞서의 행동과 결과에 이어서 평균 인과효과를 정의하기 위해서는 비교할 결과가 어떤 개개인들로 구성된 모집단인지에 대한 정의가 필요하다.
전체 모집단에 있어서 \(Y^{a=1}\)과 \(Y^{a=0}\)의 평균을 비교할 수 있다.
-
결과에 대한 처치 \(A\)의 평균 인과효과는 \(\Pr[Y^{a=1}=1]\neq\Pr[y^{a = 0}=1]\)일 때 나타난다.
- 모집단 수준에서는 \(\mathrm{E}[Y^{a=1}]\neq\mathrm{E}[y^{a = 0}]\)으로 나타낼 수 있다.
-
평균 인과효과가 나타나지 않는다고 해서 개개인에 대한 효과도 존재하지 않는다는 것은 아니다.
- 단, 개개인들 모두에게서 인과효과가 나타나지 않는다면, 평균 인과효과도 나타나지 않을 것이다.
1.3 Measures of causal effect
인과효과가 없다는 가설(causal null hypothesis)을 보여주는 세 가지 효과 측정지표(effect measures):
Causal risk difference: \(\Pr[Y^{a=1}=1] - \Pr[Y^{a=0}=1]=0\)
Causal risk ratio: \(\frac{\Pr[Y^{a=1}=1]}{\Pr[Y^{a=0}=0]}=1\)
Odds ratio: \(\frac{\Pr[Y^{a=1}=1]/\Pr[Y^{a=1}=0]}{\Pr[Y^{a=0}=1]/\Pr[Y^{a=0}=0]}=1\)
1.4 Random variability
실제로 우리는 모집단의 매우 일부에 해당하는 표본에 대한 정보만을 수집할 수 있다.
우리가 모집단에 속한 개개인들에 대해 정확하게 얻을 수 있는 정보는 \(a\) 라고 하는 처치를 받은 이들의 결과에 대한 비율뿐이며, 처치를 받지 않은 이들의 잠재적 결과에 대해서는 알 수 없다.
따라서 우리는그 (모집단에서의) 확률(probability)을 추정할 수밖에 없다.
모집단으로부터 무작위 표본을 추출했다고 해보자.
표본을 가지고 살펴본 처치를 받지 않았으나 죽은 이들의 비율은 다음과 같이 나타낼 수 있다: \(\widehat{\Pr}[Y^{a=0}] = 1\).
문제는 이 표본의 결과값이 모집단에서의 결과인 \(\Pr[Y^{a=0}] = 1\) 와 정확하게 같을 수는 없다는 것이다.
-
우리는 표본 비율인 \(\widehat{\Pr}[Y^{a=0}] = 1\) 를 사용하여 처치 \(a\) 일 때의 모집단에서의 확률 \(\Pr[Y^{a=0}] = 1\) 를 추정하게 된다.
표본의 크기가 커질수록, 표본 비율과 모비율의 차이는 더 작아지게 된다.
모집단과 표본에서의 차이는 표집 변동성(sampling variability)으로 인한 것일 수 있다.
-
실질적으로 모집단에서의 비율을 얻을 수가 없기 때문에 표본에서의 비율을 가지고 인과 효과가 있다 없다를 확신할 수 없다.
- 인과적으로 효과가 없다는 가설을 평가할 수 있을 뿐이다.
-
표집 변동성 외에도 모집단 비율과 표본의 비율에 차이가 존재할 수 있다.
표본 수준에서 처치에 대한 잠재적 결과가 확률로 나타날 경우이다.
개개인에 대한 인과 효과는 정해진 관측값을 확인할 수 있지만, 이를 평균적인 수준에서 살펴보게 되면 개개인 간의 차이가 존재할 수 있다.
인과추론에서 확률오차는 표집 변동성, 단정적이지 않은 반사실적 사실들, 또는 둘 모두로 인한 것일 수 있다.
1.5 Causation versus association
앞서도 언급했다시피 실제로는 우리는 잠재적 결과(처치된 경우와 처치받지 못한 경우) 중 한 가지의 결과만을 관측할 수 있다. 그래서 우리는 전체 모집단(혹은 우리가 가진 표본) 중에서 처치값(treatment value) \(a\) 를 받은 개개인들 간의 결과, \(Y\) 의 비율(결과가 이산형일 때) 또는 평균(결과가 연속형일 때)을 구해서 살펴보게 된다: \(\Pr[Y = 1|A = a]\).
- 만약 처치를 받았을 때와 받지 않았을 때의 결과가 동일하다면, 처치 \(A\) 는 결과와 관계가 없는, 독립적이라고 할 수 있으며 이 경우에는 \(A \perp\!\!\!\perp Y\) 또는 \(Y \perp\!\!\!\perp A\) 라고 표현할 수 있다.
- 처치를 받았을 때와 받지 않았을 때의 결과의 비율이 같지 않을 때, \(\Pr[Y = 1|A = 1]\neq \Pr[Y = 1|A = 0]\) , \(A\) 와 \(Y\) 는 서로 종속적(dependent)이라고 할 수 있다.
-
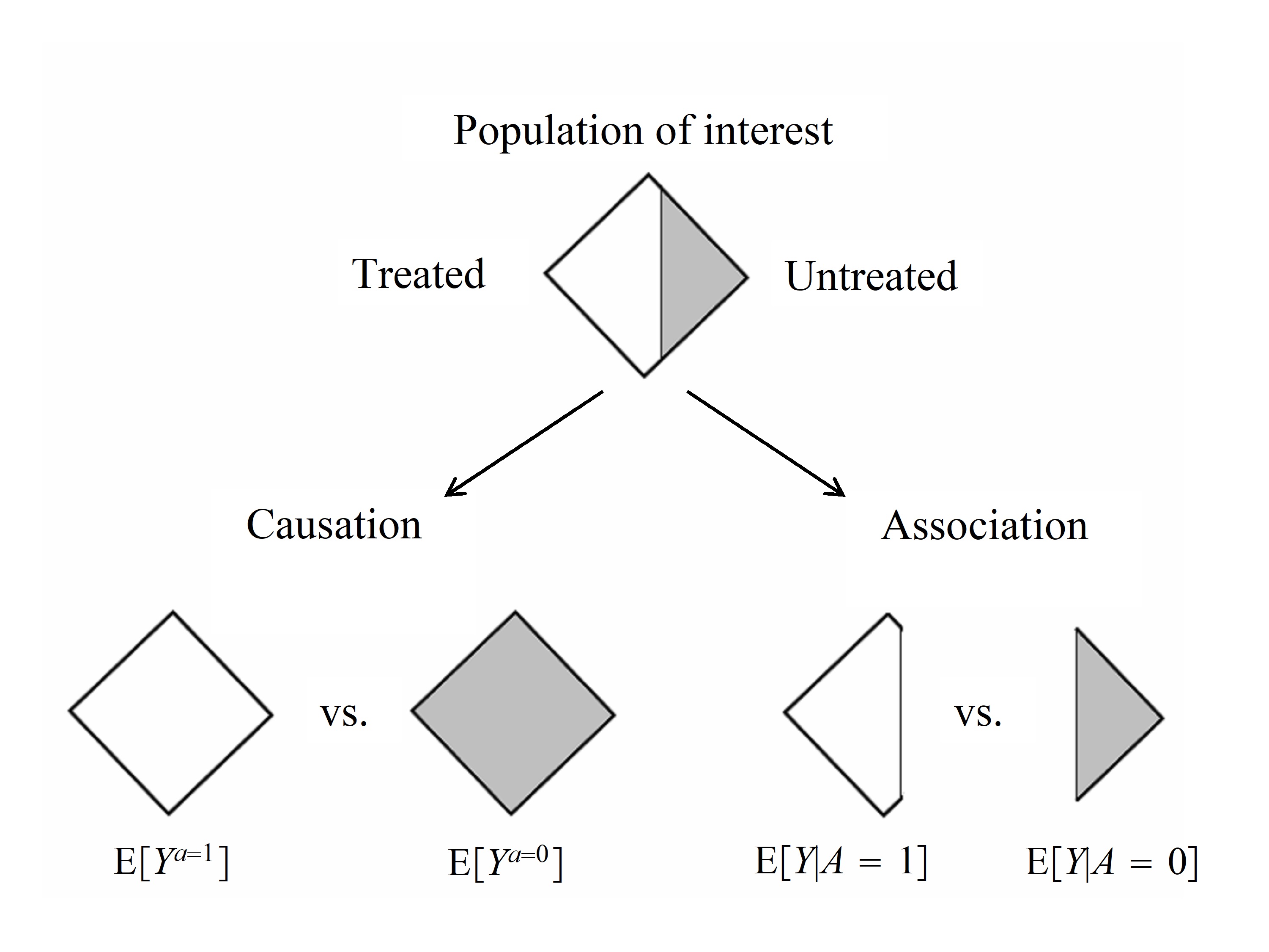
인과관계(causation)의 정의는 전체 하얀색 다이아몬드(처치된 모든 개체)와 전체 회색 다이아몬드(처치되지 않은 모든 개체) 사이의 비교를 의미한다.
- 인과관계는 같은 모집단에서 서로 다른 두 처치 상태(처치 받은 경우와 받지 않은 경우)에서 나타나는 서로 다른 위험도를 보여주는 것이다.
-
연관성(association)은 원래 다이아몬드의 흰색(처리된 부분)과 회색(처리되지 않은 부분) 사이의 비교를 의미합니다.
- 상관성은 처치를 받은 개인들과 받지 않은 개인들이라는 서로 독립적인 모집단의 서브셋에서 나타나는 위험도의 차이를 보여주는 것이다.
인과관계에 대한 질문은 “What if”에 관한 것:”모든 사람들이 치료를 받는다면 위험도는 어떻게 될까?”