5 Interaction

인과적 질문들은 때로는 둘 이상의 처치가 동시에 나타나고 그에 따른 효과에 관한 것일 수 있다. 만약 어떤 처치가 주어진 조건이 달라졌을 때, 인과 효과가 서로 다르게 나타난다고 한다면, 두 처치는 결과에 상호작용 효과를 가진다고 할 수 있다. 둘 이상의 처치에 대한 결합간섭(joint intervention)이 존재한다면, 상호작용의 식별은 가장 효과적인 간섭을 시행할 수 있게 한다.

5.1 Interaction requires a joint intervention

처치 \(E\)와 \(A\)가 동시에 이루어졌다고 하자. 일반적으로 개별 반사실적 결과 \(Y^{a, e}\)는 개인의 \(A\)와 \(E\)의 값이 \(a\)와 \(e\)로 설정했더라면 관찰되었을 결과를 의미한다.

둘 이상의 처치에 대한 간섭을 결합 간섭이라고 한다.
\(E = 1\) 이라고 설정된 결합 간섭 이후의 \(Y\)에 대한 \(A\) 의 인과효과가 \(E=0\) 이라고 설정한 인과효과와 다를 경우에 우리는 두 처치 \(A\) 와 \(E\) 간에 상호작용이 존재한다고 간주한다.
위험도 차이의 척도로 이 상호작용을 나타낸다면, 모집단 수준에서 가산적 척도(additive scale)로 \(A\)와 \(E\) 사이의 상호작용이 존재한다고 나타낼 수 있다.

\[ \begin{aligned} \Pr[Y{a=1,e=1}=1]&-\Pr[Y^{a=0,e=1}=1]\neq\\& \Pr[Y{a=1,e=0}=1]-\Pr[Y^{a=0,e=0}=1] \end{aligned} \]

좌변과 우변이 일치하지 않는다는 것은 처치 \(A\)와 \(E\) 가 상호작용의 정의에 따라 동등한 위상을 가진다는 것을 의미한다.

그렇다면 상호작용과 효과 수정(effect modification) 간의 차이는 무엇일까?

만약 어떤 변수 \(V\) 가 \(Y\)에 대한 \(A\) 효과의 수정인자라고 한다면, \(Y\)의 \(A\) 에 대한 평균 인과효과는 \(V\) 의 수준에 따라 달라진다.
- 여기서 중요한 것은 효과 수정의 핵심은 \(A\) 의 인과효과이지 \(V\) 의 인과효과가 아니라는 것이다.
- 따라서 효과 수정에서는 반사실적 결과가 \(Y^{a, v}\) 가 아니라 \(Y^a|v\) 에 관한 것이다.
상호작용에서는 \(A\) 와 \(E\) 가 동일한 위상을 가진 처치(treatment)이다.
- 상호작용이란 두 개의 처치, \(A\) 와 \(E\) 의 결합 인과효과를 의미하며, 결합 간섭 하에서의 반사실적 결과 \(Y^{a, e}\) 에 관한 것이다.

5.2 Identifying interaction

상호작용은 두 개 이상의 처치의 결합효과로 간주되기 때문에 상호작용을 식별하기 위해서는 교환가능성, 양의 확률, 그리고 일관성이 두 효과 모두에 요구된다.

처치 \(E\) 가 무작위로 배정된다면, 상호작용과 효과 수정의 개념은 동일하다.
- 효과 수정은 \(V\) 가 무작위로 배정된 것이 아니고, 그에 따라 \(V\) 의 수준별로 상이한 처치의 인과효과가 나타날 수 있다고 보는 것이기 때문에.
처치 \(E\) 가 연구자에 의해 배정되지 않았다고 가정해 보자. \(A\)와 \(E\) 간의 상호작용의 존재를 평가하기 위해서는 여전히 \(\Pr[Y^{a, e} = 1]\) 의 네 가지 한계 위험도를 추정해야 한다.
- \(A\)와 \(E\) 를 서로 다른 처치로 구분하는 것이 아니라 \(AE\) 라는 결합된 처치로 간주할 수 있다.
- 만약 \(A\) 에 대해서는 (조건적) 교환가능성을 가정할 수 있는 반면에 \(E\)에 대해서는 가정할 수 없다면, \(A\)와 \(E\) 간의 상호작용의 존재를 평가하기는 어렵지만 \(E\)에 의한 효과 수정의 존재 가능성에 대해서는 평가할 수 있다.
- 단, \(V\) 와 \(E\) 의 차이는 \(V\) 의 경우 \(Y\) 에 영향을 미칠 수 있으며 \(A\) 와 상호작용하는 식별되지 않은 변수들과 상관관계를 가질 수 있다는 것이다.

5.3 Counterfactual response types and interaction

처치 \(E\) 가 존재할 때, 처치 \(A\) 인과효과는 \(\Pr[Y{a=1, e=1} =1] - \Pr[Y^{a=0, e=1} = 1]\) 로 나타낼 수 있으며, 이 인과효과는 처치 \(E\) 가 존재하지 않을 때의 인과효과 \(\Pr[Y{a=1, e=0} =1] - \Pr[Y^{a=0, e=0} = 1]\) 과 같다.

처치 \(A\) 와 \(E\) 간에 상호작용이 존재한다는 것은 \(A = a\) 일 때의 반사실적 결과는 \(E\) 의 값에 대한 정보 없이는 온전히 이해될 수 없고, 그 반대의 경우도 그러하다는 것을 의미한다. 따라서 상호작용을 이해하기 위해서는 세 가지 경우의 수가 필요하다:

두 개의 이산형 처치가 있다고 할 때, 가능한 네 개의 처치 조합(treatment combinations)에서 한 가지 조합에 따른 결과만 가지는 경우의 수
두 개의 처치 조합들 중에서 각 처치가 완전히 반대인 경우의 수: \((Y^{a = 1, e = 0} = 1, Y^{a = 0, e= 1} = 1)\) 그리고 \((Y^{a = 1, e = 1} = 1, Y^{a = 0, e = 0} = 1)\).
네 가지 조합의 수 중에서 세 가지 처치가 이루어진 경우의 수.

상호작용은 개개인의 반사실적 응답 유형에 따라서 구분된다.

5.4 Sufficient causes

실제로 처치를 받은 개개인들을 살펴보자. 그 중 몇몇이 죽었다고 할 때, 이는 해당 처치 그 하나로는 결과를 설명하기에는 충분하지 않다는 것을 의미한다.

심장 이식 \(A = 1\) 이 마취제에 알러지가 있는 이들에게만 죽음이라는 결과로 이어졌다고 하자. 이 경우에 심장이식 \(A = 1\) 과 마취제에 대한 알러지 \(U_1 = 1\) 은 결과 \(Y\) 에 대한 최소한의 충분 원인(sufficient cause)이다.

이번에는 처치를 받지 않은 개개인들을 살펴보자. 이들 중 몇몇만이 사망했다고 하면, 처치의 부재만으로 결과를 설명하기에는 충분하지 않다는 것을 의미한다.

처치를 받지 않은 이들 중에서 박출률(ejection fraction, \(U_2 = 1\))이 20% 미만인 경우만 사망하였다고 하자. 이 경우에는 처치의 부재 \(A = 0\) 와 낮은 박출률의 존재 \(U_2 = 1\) 가 결과 \(Y\) 에 대한 또 다른 충분 원인이다.

마지막으로 처치 여부와는 무관하게 \(U_1\) 와 \(U_2\) 모두 없는 데 사망한 개개인들의 경우를 생각해보자.

이는 결과를 설명하기 위해서 필요한 또 다른 배경 요인이 있다는 것을 시사한다.

충분요인원인(sufficient-component causes)는 충분원인과 그 요소들을 일컫는다.

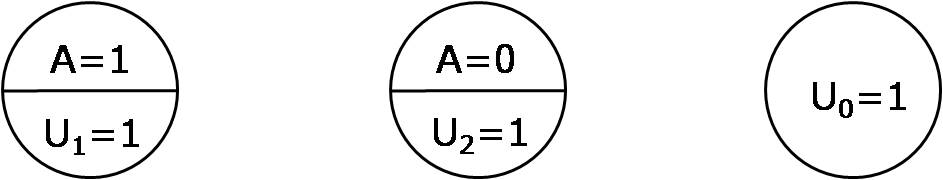
위의 그림은 효과 수정에 대한 핵심적 결과를 시각화한 것이다: 처치 \(A\) 의 인과효과의 크기는 효과 수정인자의 분포에 따라 좌우된다는 것이다.

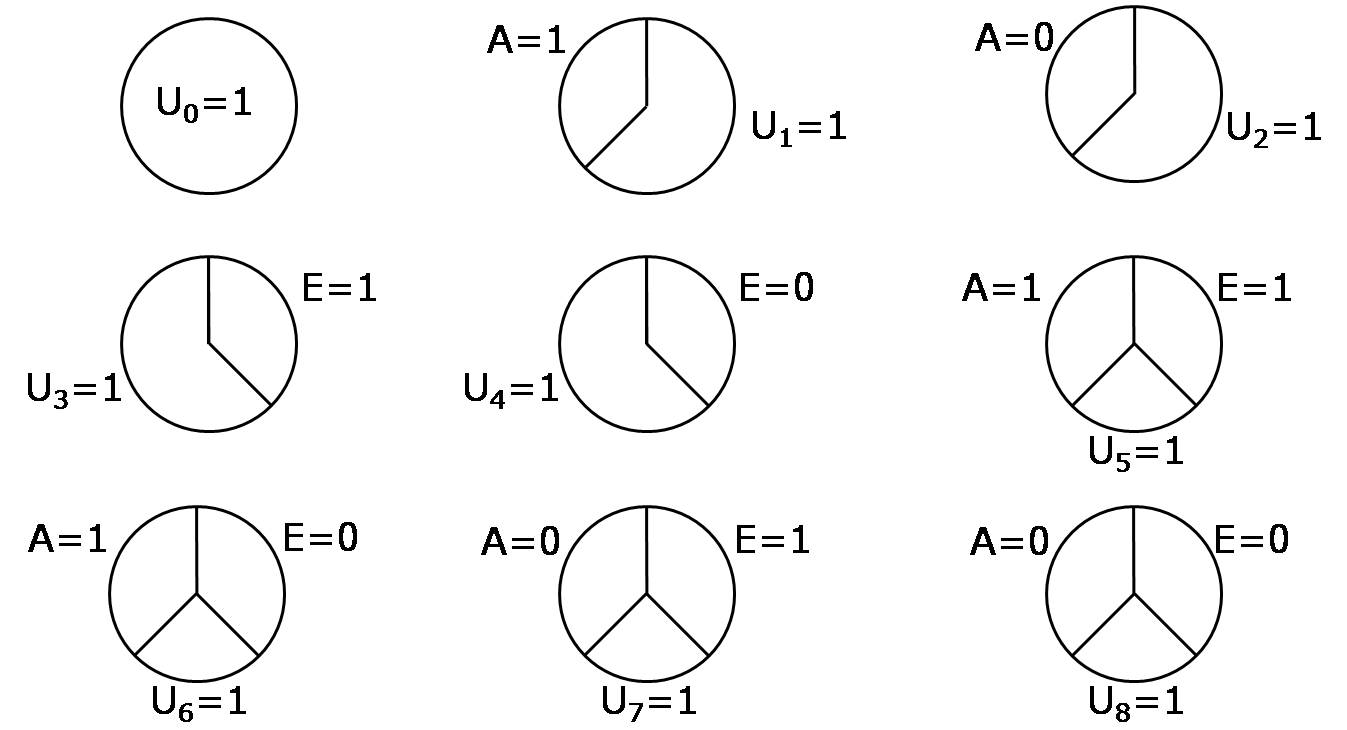
5.5 Sufficient cause interaction

상호작용의 근간이 되는 인과적 메커니즘에 대해 고민할 필요가 없다.

상호작용은 반사실적 결과의 대비로 정의되며, 따라서 교환가능성, 양의 확률 및 일관성의 조건이 처리 \(A\)와 \(E\) 모두에 적용되는 이상적인 무작위 실험을 수행하여 식별할 수 있다.
하지만 상호작용은 충분요인원인의 틀로도 개념화할 수 있다.

상호작용의 반사실적 정의와 달리 충분한 원인 상호작용은 처치 \(A\)와 \(E\)를 포함하는 인과적 메커니즘을 명시적으로 언급한다.

때로는 충분한 원인과 그 구성 요소에 대한 지식이 전혀 없더라도 충분한 원인 상호 작용이 존재한다고 결론을 내릴 수 있다.

5.6 Counterfactuals or sufficient-component causes?

충분요인원인 분석틀과 반사실적 결과 분석틀은 서로 다른 질문을 다룬다.

충분요인원인 분석틀: “특정 효과가 주어졌을 때, 그 원인이 될 수 있는 다양한 사건들에는 어떤 것이 있는가?”
반사실적 결과 분석틀: “특정 요인에 개입하여 실제와 다른 수준으로 설정했다면 어떤 일이 발생했을까?”

충분요인원인 분석틀과 달리 반사실적 결과 분석틀은 요인이 결과에 영향을 미치는 메커니즘에 대한 자세한 지식이 필요하지 않는다.

하지만 이론적 유용성을 떠나서 충분요인원인 분석틀이 실제 데이터 분석에 얼마나 적실한지에 대해서는 아직 검증되지 않았다.

인과 관계를 보다 일반적으로 추정하기 위해서는 반사실적 결과 분석틀이 계속해서 가장 자주 사용될 것으로 기대된다.