6 Graphical Representation of Causal Effects
앞서의 챕터들에서 간단한 인과관계를 살펴보았던 것과는 달리, 보다 복잡한 관계를 살펴보기 위해서는 특정한 인과 추론에 관한 문제들에 적절한 변수들에 대한 가정과 우리가 알고 있는 것들을 명시적으로 드러내는 것이 필요하다. 이 챕터에서는 우리가 관심을 가지고 잇는 인과 구조에 대한 질적인 전문적 지식과 사전 가정들을 시각적으로 나타내는 도구에 대해 소개한다.
6.1 Causal diagrams
인과 다이어그램은 핵심적인 인과 개념들을 나타내는 데 사용되는 시각화 도구이다.
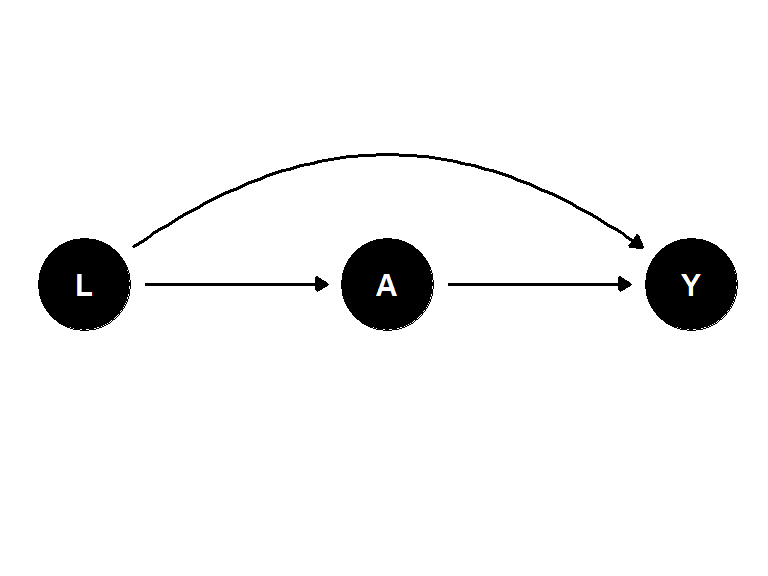
확률변수 \((L, A, Y)\)와 이 노드들을 잇는 엣지(화살표)가 있다고 하자. 이때, 시간이 화살표에 따라 좌에서 우로 따르고 \(L\) 이 시간적으로 \(A\) 와 \(Y\) 에 선행하며, \(A\) 는 시간적으로 \(Y\) 에 선행한다고 하자.
이때 화살표는 직접적 인과 효과를 의미한다.
다만, 이때 우리는 효과의 방향성에 대해서는 고려하지 않는다.
이러한 인과 다이어그램을 유향 비순환 그래프 (Directed acyclic graph)라고 하며 줄여서 DAGs 라고 한다. 비순환이라고 하는 이유는 화살표가 한쪽으로만 흐르고 있기 때문이다.
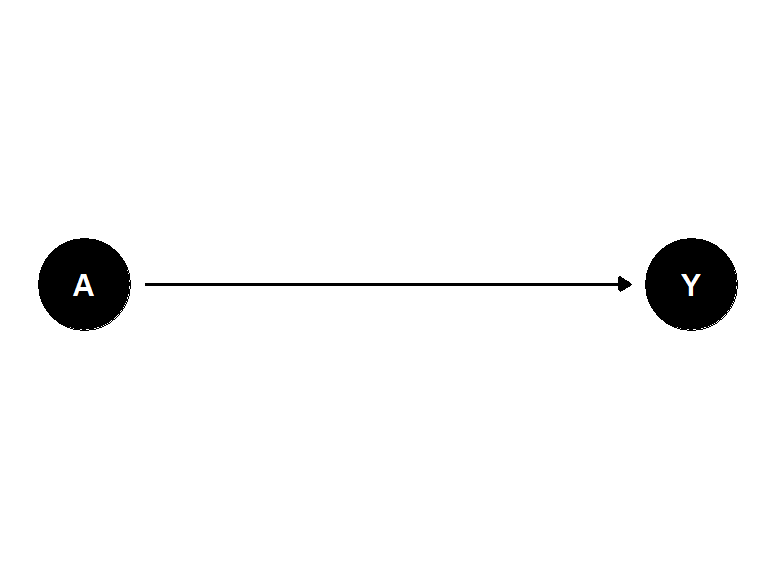
앞서 \((L, A, Y)\)의 인과 다이어그램이 조건부 무작위 실험 또는 관측 연구를 나타냈다면, \((A, Y)\) 의 인과 다이어그램은 한계무작위 실험을 나타낸다.
6.2 Causal diagrams and marginal independence
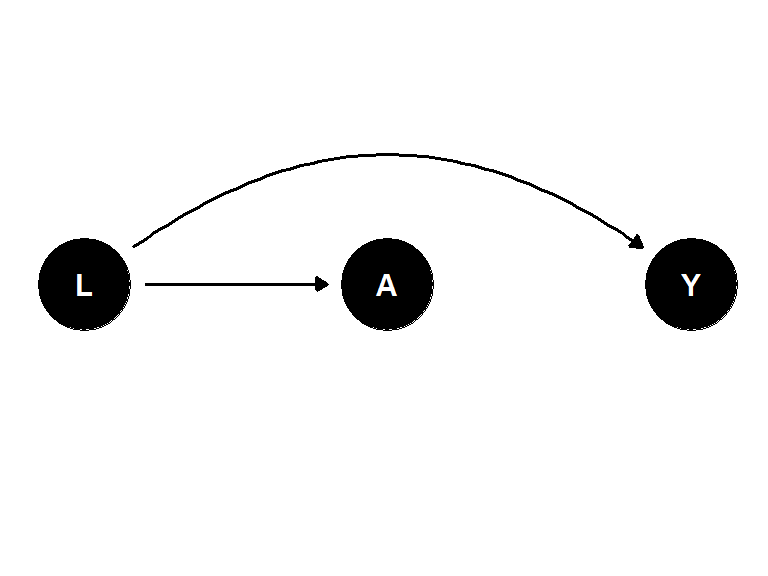
\(L\) 과 \(A\) 와 \(Y\) 의 공통원인인 경우도 나타낼 수 있다.
- 이러한 관계를 그리기 위해서는 단지 인과관계에 대한 지식만이 필요하다.
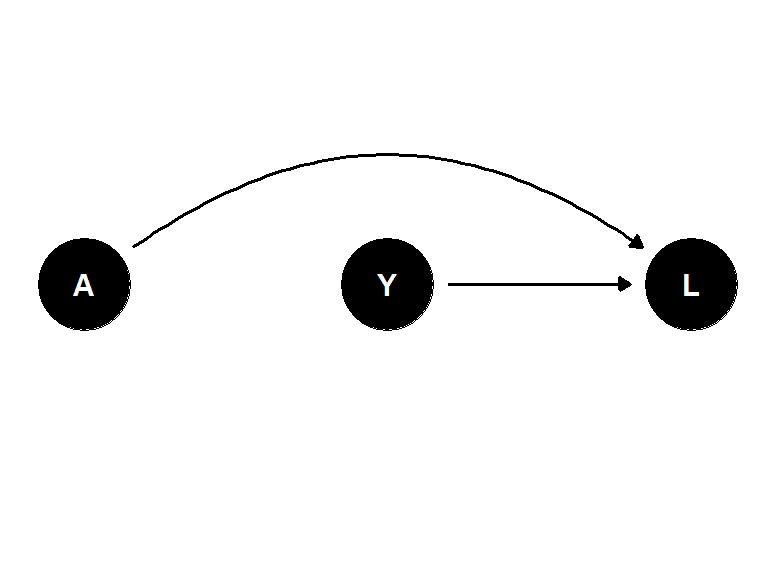
위의 인과관계 다이어그램은 \(A\) 와 \(Y\) 사이에 인과적 관계가 존재하지 않으며, \(L\)은 \(A\)와 \(Y\)의 공통 효과로 묘사되어 있다. 이 노드에서 두 개의 화살촉이 충돌하기 때문에 공통 효과 \(L\)을 \(A \rightarrow L \leftarrow Y\) 경로의 충돌인자(collider)라고 한다.
- \(A\)와 \(Y\)는 둘 사이의 유일한 경로가 충돌인자 \(L\)에 의해 차단되기 때문에 독립적이다.
6.3 Causal diagrams and conditional independence
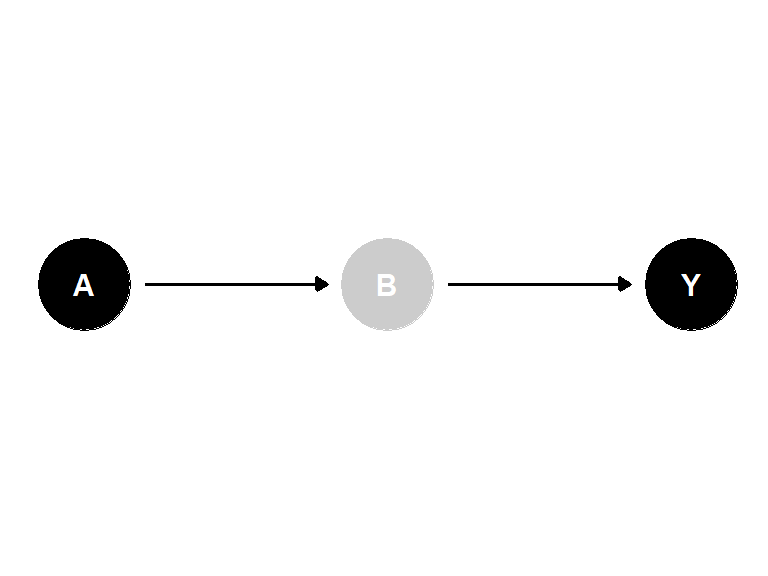
\(A\) 와 \(Y\) 간의 인과효과는 \(B\) 라는 매개인자에 의해 매개될 수 있다.
이 경우, \(B\) 가 주어졌을 때, \(A\) 와 \(Y\) 는 서로 독립적이라는 것을 의미한다.
\(B\) 는 \(A\) 로부터 \(Y\) 로 이루어지는 효과를 막고 있다.
6.4 Positivity and consistency in causal diagrams
종종 다른 노드들에 비해서 처치 노드의 인과관계에서의 다른 위상을 명시적으로 보여주기 위해서 결정 노드(decision nodes)라는 것을 인과 다이어그램에 포함하기도 한다. 인과 다이어그램에서 처치 변수에 대한 노드는 충분히 잘 정의된 개입에 대응될 필요가 있다.
관심 있는 개입에 대해 명시적으로 나타내는 것은 인과 관계를 잘 정의하고, 관련 데이터를 식별하고, 조정 변수(adjustment variables)를 선택하는 데 중요한 단계이다.
6.5 A structural classification of bias
체계적 편향(systematic bias)는 한정된 표본 크기에서 인과효과를 식별하는 데 충분하지 안은 데이터를 가지고 있을 때 나타난다고 한다. 하지만 보다 이론적으로는 처치와 결과 간에 모집단 수준에서의 결과에 대한 처치의 인과효과가 나타나지 않을 수 있는 구조적 관계가 존재할 경우, 이를 체계적 편향이라고 한다.
편향이 존재하지 않는다고 하는 것은 모집단에서의 관계 측정지표가 모집단에서의 대응되는 효과 측정지표와 일관된다는 것을 의미한다.
또한 교환가능성이 없는 경우도 편향으로 이어진다.
편향으로 이어질 수 있는 두 가지 요인:
- 관계 측정지표가 효과 측정지표와 다를 때, 혼재(confounding)에 따른 편향
- 공통 효과에 대한 조건이 존재할 때, 효과없음에 대한 선택적 편향(selection bias)
- 어렵게 생각할 것은 아니고 처치와 결과 간의 관계에 영향을 미치는 조건이 존재하는 데, 이를 간과할 경우에 나타날 수 있는 편
6.6 The structure of effect modification
인과 관계 다이어그램은 \(A\)와 \(V\)가 모두 사망 \(Y\)에 영향을 미친다는 것을 암시하지만, \(V\)가 \(A\)가 \(Y\)에 미치는 영향을 수정할 수 있는 다음의 세 가지 질적으로 구별되는 방식을 구분하지는 않는다:
처치 \(A\)가 사망률 \(Y\)에 미치는 인과적 영향은 두 계층 \(V = 1\)과 계층 \(V = 0\) 모두에서 동일하다.
처치 \(A\)가 사망률 \(Y\)에 미치는 인과적 효과의 방향은 계층 \(V = 1\)과 계층 \(V = 0\) 에서 서로 반대이다(질적 효과 수정).
처치 \(A\)는 \(V\)의 한 계층에서는 \(Y\)에 인과적 영향을 미치지만 다른 층위에서는 인과적 효과가 없다.
즉, 유효한 인과 그래프는 \(V\)에 의한 위의 세 가지 다른 정성적 유형의 효과 수정을 구분하지 못한다.
인과 다이어그램은 원칙적으로 두 처치 \(A\)와 \(E\) 사이의 상호작용 존재 여부에 대해 무관하지만, 인과 다이어그램은 충분 구성 요소를 나타내는 노드(5장 참조), 즉 처치에서 충분요인원인으로 향하는 결정적 화살표가 있는 노드를 추가하여 보강할 경우 상호작용에 대한 정보를 인코딩할 수 있다.