Chapter 12 Transformations and regression

데이터를 원 자료 그대로 회귀모델에 적합하는 것이 항상 최선인 것은 아니다. 따라서 데이터를 어떤 식으로든 변형을 해주는 작업이 요구될 수 있는데, 이러한 변환은 실제 적용에 있어서 회귀모델의 구축과 비교에 대해 보다 일반적인 접근이 가능하게 하며, 더 많은 사례들을 설명할 수 있도록 한다.

12.1 Linear transformations

12.1.1 Scaling of predictors and regression coefficients

계수 $\beta_j$는 다른 예측변수들이 모두 일정할 때, $j$번째 예측변수의 한 단위 변화에 따라 $y$의 평균적인 변화가 어떠한지를 나타낸다. 하지만 때로 $x$의 한 단위 증가라는 것이 적절한 비교를 보여주지 못할 수 있다.

\[ \text{earnings} = −85 000 + 1600 ∗ \text{height} + \text{error}, \]

선형모델은 이 문제를 풀기에 가장 적절한 방법이라고 보기에는 힘들다. 왜냐하면 이 결과를 곧이곧대로 해석하게 된다면 우리는 절편값 -85,000을 키가 0인 사람의 예측 소득이라고 이해해야 하기 때문이다.

하지만 모델의 형태를 조금 바꾸어보면 어떻게 될까?

\[ \begin{aligned} &\text{earnings} = −85 000 + 63 \times \text{height (in millimeters)} + \text{error},\\ &\text{earnings} = −85 000 + 101 000 000 \times \text{height (in miles)} + \text{error}. \end{aligned} \]

자, 이제는 키가 얼마나 중요한 요인인가? $63은 그다지 중요해보이지 않지만 $101000000은 매우 커 보인다. 일견 달라보이는 이 두 수식은 앞선 모델과 똑같은 정보를 내포하고 있다.

선형관계를 유지한 채로 예측변수와 결과변수에 변형을 가하는 것은 예측 결과나 모델 적합에 영향을 미치지 않는다. Gelman, Hill, and Vehtari (2020, 184) 참고.

12.1.2 Standardization using z-scores

계수값의 척도를 조정하는 작업, 스케일링(scaling)에는 또 다른 방법이 있는데, 바로 예측변수로부터 평균을 빼고 표준편차로 나누어주는 이른바 표준화(standardize)하여 “z-score”를 계산하는 것이다. 이 경우 표준화된 예측변수의 계수값은 예측변수의 표준편차에 따른 변화로 해석할 수 있다.

표준편차는 일종의 실질적인 유의성을 가진 측정지표라는 점에서 유용하다.
- 예측변수의 1 표준편차 변화는 평균과 무작위로 뽑은 관측치 사이의 차이를 대략적으로 반영하고 있는, 유의미한 차이이기 때문이다.
예측변수를 z-scores를 이용해 표준화하는 것은 절편의 해석은 모든 예측변수의 값을 평균에 고정하였을 때의 $y$의 평균으로 바뀌게 된다(원래는 다른 모든 값이 0일 때 $y$의 평균).

예측변수의 표본평균과 표준편차를 이용하여 표준화를 하는 것은 관측치의 수가 충분히 담보되었을 때에야 그 추정량의 안정성을 확보할 수 있다. Gelman, Hill, and Vehtari (2020, 184) 는 표본의 규모가 작을 때에는 모집단 분포를 특정하거나 다른 합당한 스케일에 따라서 표준화를 할 것을 추천하고 있다.

어찌보면 당연한게, 표본의 규모가 작을수록 그 분포는 매우 치우칠(skewed) 가능성이 크고 편차가 크게 나타날 가능성이 높으므로 표준화가 유용하지 않을 수 있다.
아니, 그 경우에는 통계적 접근 자체가 유용하지 않을 수도.

12.1.3 Standardization using an externally specified population distribution

데이터 밖의 기준을 바탕으로 스케일링을 하는 접근법에 대해서도 알아보자. 예를 들어, 시험 성적을 분석할 때, 성적을 내야 하는 모든 학생들을 대상으로 시험 성적의 표준편차로 스케일링을 해서 추정량을 나타내는 것이 일반적이다. 시험이 0-100점 척도라고 한다면, 4학년의 전국 평균이 평균 55에 표준편차 18이라고 하자. 그렇다면 개별 학교의 4학년들의 시험 성적도 그 전국 기준에 맞추어서 스케일링을 하는 것이다. 단순하게 얘기하면 모의고사 보면 전국편차 나오는 것과 같다. 개별 학교들이 표본이겠지만(각 학교가 접근할 수 있는 데이터), 스케일링은 전국 단위의 외부 데이터를 바탕으로 이루어지는 것이다. 이같이 고정된 값으로 스케일링을 할 경우에 개별 데이터셋을 따로따로 표준화하는 것보다 더 직접적으로 추정량을 비교할 수 있다는 장점이 있다.

12.1.4 Standardization using reasonable scales

단위에 따라서 예측변수를 조정하거나 리스케일링하는 것도 계수값을 이해하는 데 도움을 준다. 예를 들어, 소득을 $10,000 단위로 설정한다거나, 나이를 10년 씩 구분해주는 것 등이다.

12.2 Centering and standardizing for models with interactions

중심화(centering)은 예측변수의 평균을 뺀 값을 대체변수로 이용하는 접근법이다. 엄마의 IQ와 고등학교 졸업 여부, 그리고 그 상호작용이 아이의 시험성적에 미치는 영향을 보는 예제를 다시 떠올려보자.

그 예제를 원변수 그대로 분석한다면 각각 다른 예측변수가 고정되어 있을 때, 엄마가 졸업했는지 여부에 따른 아이의 시험성적 차이나 혹은 엄마의 IQ에 따른 아이의 시험성적 차이를 확인할 수 있다.
- 하지만 mom_iq = 0, 엄마의 IQ가 0일 때 아이 엄마의 고등학교 졸업 여부가 아이의 시험성적에 미치는 영향을 본다는 것은 실질적으로 의미가 없다. 왜냐하면 IQ가 0인 엄마를 실제로 찾아볼 수 없기 때문이다.
- 때문에 그 예제에서 mom_iq의 계수값 0.9라는 결과도 해석이 와닿지 않는다. 왜냐하면 그 기울기란 결국 엄마가 mom_hs=0인 아이들에 대한 주효과(main effect)이기 때문이다. 그러나 mom_hs = 0이란 데이터의 끝단에 위치한 극단적인 값이기 때문에 그로부터 얻은 계수값을 전체 모집단에 대한 평균으로 해석할 수는 없다.

fit_kid <- stan_glm(kid_score ~ mom_hs + mom_iq + 
                      mom_hs:mom_iq, data = kidiq, refresh = 0)
print(fit_kid)

## stan_glm
##  family:       gaussian [identity]
##  formula:      kid_score ~ mom_hs + mom_iq + mom_hs:mom_iq
##  observations: 434
##  predictors:   4
## ------
##               Median MAD_SD
## (Intercept)   -10.9   13.0 
## mom_hs         50.3   14.9 
## mom_iq          1.0    0.1 
## mom_hs:mom_iq  -0.5    0.2 
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 18.0    0.6  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

12.2.1 Centering by subtracting the mean of the data

그렇다면 투입된 예측변수들로부터 평균을 빼고 다시 회귀분석을 수행한 뒤 해석해보자.

kidiq$c_mom_hs <- kidiq$mom_hs - mean(kidiq$mom_hs)
kidiq$c_mom_iq <- kidiq$mom_iq - mean(kidiq$mom_iq)

이 경우 각각의 주효과(상호작용이 아닌)는 다른 변수의 평균값이 고정되어 있는 상태에서의 예측 차이를 보여주게 된다:

fit_kid_c <- stan_glm(kid_score ~ c_mom_hs + c_mom_iq + 
                      c_mom_hs:c_mom_iq, data = kidiq, refresh = 0)
print(fit_kid_c)

## stan_glm
##  family:       gaussian [identity]
##  formula:      kid_score ~ c_mom_hs + c_mom_iq + c_mom_hs:c_mom_iq
##  observations: 434
##  predictors:   4
## ------
##                   Median MAD_SD
## (Intercept)       87.6    0.9  
## c_mom_hs           2.8    2.4  
## c_mom_iq           0.6    0.1  
## c_mom_hs:c_mom_iq -0.5    0.2  
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 18.0    0.6  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

하지만 모델 자체의 함의는 변한 것이 없기 때문에 잔차의 표준편차는 변하지 않는다. 예측변수들의 선형변환은 모델의 적합도에 영향을 미치지 않는다. 상호작용에 대한 계수값과 표준오차도 변하지 않는다. 변하는 것은 단지 주효과와 절편값일 뿐이고, 이들은 각기 데이터의 평균에 비교하여 해석할 수 있게 된다.

12.2.2 Using a conventional centering point

중심화를 하는 또 하나의 선택지는 바로 mom_hs의 범주의 중간 지점이나 모집단 평균 IQ와 같은 납득할 수 있는 기준점을 이용하는 것이다.

kidiq$c2_mom_hs <- kidiq$mom_hs - 0.5
kidiq$c2_mom_iq <- kidiq$mom_iq - 100

여기에서 c2_mom_hs는 mom_iq = 100인 아이들 중에서 mom_hs = 1인 아이와 mom_hs = 0인 아이 사이의 평균 예측 차이를 보여준다. 마찬가지로 c2_mom_iq는 mom_hs=0.5인 조건에서의 아이들 성적의 예측차이를 보여준다.

12.2.3 Standardizing by subtracting the mean and dividing by 2 standard deviations

중심화는 회귀모델에서 주효과를 해석하는 데 도움을 주지만 여전히 스케일링의 문제는 남아있다. mom_hs의 계수값은 mom_iq보다 훨씬 더 크기 때문에 우리가 각 변수들의 효과를 다른 변수와 비교해서 설명하기가 어렵다는 것이다.

Gelman, Hill, and Vehtari (2020, 186) 은 예측변수들을 2 표준편차로 나누어주는 표준화에 대해서 제안한다. 왜냐하면 그렇게 표준화할 경우 리스케일링된 예측변수의 한 단위 변화는 평균으로부터 위로 1 표준편차, 아래로 1표준편차에 따른 차이를 보여줄 수 있기 때문이다.

kidiq$z_mom_hs <- (kidiq$mom_hs - mean(kidiq$mom_hs))/(2*sd(kidiq$mom_hs))
kidiq$z_mom_iq <- (kidiq$mom_iq - mean(kidiq$mom_iq))/(2*sd(kidiq$mom_iq))

이제 우리는 계수값을 거의 동일한 척도 선상에서 해석할 수 있게 된다.

fit_kid_c2 <- stan_glm(kid_score ~ z_mom_hs + z_mom_iq + 
                      z_mom_hs:z_mom_iq, data = kidiq, refresh = 0)
print(fit_kid_c)

## stan_glm
##  family:       gaussian [identity]
##  formula:      kid_score ~ c_mom_hs + c_mom_iq + c_mom_hs:c_mom_iq
##  observations: 434
##  predictors:   4
## ------
##                   Median MAD_SD
## (Intercept)       87.6    0.9  
## c_mom_hs           2.8    2.4  
## c_mom_iq           0.6    0.1  
## c_mom_hs:c_mom_iq -0.5    0.2  
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 18.0    0.6  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

12.2.4 Why scale by 2 standard deviations?

Gelman, Hill, and Vehtari (2020, 187) 이 1 표준편차가 아니라 2 표준편차로 표준화를 해줄 것을 제안하는 이유는, 2 표준편차로 나누었을 경우에 이항변수로 예측변수를 투입하더라도 일관된 결과를 얻을 수 있기 때문이다.

이항변수 $x$가 있다고 하고, 그 이항변수의 확률이 0.5라고 하자.
이때 $x$의 표준편차는 $\sqrt{0.5\times 0.5} = 0.5$가 되며, 표준화된 변수는 $(x-\mu_x)/(2\sigma_x)$로 나타낼 수 있다. 이는 $\pm 0.5$로 $x=0$일 때와 $x=1$일 때 사이의 계수값 비교를 보여주게 된다.
반면에 1 표준편차로 스케일링을 하게 될 경우에는 $\pm 1$로 계수값은 $x$가 실제로 취할 수 있는 값에 따른 예측 결과의 차이를 절반밖에 보여주지 못하게 된다.

12.2.5 Multiplying each regression coefficient by 2 standard deviations of its predictor

상호작용항이 없는 모델일 경우에 중심화를 하는 것과 변수를 리스케일링을 하는 것은 원자료로 회귀계수를 추정한 뒤 각 $\beta$에 $x$의 2 표준편차를 곱하는 결과와 같다.

12.3 Correlation and “regression to the mean”

단순선형회귀모델 $y = a + bx + \text{error}$가 있다고 하자. 만약 두 $x$와 $y$가 표준화된 변수라면, 즉 x <- (x - mean(x))/sd(x)이고 y <- (y - mean(y))/sd(y)라면, 회귀모델에서 절편은 0이며 기울기는 단순히 $x$와 $y$의 상관관계만을 보여주게 될 것이다.

따라서 두 표준화된 변수의 회귀계수 기울기 값은 반드시 -1과 1 사이에 위치하게 되며, 만약 이 기울기의 절대값이 1을 넘는다면 그것은 $y$의 분산이 $x$의 분산을 초과하기 때문이라고 이해할 수 있다.

일반적으로 하나의 예측변수에 대한 회귀계수의 기울기값은 $b = \rho \sigma_y / \sigma_x$로 나타낼 수 있으며, $rho$는 두 변수 $x$와 $y$의 상관관계이며, $\sigma_x$, $\sigma_y$는 $x$와 $y$의 표준편차이다.

12.3.1 The principal component line and the regression line

아래의 그래프는 상관계수 0.5로 표준화된 변수들을 가지고 시뮬레이션한 예제이다. 첫 번째 패널은 관측치들에 가장 가까운 주성분선(principal component line)을 보여준다. 즉, 이 선은 선과 각 관측치 간 제곱합된 거리가 가장 최소화된 선이다. 이 예제에서 이 선은 $y = x$라고 할 수 있다.

두 번째 패널은 회귀선(regression line)을 보여준다. 이는 선과 각 관측치로부터의 수직 거리(vertical distances)의 제곱합이 가장 작은 선을 말하며, 우리가 일반적으로 말하는 최소자승으로 계산한 선이다: $y = \hat a + \hat b x$. 이때, $\hat a, \hat b$는 $\sum^n_{i=1}(y_i-(\hat a + \hat b x_i))^2$을 최소화하는 값이다. 이 예제에서는 $\hat a = 0$, $\hat b = 0.5$가 된다. 따라서 회귀선의 기울기도 0.5이다.

두 패널 모두 정의 관계를 보여주지만 두 번째 패널 쪽이 $x$로부터 $y$를 예측하고자 할 때, 주어진 $x$의 값에 따른 $y$의 평균 값을 추정함으로써 더 나은 함의를 제공한다. 왜냐하면 주성분선 같은 경우에는 낮은 $x$값에 대한 $y$를 과소예측할 수 있기 때문이다.

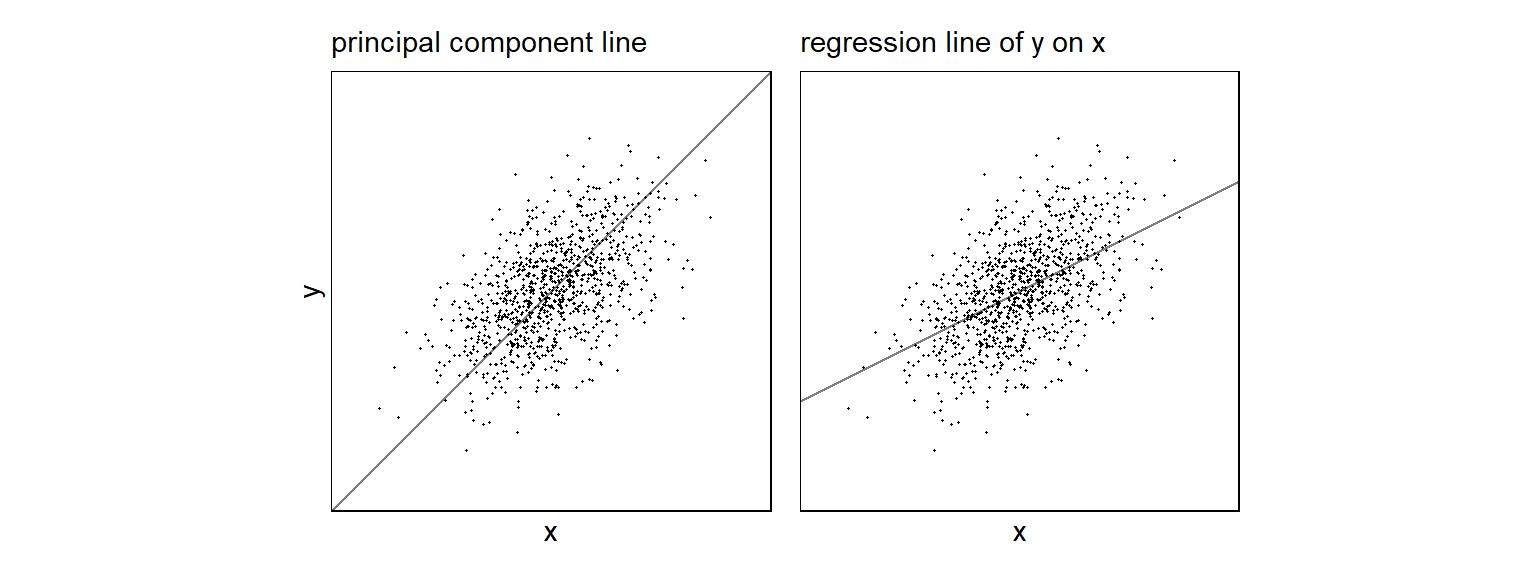
Data simulated from a bivariate normal distribution with correlation 0.5. (a) The principal component line goes closest through the cloud of points. (b) The regression line, which represents the best prediction of y given x, has half the slope of the principal component line.

Figure 12.1: Data simulated from a bivariate normal distribution with correlation 0.5. (a) The principal component line goes closest through the cloud of points. (b) The regression line, which represents the best prediction of y given x, has half the slope of the principal component line.

12.3.2 Regression to the mean

$x$와 $y$가 표준화되어 있을 때, 회귀선은 항상 1보다 작은 기울기를 가지게 된다. 따라서 $x$가 평균보다 1 표준편차 위에 있다면, $y$의 예측값은 0과 평균보다 1 표준편차 위의 값 그 사이 어딘가에 위치하게 된다. 이처럼 선형모델에서 $x$보다 $y$가 평균에 가깝게 예측되는 양상은 “평균으로의 회귀(regression to the mean)”라고도 불린다. Gelman, Hill, and Vehtari (2020, 188–89)는 엄마의 키로 딸의 키를 예측하는 예제를 통해 평균으로의 회귀를 보여준다.

d <-
  d %>% 
  mutate(mom_height      = x,
         daughter_height = y)
head(d)

##              x          y   mom_height daughter_height
## 1 -1.021916981  1.1402296 -1.021916981       1.1402296
## 2 -1.162259081 -1.1362805 -1.162259081      -1.1362805
## 3 -2.000049495 -0.7800456 -2.000049495      -0.7800456
## 4 -0.467207885 -0.6884662 -0.467207885      -0.6884662
## 5  0.007942166  0.3858757  0.007942166       0.3858757
## 6 -1.086100811 -1.4510830 -1.086100811      -1.4510830

다음과 같은 모델을 적합해보자: $\text{daughter_height}_i = \beta_0 + \beta_1 \text{mom_height}_i + \text{error}_i$. 두 변수 모두 표준화된 변수이다.

## stan_glm
##  family:       gaussian [identity]
##  formula:      daughter_height ~ mom_height
##  observations: 1000
##  predictors:   2
## ------
##             Median MAD_SD
## (Intercept) 0.0    0.0   
## mom_height  0.5    0.0   
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 0.8    0.0   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

0.5란 결과는 시간이 지날수록 딸들의 키는 평균 키에 수렴하게 되는(1보다 작으니까 점점 줄어드는 것) 것을 확인할 수 있다.

12.4 Logarithmic transformations

결과변수가 모두 양수일 때, 로그값을 취하는 것이 일반적이다. 왜냐면 음수에 로그값을 취하면 값을 얻을 수 없으니까. 만약 변수에 로그값을 취하고 모델을 분석하고 로그 척도로 예측값을 산출한다면, 그 결과를 다시 지수화(exponentiating)하여 예측값이 $\exp(a) > 0$인 모든 값 $a$에 대하여 반드시 양수가 되도록 결과를 제시해야 한다.

다음과 같은 선형회귀모델이 있다고 하자.

\[\log y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \cdots + \epsilon_i\]

이 모델의 양 변을 지수화하면 다음과 같다.

\[y_i = e^{\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \cdots + \epsilon_i}\]

즉, $B_0 = e^{b_0}, B_1 = e^{b_1}, B_2 = e^{b_2}$는 모두 지수화된 회귀계수 값으로 양수이며, $E_i = e^{\epsilon_i}$는 지수화된 오차항이다(마찬가지로 양수). 원변수 $y_i$의 척도에서 $X_{i1}, X_{i2}$는 곱셉으로 이루어져 있다.

12.4.1 Earnings and height example

키로 소득을 예측하는 모델을 통해서 로그값을 취한 회귀모델을 살펴보자.

12.4.1.1 Direct interpretation of small coefficients on the log scale

소득에 로그값을 취해 모델을 돌려보자.

logmodel_1 <- stan_glm(log(earn) ~ height, 
                       data=earnings %>% dplyr::filter(earn>0),
                       refresh = 0)
print(logmodel_1)

## stan_glm
##  family:       gaussian [identity]
##  formula:      log(earn) ~ height
##  observations: 1629
##  predictors:   2
## ------
##             Median MAD_SD
## (Intercept) 5.9    0.4   
## height      0.1    0.0   
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 0.9    0.0   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

아래의 그래프는 실제 데이터와 적합된 회귀선을 로그 척도와 선형 척도 각각으로 나타내 보여준 것이다.

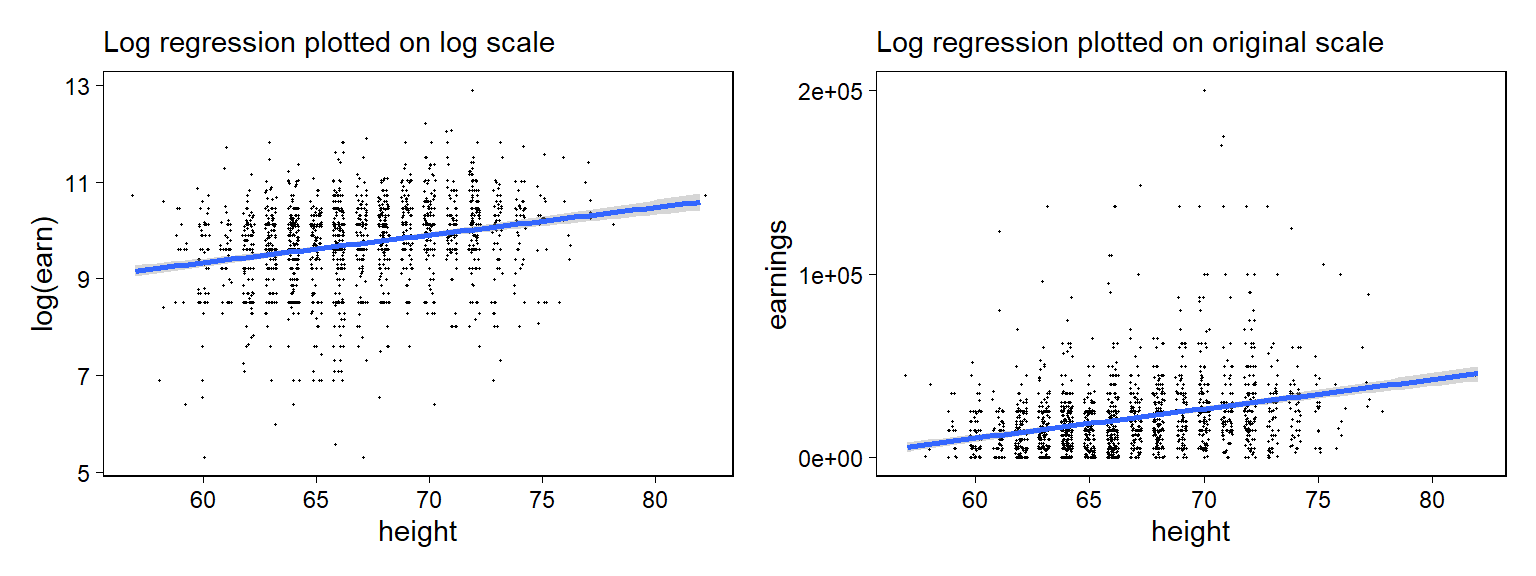
$Regression of earnings on log(height), with curves showing uncertainty the model, $\log(earnings) = a + b <U+2217> height$, fit to data with positive earnings. The data and fit are plotted on the logarithmic and original scales. Compare to the linear model, shown in Figure 12.1a. To improve resolution, a data point at earnings of \$400 000 has been excluded from the original-scale graph.$

Figure 12.2: Regression of earnings on log(height), with curves showing uncertainty the model, $\log(earnings) = a + b <U+2217> height$, fit to data with positive earnings. The data and fit are plotted on the logarithmic and original scales. Compare to the linear model, shown in Figure 12.1a. To improve resolution, a data point at earnings of $400 000 has been excluded from the original-scale graph.

한편 계수값 크기가 증가함에 따라서 로그값을 풀었을 때 나타나는 변화를 시각화해보았다. (-1, 1)로 범위를 한정한 이유는 로그 척도에서 회귀계수는 대개 1보다 작기 때문이다. 로그 척도에서 회귀계수의 1은 예측변수의 한 단위 변화가 결과변수의 $\exp(1)$ 변화로 이어진다는 것을 의미한다.

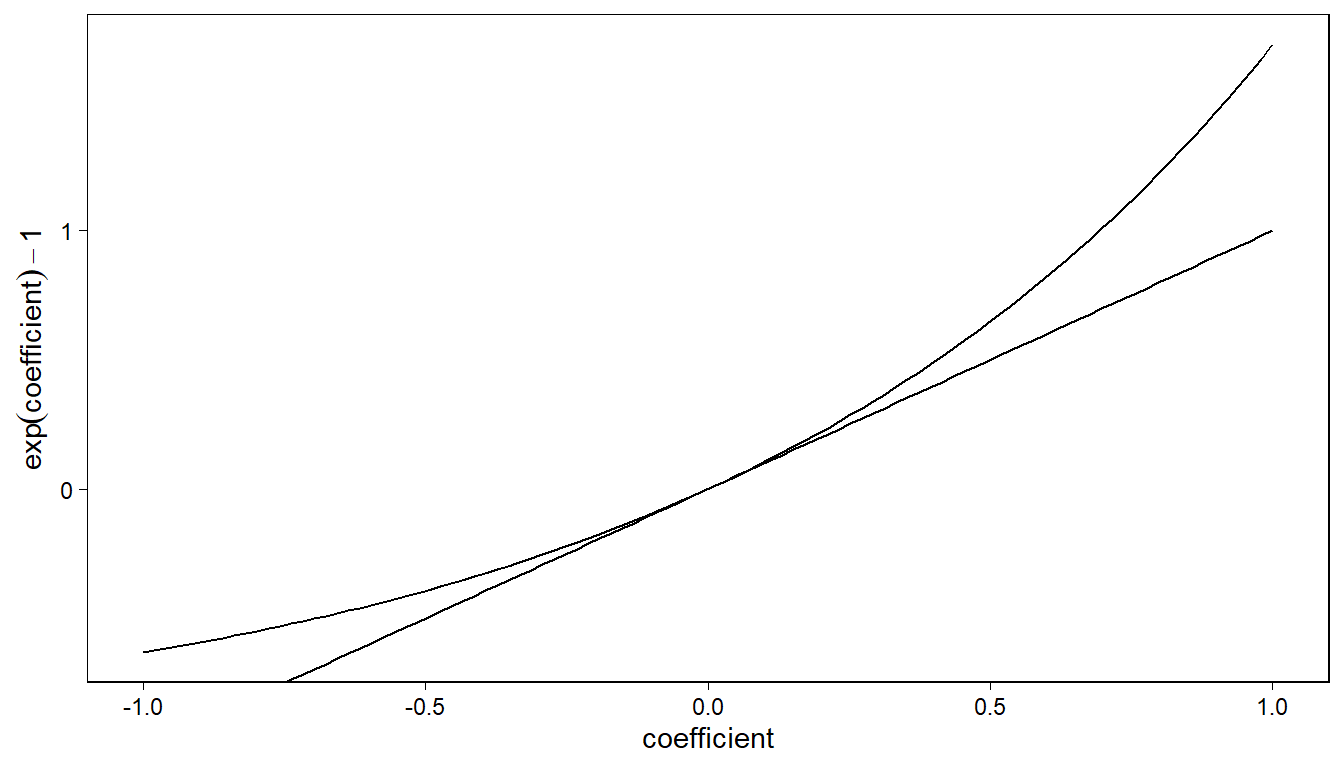
$Interpretation of exponentiated coefficients in a logarithmic regression model as relative difference (curved upper line), and the approximation $\exp(x) = 1 + x$, which is valid for small coefficients $x$ (straight line).$

Figure 12.3: Interpretation of exponentiated coefficients in a logarithmic regression model as relative difference (curved upper line), and the approximation $\exp(x) = 1 + x$, which is valid for small coefficients $x$ (straight line).

12.4.1.2 Predictive checking

적합된 모델로부터 재현된 데이터셋을 시뮬레이션한 뒤 재 적합해 관측된 데이터와 비교해보도록 하자. 먼저 새로운 데이터를 시뮬레이션 한다.

각각 예측변수에 로그값을 취한 경우와 취하지 않고 원변수로 분석한 결과에 대해 시뮬레이션을 한 다음 그 계수값의 표집분포를 밀도 그래프로 보여주는 것이다.

Gelman, Hill, and Vehtari (2020, 191) 는 어떤 식으로든 모델에 변형을 가했을 시, 우리는 적합도의 다른 측면을 평가하기 위해 예측 확인을 수행할 필요가 있다고 제안하고 있다.

물론 베이지안식 접근법이라 시뮬레이션 안 할거면 안 해도 된다.

12.4.2 Why we use natural log rather than log base 10

밑수가 10이나 2인 로그가 아니라 자연로그($e$를 밑수로 하는)를 취하는 이유는 자연로그값을 취한 계수값이 보다 직접적으로 비율 차이로 근사할 수 있는 해석이 가능하기 때문이다. 예를 들어서 자연로그를 취했을 때, 0.05의 계수값은 $x$의 한 단위 변화가 $y$의 약 5% 차이로 이어진다고 해석할 수 있다.

$\log_{10}$과 $\log$ 간의 관계는 다음과 같이 나타낼 수 있다: $\log_{10}(x) = \log(x)/\log(10) = \log(x)/2.3$.

$\log_{10}$을 취할 경우의 장점은 예측값 자체가 해석이 쉬워진다는 것에 있다. 예를 들어, 소득을 회귀분석한 이전의 예제를 생각해볼 때, $\log_{10}10000 = 4$, $\log_{10}(100000)=5$로 값들을 대략적으로 환산하기가 용이하다. 반면에 단점은 계수값을 직접적으로 해석하기가 어렵다는 것이다.

12.4.3 Building a regression model on the log scale

12.4.3.1 Adding another predictor

키 1인치 차이가 소득의 약 6% 차이와 관련이 있다는 것을 얼핏 보기에는 큰 차이같지만 남성이 대개 여성보다 키가 크기 때문에 남성이 더 많은 소득을 가질 수 있다는 것을 고려해야한다. 즉, 6%의 예측차이는 성별의 차이 때문일 수도 있다는 것이다. 성별이 같은 경우에서도 키가 더 큰 사람이 평균적으로 키가 더 작은 사람보다 더 높은 소득을 가질까?

logmodel_2 <- stan_glm(log(earn) ~ height + male, 
                       data = earnings %>% dplyr::filter(earn > 0),
                       refresh = 0)
print(logmodel_2)

## stan_glm
##  family:       gaussian [identity]
##  formula:      log(earn) ~ height + male
##  observations: 1629
##  predictors:   3
## ------
##             Median MAD_SD
## (Intercept) 8.0    0.5   
## height      0.0    0.0   
## male        0.4    0.1   
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 0.9    0.0   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

성별을 통제하자, 키의 1인치 차이는 약 2%의 추정된 예측차이를 보여준다: 이 모델에서 성별이 같은 두 사람은 키 1인치 차이에 따라 평균적으로 소득에 있어서 2%의 차이를 가지는 것이다. 하지만 성별에 대한 예측비교는 더 큰 결과를 보여준다. 남성과 여성이 동일한 키를 가지고 있을 때, 남성의 소득은 $exp(0.37)=1.45$로 남성이 여성보다 약 45% 정도 더 높은 소득을 가지는 것으로 나타난다.

12.4.3.2 Naming inputs

더미변수를 집어넣을 때, 각 카테고리에 대해 1과 0의 값을 갖는 이항변수로 데이터셋에 넣을 수도 있고, 혹은 두 카테고리를 각각 레이블을 갖는 카테고리 변수로 만들 수 있다.

Gelman, Hill, and Vehtari (2020, 192) 의 팁은 이항변수로 코딩해서 데이터셋에 집어넣는 것이 편하고, 이때 1의 값에 대응하는 카테고리를 변수명으로 설정하라는 것이다. 예를 들어, 성별 변수의 경우 male이라고 이름짓고, 남성일 경우에 1의 값을 부여하는 것.

12.4.3.3 Residual standard deviation and $R^2$

회귀모델은 잔차의 표준편차 $\sigma = 0.87$을 갖는데, 이는 약 68%의 로그값을 취한 소득이 예측값의 0.87 내에 위치한다는 것을 보여준다. 한편, $R^2 = 0.08$은 이 모델이 로그 변환을 취한 결과변수의 분산의 약 8%만을 설명해준다는 것을 의미한다.

12.4.3.4 Including an interaction

키와 성별 간의 상호작용을 포함한 모델을 고려해보자. 이때 키에 대한 예측비교는 남성과 여성에 따라 달라질 수 있다.

logmodel_3 <- stan_glm(log(earn) ~ height + male + height:male,
                       data=earnings %>% dplyr::filter(earn>0),
                       refresh = 0)
print(logmodel_3)

## stan_glm
##  family:       gaussian [identity]
##  formula:      log(earn) ~ height + male + height:male
##  observations: 1629
##  predictors:   4
## ------
##             Median MAD_SD
## (Intercept)  8.5    0.7  
## height       0.0    0.0  
## male        -0.8    1.0  
## height:male  0.0    0.0  
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 0.9    0.0   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

이 모델은 다음과 같이 나타낼 수 있다:

\[ \log(\text{earnings}) = 8.48 + 0.02\times \text{height} - 0.76\times \text{male} + 0.02\times \text{height} \times \text{male}. \]

모델의 각 계수값들을 해석해보자.

절편(intercept): height와 male 모두가 0일 때의 로그값을 취한 소득의 예측값. 키가 0일 경우가 없기 때문에 절편의 직접적인 해석에는 의미가 없다.
height의 계수값
- male이 0일 때, 키의 1인치 차이가 로그값을 취한 소득의 예측값 차이와 가지는 관계를 보여준다.
- 키 1인치에 따른 추정된 예측 차이는 여성에 대해 약 2%, 그 추정량의 불확실성은 표준오차 0.01로 나타난다.
male의 계수값
- height가 0일 때, 남성과 여성 간의 로그값을 취한 소득의 예측된 차이를 보여준다. 키가 0일 경우가 없기 때문에 male의 계수값을 직접적으로 해석하지는 않는다.
height:male의 계수값
- 남성과 여성을 비교해서 키가 로그값을 취한 소득을 예측하는 데 나타나는 기울기의 차이를 보여준다.
- 여성에 비해 남성의 로그값을 취한 소득 차이는 키가 1인치 증가할 때 2% 증가하는 것으로 나타나며, 남성들 사이에서는 키 1인치의 차이는 추정된 로그값을 취한 소득의 예측값에 대해 $2\% + 2\% = 4\%$라고 할 수 있다.

12.4.3.5 Linear transformation to make coefficients more interpretable

상호작용 모델에서 예측변수 키에 대해 평균 0, 표준편차 1을 갖도록 리스케일링을 함으로써 해석을 더 직관적으로 할 수 있다.

earnings$z_height <- 
  (earnings$height - mean(earnings$height))/sd(earnings$height)

이 데이터에서 키의 평균과 표준편차는 각각 66.6인치와 3.8인치이다. 표준화한 키 변수를 상호작용모델에 원래의 키를 대체해서 집어넣으면 다음과 같은 결과를 얻을 수 있다.

logmodel_3z <- stan_glm(log(earn) ~ z_height + male + z_height:male,
                       data=earnings %>% dplyr::filter(earn>0),
                       refresh = 0)
print(logmodel_3z)

## stan_glm
##  family:       gaussian [identity]
##  formula:      log(earn) ~ z_height + male + z_height:male
##  observations: 1629
##  predictors:   4
## ------
##               Median MAD_SD
## (Intercept)   9.5    0.0   
## z_height      0.1    0.0   
## male          0.4    0.1   
## z_height:male 0.1    0.1   
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 0.9    0.0   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

이 경우에 표준화된 키 변수는 male이 0일 때, 키의 1 표준편차만큼의 차이가 로그값을 취한 소득의 예측 차이를 보여준다. 상호작용함수의 경우에는 키가 3.8인치 다른 두 남성을 비교할 때, 로그값을 취한 소득에 있어서 $0.06 + 0.08 = 0.14$, 그리고 지수값을 취해서 로그를 풀어내면 $\exp(0.14) = 1.15$, 약 15% 차이를 확인할 수 있다.

12.4.4 Further difficulties in interpretation

모델의 예측변수들이 늘어나면 늘어날수록 비교를 위해서 우리가 고정시켜야 하는 것들이 늘어난다. 또한 변수를 변형할수록 그 해석에도 유의할 필요가 있다.

12.4.5 Log-log model: transforming the input and outcome variables

결과변수뿐 아니라 예측변수에도 로그 변환을 취할 경우에, 계수값은 $x$의 비율적 차이에 따른 $y$의 기대된 비율적 차이로 해석할 수 있다.

earnings$log_height <- log(earnings$height)
logmodel_5 <- stan_glm(log(earn) ~ log_height + male, 
                       data=earnings %>% dplyr::filter(earn>0),
                       refresh = 0)
print(logmodel_5)

## stan_glm
##  family:       gaussian [identity]
##  formula:      log(earn) ~ log_height + male
##  observations: 1629
##  predictors:   3
## ------
##             Median MAD_SD
## (Intercept) 2.8    2.2   
## log_height  1.6    0.5   
## male        0.4    0.1   
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 0.9    0.0   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

키의 1% 차이가 소득에 있어서 1.62%의 예측 차이로 나타난다. male은 카테고리칼 변수이므로 로그값을 취하는 것이 적절치 않다.

12.4.6 Taking logarithms even when not necessary

변수의 분포가 매우 치우쳐 있거나 극단적인 값을 가지고 있을 때, 로그값을 취하고는 한다. 로그값을 취하던 취하지 않던 회귀모델의 적합도에는 큰 차이를 보이지 않는다. 로그값을 취하거나 혹은 스케일링을 하는 이유는 해석가능성을 높이기 위해서이므로, 본인의 모델이 무엇을 분석하고자 하는지 명확하게 인지하고 그 계수값을 좀 더 상식선 상에서 직관적으로 이해할 수 있도록 변환하는 노력이 필요하다.

12.5 Other transformations

12.5.1 Square root transformations

제곱근 변형은 극단적으로 큰 값의 영향력을 제약하고자 할 때 용이하다. 로그값을 취하는 것과 비슷한데, 로그값보다도 더 극단적인 값들의 효과를 억제한다고 볼 수 있을 것이다. 하지만 원변수 모델이나 로그변환 모델에서 확인할 수 있는 명확한 해석이 불가능하다는 단점이 있다.

12.5.2 Idiosyncratic transformations

때로 특정한 문제에 맞춘 변형 방식을 발전시키는 것도 유용하다.

12.5.3 Using continuous rather than discrete predictors

이항 또는 이산형으로 나타나는 많은 변수들이 연속형처럼 유용하게 간주될 수 있다. 하지만 Gelman, Hill, and Vehtari (2020, 196) 은 연속형 변수를 이산형으로 바꾸는 것을 추천하지 않는다. 연속형 변수를 이산형으로 바꾸었을 때 생기는 문제는 정보량의 유실과 더불어 세부적인 경향성을 놓칠 수 있다는 데 있다.

12.5.4 Using discrete rather than continuous predictors

하지만 단순한 모수적 관계가 적절치 않아 보일 때는 어떤 경우에는 연속형 변수를 이산형 변수로 만들어 사용하는 것이 편할 수 있다. 예를 들어, 연령을 원변수 그대로 쓰는 것이 아니라 특정 구간으로 나누어 10대, 20대, 30대 등으로 만드는 것이다.

12.5.5 Index and indicator variables

하나의 변수 안에 이항값을 포함한 더미변수(Gelman, Hill, and Vehtari (2020, 196)에서는 index variables라고 하는)는 모집단을 일단의 카테고리로 나눈다:

male = 1: 남성이 1, 여성은 0으로 코딩
age = 1: 18-29세는 1, 30-44세는 2, 45-64세는 3, 65세 이상은 4로 코딩
state = 1: 알라바마는 1, … , 50은 와이오밍으로 코딩
county = 1: 미국의 3082개 카운티를 코딩.

카테고리에 따라 여러 개로 쪼갠 더미변수(Gelman, Hill, and Vehtari (2020, 196)에서는 indicator variables라고 하는)는 앞의 더미변수에 기초해서 0/1로 예측변수들을 나눈다.

sex_1 = 1: 여성은 1, 그 이외의 경우는 모두 0으로 코딩
sex_2 = 1: 남성은 1, 그 이외의 모든 경우는 모두 0으로 코딩
age_1 = 1: 18-29세이면 1, 아니면 모두 0으로 코딩
age_2 = 1: 30-44세이면 1, 아니면 모두 0으로 코딩
age_3 = 1: 45-64세이면 1, 아니면 모두 0으로 코딩
age_4 = 1: 65세 이상이면 1, 아니면 0으로 코딩
state에 대한 50개 지표
county에 대한 3082개 지표

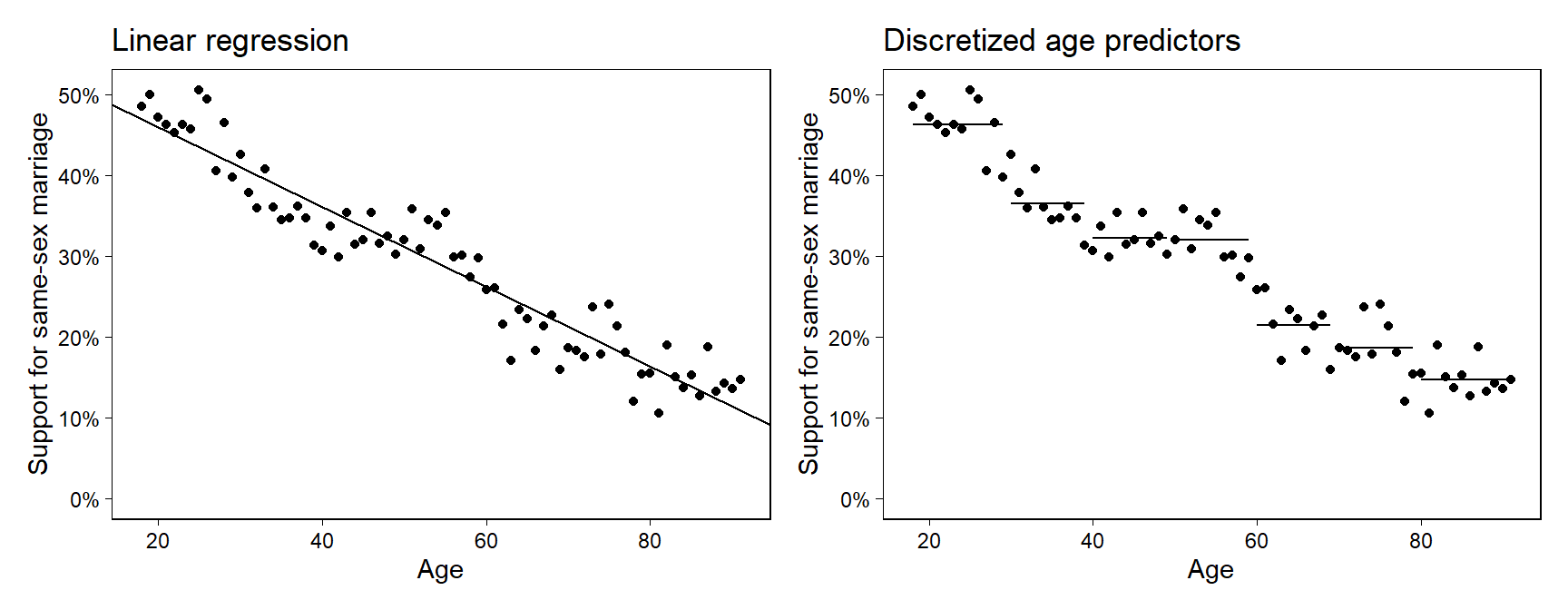
Support for same-sex marriage as a function of age, from a national survey taken in 2004. Fits are shown from two linear regression: (a) using age as a predictor, (b) using indicators for age, discretized into categories.

Figure 12.4: Support for same-sex marriage as a function of age, from a national survey taken in 2004. Fits are shown from two linear regression: (a) using age as a predictor, (b) using indicators for age, discretized into categories.

12.5.6 Indicator variables, identifiability, and the baseline condition

더미변수는 기준이 되는 카테고리를 제외한 나머지 변수들을 모델에 포함한다.

만약 $J$개의 요인이 있다고 한다면, 우리는 $J$개의 더미변수를 만들 수 있다.
그리고 모델에는 절편을 보여주는 상수항과 $J-1$개의 더미변수를 포함한다.

12.6 Building and comparing regression models for prediction

데이터 분석을 수행하기 전에 이론적 모델을 가지고 있다면 더할나위 없겠지만, 대개 실제 데이터 분석은 간단한 모델에서 복잡한 모델로 발전시켜 나아가는 과정을 거친다.

모델들은 데이터 수집 방식 또는 어떤 추론을 하고자 하는지에 따라 달라질 수 있다. 어떤 예측변수들을 모델에 포함할 것인지, 어떻게 변수들을 변형할 것인지 등은 중요한 선택이다. 이 섹션에서는 예측을 위한 모델 수립에 있어서 나타날 수 있는 문제들에 초점을 맞춘다.

12.6.1 General principles

예측을 위한 회귀모델 구축의 일반적인 원칙들은 다음과 같다:

실질적으로 필요한 모든 예측변수들을 모델에 포함하는 것은 결과를 예측하는 데 있어서 중요하다.
이 모든 예측변수들을 반드시 별개의 예측변수로 포함해야만 하는 것은 아니다. 우리는 변수들을 하나로 합쳐 하나의 예측변수로 만들어 모델에 포함할 수도 있다.
큰 효과를 가지는 예측변수에 대해서는 상호작용의 가능성을 고려해볼 수 있다.
모수 추정량에 있어 불확실성을 이해하기 위해서 표준오차를 사용한다. 새로운 데이터가 모델에 추가될 경우에는 그 추정량 또한 변할 수 있다.
예측변수를 추가 또는 제외하는 결정은 일련의 맥락적 이해(사전 지식), 데이터, 그리고 어떤 회귀모델을 사용할 것인지에 기초한다.
1. 만약 예측변수의 계수값이 정확히 추정된다면(작은 표준오차), 일반적으로 모델에 포함시키는 것이 예측을 개선시킨다.
2. 만약 계수의 표준오차가 크고, 그 변수가 모델에 포함되어야 할 실질적 이유를 갖지 못한다면, 그 변수를 모델에서 제외하는 것도 필요하다. 왜냐하면 그 변수가 모델에 포함됨으로써 다른 예측변수들의 추정된 계수값을 불안정하게 하고 예측 오차를 더 높일 수 있기 때문이다.
3. 만약 어떤 예측변수가 문제를 푸는 데 중요하다면, 그 계수값이 작거나 혹은 표준오차가 크고 통계적 유의성을 갖지 못하더라도 모델에 남겨두는 것ㅇ르 권한다.
4. 만약 어떤 계수가 상식적으로 말이 안 되는 결과를 보여준다면, 왜 그런 결과가 나타났는지를 이해하기 위해 노력할 필요가 있다. 만약 표준오차가 크다면, 그 추정량은 무작위 변동량으로 설명될 수도 있다. 만약 표준오차가 작다면, 그 계수를 이해하기 위해 더 노력할 필요가 있다.

위의 전략들이 우리의 문제를 완전히 해결해주는 것은 아니지만 중요한 정보를 버린다던가 하는 실수를 저지르지 않는 데는 도움을 줄 수 있다.

12.6.2 Example: predicting the yields of mesquite bushes

예제를 통해 살펴보자. 실제로 수확하기 전에 측정된 식물과 관련된 자료를 통해 메스키트(mesquite)의 총생산을 추정하려 한다고 하자. 측정은 두 가지로 이루어진다. 첫 번째는 26개 메스키트로 이루어진 집단이며, 다른 하나는 또 다른 20개의 메스키트인데 햇수가 다르게 측정된 집단이다. 모든 데이터는 동일한 지리적 위치(ranch)에서 획득되었지만, 엄밀히 말하면 무작위 표본은 아니다.

결과변수는 실제로 수확하는 데에서 얻은 광합성 물질의 총 무게(in grams)이며, 예측변수는 다음과 같다.

Inputs	Description
diam1:	diameter of the canopy (the leafy area of the bush) in meters, measured along the longer axis of the bush
diam2:	canopy diameter measured along the shorter axis
conopy_height:	height of the canopy
total_height:	total height of the bush
density:	plant unit density (# of primary stems per plant unit)
group:	group of measurements (0 for the first group, 1 for the second)

회귀모델을 이용해서 잎의 무게를 예측해볼만 하다. 여기서는 간단히 weight를 결과변수로 하고 나머지 예측변수들을 모두 포함한 모델을 구축한다.

fit_1 <- stan_glm(formula = weight ~ diam1 + diam2 + canopy_height +
                    total_height + density + group,
                  data=mesquite, refresh = 0)
print(fit_1)

## stan_glm
##  family:       gaussian [identity]
##  formula:      weight ~ diam1 + diam2 + canopy_height + total_height + density + 
##     group
##  observations: 46
##  predictors:   7
## ------
##               Median  MAD_SD 
## (Intercept)   -1093.4   185.3
## diam1           194.1   116.9
## diam2           371.5   127.1
## canopy_height   352.6   205.1
## total_height   -103.7   185.9
## density         131.8    35.5
## groupMCD        365.0   103.3
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 273.4   29.9 
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

이 모델의 결과를 LOO 교차 타당화를 통해서 평가할 수 있다.

(loo_1 <- loo(fit_1))

## 
## Computed from 4000 by 46 log-likelihood matrix
## 
##          Estimate   SE
## elpd_loo   -335.1 13.2
## p_loo        16.8  9.2
## looic       670.1 26.4
## ------
## Monte Carlo SE of elpd_loo is NA.
## 
## Pareto k diagnostic values:
##                          Count Pct.    Min. n_eff
## (-Inf, 0.5]   (good)     42    91.3%   784       
##  (0.5, 0.7]   (ok)        1     2.2%   1959      
##    (0.7, 1]   (bad)       2     4.3%   21        
##    (1, Inf)   (very bad)  1     2.2%   3         
## See help('pareto-k-diagnostic') for details.

진단 통계량은 LOO 컴퓨테이션이 불안정하다는 것을 보여준다. 그렇다면 K-fold 교차 타당화를 사용해볼 수 있다.

(kfold_1 <- kfold(fit_1, K=10))

## 
## Based on 10-fold cross-validation
## 
##            Estimate   SE
## elpd_kfold   -367.1 41.2
## p_kfold          NA   NA
## kfoldic       734.3 82.5

loo 진단 통계량은 정확하게 문제를 보여주며, kfold 추정량은 더 회의적인 결과를 보여준다.

각 예측변수의 중요성을 이해하기 위해서, 각 변수들의 범주에 대해서 알 필요가 있다.

##               vars  n   mean     sd median trimmed    mad   min    max   range
## obs              1 46  23.50  13.42  23.50   23.50  17.05  1.00   46.0   45.00
## group*           2 46   1.57   0.50   2.00    1.58   0.00  1.00    2.0    1.00
## diam1            3 46   2.10   0.88   1.95    2.00   0.82  0.80    5.2    4.40
## diam2            4 46   1.57   0.80   1.52    1.50   0.78  0.40    4.0    3.60
## total_height     5 46   1.48   0.47   1.50    1.47   0.44  0.65    3.0    2.35
## canopy_height    6 46   1.11   0.38   1.10    1.09   0.32  0.50    2.5    2.00
## density          7 46   1.67   1.59   1.00    1.29   0.00  1.00    9.0    8.00
## weight           8 46 559.66 642.83 361.85  454.09 326.84 60.20 4052.0 3991.80
##                skew kurtosis    se
## obs            0.00    -1.28  1.98
## group*        -0.25    -1.98  0.07
## diam1          1.24     1.90  0.13
## diam2          0.97     0.95  0.12
## total_height   0.47     0.65  0.07
## canopy_height  0.93     1.99  0.06
## density        3.11     9.93  0.23
## weight         3.60    16.33 94.78

이번에는 모델의 변수에 로그값을 취해 적합해보도록 하자. 이 경우, 그 효과는 가산적(additive)이라기 보다는 곱셈의 결과(multiplicative)라고 할 수 있다.

fit_2 <- stan_glm(formula = log(weight) ~ log(diam1) + log(diam2) + 
                    log(canopy_height) +
                    log(total_height) + log(density) + 
                    group, data=mesquite,
                  refresh = 0)
print(fit_2)

## stan_glm
##  family:       gaussian [identity]
##  formula:      log(weight) ~ log(diam1) + log(diam2) + log(canopy_height) + 
##     log(total_height) + log(density) + group
##  observations: 46
##  predictors:   7
## ------
##                    Median MAD_SD
## (Intercept)        4.8    0.2   
## log(diam1)         0.4    0.3   
## log(diam2)         1.2    0.2   
## log(canopy_height) 0.4    0.3   
## log(total_height)  0.4    0.3   
## log(density)       0.1    0.1   
## groupMCD           0.6    0.1   
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 0.3    0.0   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

이 결과 우리는 캐노피 높이의 $x$% 차이가 잎 무게의 약 0.4$x$% 만큼의 양의 차이(positive difference)와 관계가 있다고 진술할 수 있다.

예측모델 비교에서 우리는 LOO 교차 타당화를 해볼 수 있다.

(loo_2 <- loo(fit_2))

## 
## Computed from 4000 by 46 log-likelihood matrix
## 
##          Estimate   SE
## elpd_loo    -19.4  5.4
## p_loo         7.6  1.5
## looic        38.9 10.7
## ------
## Monte Carlo SE of elpd_loo is 0.1.
## 
## Pareto k diagnostic values:
##                          Count Pct.    Min. n_eff
## (-Inf, 0.5]   (good)     43    93.5%   601       
##  (0.5, 0.7]   (ok)        3     6.5%   341       
##    (0.7, 1]   (bad)       0     0.0%   <NA>      
##    (1, Inf)   (very bad)  0     0.0%   <NA>      
## 
## All Pareto k estimates are ok (k < 0.7).
## See help('pareto-k-diagnostic') for details.

진단 통계량은 LOO 컴퓨테이션이 안정적이라는 것을 보여준다.

12.6.3 Using the Jacobian to adjust the predictive comparison after a transformation

이 파트는 딱히 다룰 필요는 없을 것 같다. 그냥 서로 다른 변환 방법을 사용해서 모델을 추정하였을 경우, 그 결과의 불확실성을 포착하고 비교 및 분석할 필요가 있다는 정도의 개념만 가지고 가면 될 듯하다.

12.6.4 Constructing a simpler model

단순한 모델에서 얻을 수 있는 더 나은 성과와 이해는 우리가 모든 회귀계수들에 대해 약한 사전 분포를 가지고 적합한다는 것에 있다. 약한 사전 분포를 가지고 데이터에서 추론을 이끌어내며, 표본의 규모가 작거나 예측변수가 서로 매우 상관되어 있는 경우, 계수값은 잘 식별되지 않고 추정량 또한 잡음이 많아진다. 변수를 제외하거나 혹은 결합하는 것은 예측력을 많이 잃지 않으면서도 쉽게 해석할 수 있도록 하는, 안정적인 추정량을 얻기 위한 방법이다. 또 다른 접근법은 모델의 모든 예측변수들을 유지하되 추정량을 안정화시키기 위해 계수값에 대한 강한 사전분포를 가지는 것이다(Gelman, Hill, and Vehtari 2020: 206).

12.7 Models for regression coefficients

빈도주의적 접근법으로 계수와 표준오차에 대한 점추정량으로 신뢰구간만 보여주는 것보다 베이지언을 이용해 시뮬레이션된 실제 데이터로 계수를 둘러싼 불확실성을 일종의 표집분포로 보여주는 것의 장점에 대해 논의하고 있는 파트이다. 베이지언을 사용할게 아니라면 자세히 볼 필요는 없고 이런 것이 있구나 하고 넘어가면 될 듯하다.

12.7.1 Other models for regression coefficients

결국은 이전에 가중치에 대해 논의했던 것처럼, 계수값을 왜곡시키는 요인이 어떤 것인지 식별하고 그것에 대한 가중치/제약을 부여하여 보다 안정적이고 신뢰할 수 있는 계수값을 추정하고자 하는 노력들이 필요하다는 것을 주장하는 파트이다. 여기서는 Lasso 회귀모델과 같은 종류의 회귀모델을 예제로 들고 있다.

References

Gelman, Andrew, Jennifer Hill, and Aki Vehtari. 2020. Regression and Other Stories. Cambridge University Press.