Chapter 13 Logistic regression

선형회귀모델은 가산형 모델(additive model)로 결과변수인 $y$가 0 또는 1의 값을 취하는 이항 결과변수에는 적절하지 않다.

이항변수로 모델을 만들기 위해서는 $y=a+bx$라는 기본 모델에 두 가지를 더 추가해야 한다.
1. 0과 1 사이로 결과를 한정하는 비선형 변환
2. 결과를 확률로 취급하여 무작위 이항 결과로 이끌어내는 모델

모델의 비선형성은 해석과 모델 수립을 더 까다롭게 만드는 부분이 있어서 이 챕터에서는 그와 관련된 내용을 주로 다룬다.

13.1 Logistic regression with a single predictor

로지스틱(logistic) 함수는 다음과 같다:

\[ \text{logit}(x) = \log\bigg(\frac{x}{1-x}\bigg), \]

이 함수를 통해 우리는 $(0, 1)$의 범주를 $(-\infty, \infty)$로 취급하여 확률을 모델링하는 데 유용하게 사용할 수 있다. 역함수를 취하면 단위 범위로 다시 되돌릴 수 있다:

\[ \text{logit}^{-1}(x) = \frac{e^x}{1+e^x}. \]

R에서는 로지스틱 분포를 이용해 이와 같은 로지스틱 함수를 확인할 수 있다.

logit <- qlogis
invlogit <- plogis

이항변수를 모델링하는 데 있어 로지스틱 변환의 용법에 대해 살펴보자.

13.1.1 Example: modeling political preference given income

전통적으로 보수적인 정당들은 고소득 유권자들로부터 더 많은 지지를 받아왔다. 1992년 NES로부터 이 패턴을 분석해보기 위해 전통적인 로지스틱 회귀모델을 사용해보자.

NES 설문조사에서 각 응답자 $i$에 대해, 응답자가 조지 부시를 선호할 경우에는 $y_i=1$, 응답자가 빌 클린턴을 선호할 경우에는 $y_i = 0$으로 코딩하며 다른 후보자에 대한 선호나 의견은 제외하였다.
예측변수는 응답자의 소득 수준으로 5점 척도로 측정되었다.

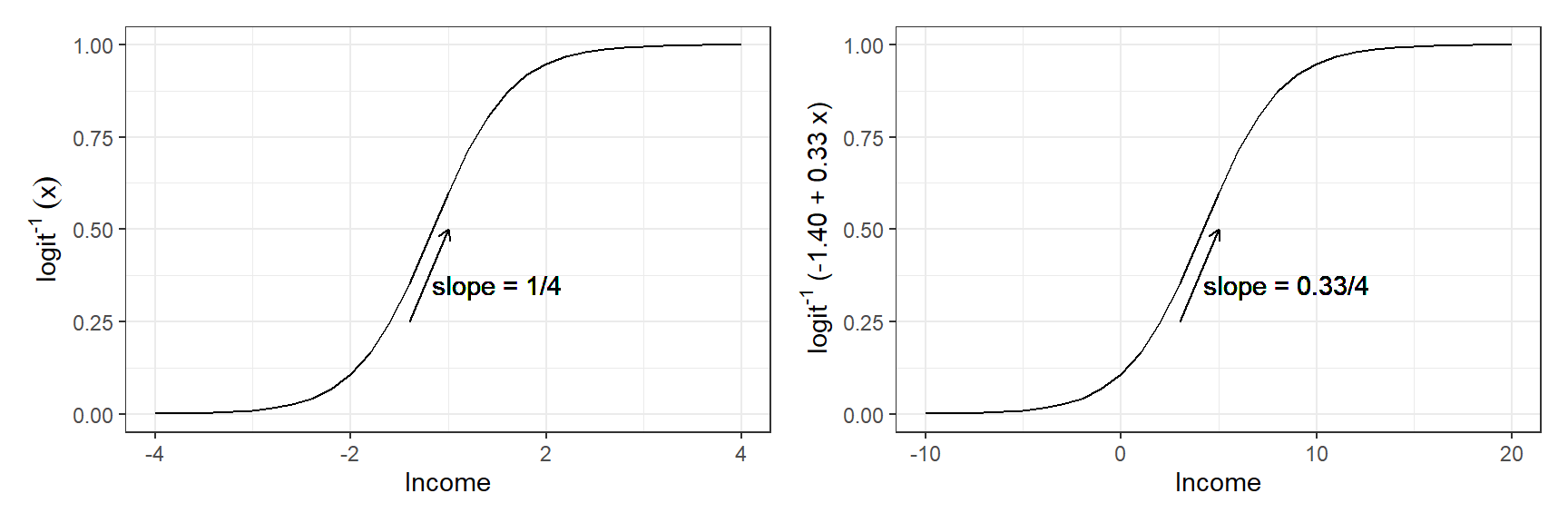
$(a) Inverse logit function $\text{logit}^{-1}(x)$ from (13.1): the transformation from linear predictors to probabilities that is used in logistic regression. (b) An example of the predicted probabilities from a logistic regression model: $y = \text{logit}^{-1}(-1.40 + 0.33x)$. The shape of the curve is the same, but its location and scale have changed; compare the x-axes on the two graphs. On each graph, the vertical dotted line shows where the predicted probability is 0.5: in graph (a), this is at $\text{logit}(0.5) = 0$; in graph (b), the halfway point is where $-1.40 + 0.33x = 0$, which is $x = 1.40/0.33 = 4.2$. As discussed in Section 13.2, the slope of the curve at the halfway point is the logistic regression coefficient divided by 4, thus 1/4 for $y = \text{logit}^{-1}(x)$ and $0.33/4$ for $y = \text{logit}^{-1}(-1.40 + 0.33x)$. The slope of the logistic regression curve is steepest at this halfway point.$

Figure 13.1: (a) Inverse logit function $\text{logit}^{-1}(x)$ from (13.1): the transformation from linear predictors to probabilities that is used in logistic regression. (b) An example of the predicted probabilities from a logistic regression model: $y = \text{logit}^{-1}(-1.40 + 0.33x)$. The shape of the curve is the same, but its location and scale have changed; compare the x-axes on the two graphs. On each graph, the vertical dotted line shows where the predicted probability is 0.5: in graph (a), this is at $\text{logit}(0.5) = 0$; in graph (b), the halfway point is where $-1.40 + 0.33x = 0$, which is $x = 1.40/0.33 = 4.2$. As discussed in Section 13.2, the slope of the curve at the halfway point is the logistic regression coefficient divided by 4, thus 1/4 for $y = \text{logit}^{-1}(x)$ and $0.33/4$ for $y = \text{logit}^{-1}(-1.40 + 0.33x)$. The slope of the logistic regression curve is steepest at this halfway point.

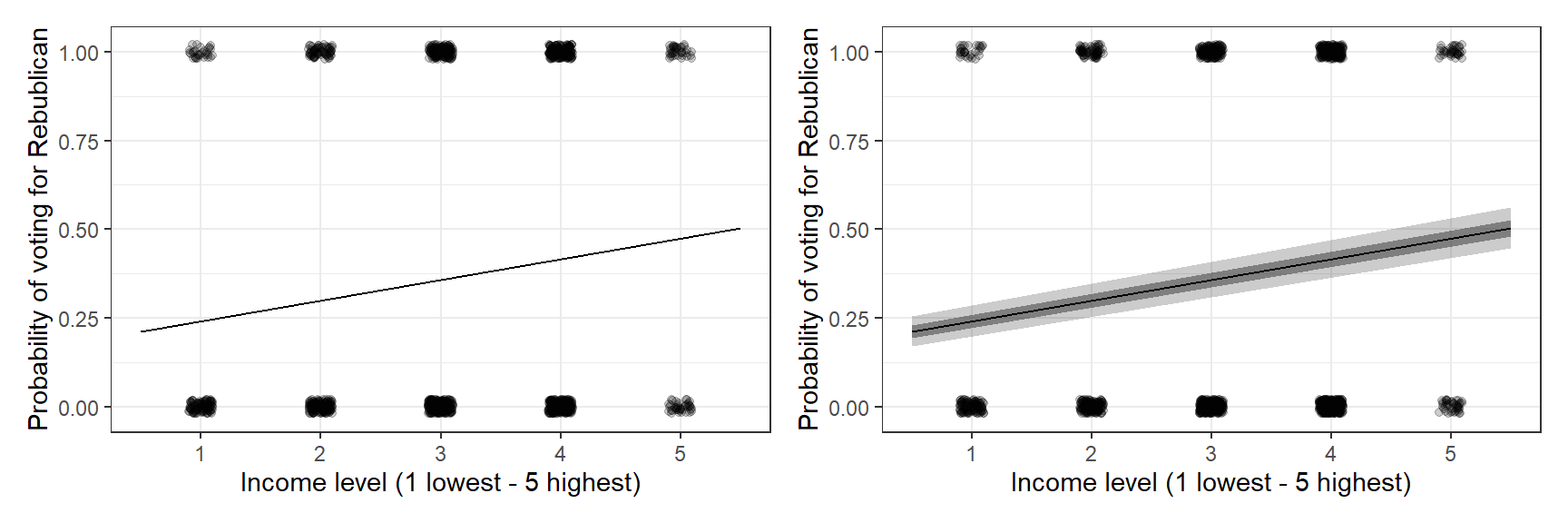
Logistic regression estimating the probability of supporting George Bush in the 1992 presidential election, as a function of discretized income level. Survey data are indicated by jittered dots. In this example, little is revealed by these jittered points, but we want to emphasize here that the data and fitted model can be put on a common scale. (a) Fitted logistic regression: the thick line indicates the curve in the range of the data; the thinner lines at the ends show how the logistic curve approaches 0 and 1 in the limits. (b) In the range of the data, the solid line shows the best-fit logistic regression, and the light lines show uncertainty in the fit.

Figure 13.2: Logistic regression estimating the probability of supporting George Bush in the 1992 presidential election, as a function of discretized income level. Survey data are indicated by jittered dots. In this example, little is revealed by these jittered points, but we want to emphasize here that the data and fitted model can be put on a common scale. (a) Fitted logistic regression: the thick line indicates the curve in the range of the data; the thinner lines at the ends show how the logistic curve approaches 0 and 1 in the limits. (b) In the range of the data, the solid line shows the best-fit logistic regression, and the light lines show uncertainty in the fit.

Figure 13.2는 데이터와 적합된 로지스틱 회귀선을 보여준다. 이 회귀곡선은 0과 1 사이로 그 범위가 제약되어 있다. 우리는 이 회귀선을 주어진 $x$에서의 $y=1$일 확률, $\Pr(y = 1|x)$라고 해석할 수 있다.

13.1.2 The logistic regression model

선형회귀모델, $X\beta + \text{error}$에 0과 1의 값을 갖는 데이터 $y$를 적합할 때, 문제가 있을 수 있다. 이 모델의 계수값은 확률 차이로 해석될 수 있지만, 예측을 위한 모델에 사용하기에는 어려움이 있고, 연속형인 것처럼 이산형 결과변수를 모델링할 경우 정보를 소실하게 될 수도 있다.

대신, 결과변수 $y_i$가 독립적이라는 가정 하에서 우리는 $y=1$일 확률을 다음과 같이 모델링한다:

\[ \Pr(y_i = 1) = \text{logit}^{-1}(X_i\beta) \]

이때, $X\beta$는 선형 예측변수를 의미한다. 위의 수식은 다음과 같이 바꾸어 쓸 수 있다:

\[ \begin{aligned} \Pr(y_i = 1)&= p_i\\ \text{logit}(p_i)&= X_i\beta \end{aligned} \] Gelman, Hill, and Vehtari (2020, 219)는 로짓의 역함수인 $\text{logit}^{-1}$로 분석하는 것을 선호한다고 밝히고 있다. 왜냐하면 이 경우 선형 예측변수들을 확률적 개념으로 해석하는 데 조금 더 자유로워지기 때문이다.

로지스틱의 역함수는 곡선의 형태를 취하기 때문에, 고정된 $x$의 값의 차이에 따른 $y$의 기대값 변화는 일정하지 않다. 즉, $x$가 1에서 2로 변할 때의 $y$의 기대값 결과와 $x$가 2에서 3으로 변할 때의 $y$의 기대값의 차이는 동일하지 않다는 것이다.

$\text{logit}(0.5) = 0$이고 $\text{logit}(0.6) = 0.4$이다. 여기서 0.4의 로짓 척도는 약 확률적으로 50%에서 60%의 변화를 의미한다.
$\text{logit}(0.9) = 2.2$이고 $\text{logit}(0.93) = 2.6$이다. 여기서 0.4의 로짓 척도는 약 확률적으로 90%에서 93%의 변화를 의미한다.

일반적으로 로짓 척도의 특정한 변화는 결과적으로는 확률 척도로 변환가능하며, 0과 1 사이에 놓이게 되지만 그 구간의 변화는 일정하지 않다.

13.1.3 Fitting the model using stan_glm and displaying uncertainty in the fitted model

Gelman, Hill, and Vehtari (2020, 219)는 예측 불확실성을 보여주기 위해서 stan_glm을 이용해서 시뮬레이션을 하지만, 이 리딩노트에서는 기존의 glm으로 추정한 계수 결과를 mvtnorm 패키지의 rmvnorm을 이용해 시뮬레이션하는 접근법을 취하고자 한다. 결과는 stan_glm과 다르지 않다. 계수값의 불확실성을 모수적 시뮬레이션을 이용해 무작위 추출한 표집분포로 보여주는 것이다.

fit_1 <- glm(rvote ~ income, 
           family = binomial(link = "logit"), data = nes_1992)
sims_1 <- MASS::mvrnorm(20, mu = coef(fit_1), Sigma = vcov(fit_1))
n_sims <- nrow(sims_1)
for (j in sample(n_sims, 20)){
curve(invlogit(sims_1[j,1] + sims_1[j,2]*x), col="gray", lwd=0.5, add=TRUE)
}

## Error in plot.xy(xy.coords(x, y), type = type, ...): plot.new has not been called yet

13.2 Interpreting logistic regression coefficients and the divide-by-4 rule

로지스틱 회귀모델의 계수는 비선형성으로 인해 해석이 까다로울 수 있다. 따라서 계수를 이해하기 편하도록 일반화하는 과정이 필요하다.

13.2.1 Evaluation at and near the mean of the data

로지스틱 함수의 비선형성은 확률 척도로 해석하고자 할 때, 어느 지점의 변화를 살펴볼 것인지를 결정해야 한다. 기본적으로는 예측변수들의 평균을 이용하는 것이 유용하다.

선형회귀모델처럼, 절편은 다른 모든 예측변수들이 0일 경우를 가정한 값으로 해석할 수 있다.
예를 들어, 아래의 코드는 응답자의 소득 수준이 평균이며, 다른 모든 예측변수들이 0일 경우에 부시를 지지할 확률을 보여준다고 할 수 있다.

invlogit(coef(fit_1)[1] + coef(fit_1)[2]*mean(nes_1992$income))

## (Intercept) 
##   0.3433863

invlogit = plogis (Gelman, Hill, and Vehtari 2020: 217).
평균 소득 수준($\bar x$)이 3.1이라고 할 때, 이 3.1에서 한 단위 증가에 따른 확률을 변화를 살펴볼 수 있다.
- $x = 3$일 때와 $x = 2$일 때, $\Pr(y = 1)$일 확률의 변화를 살펴보는 것
- $\text{logit}^{-1}(-14.0+0.33\times 3)-\text{logit}^{-1}(-14.0+0.33\times 2) = 0.08$.

13.2.2 The divide-by-4 rule

로지스틱 곡선은 $\alpha + \beta x = 0$이기 때문에 $\text{logit}^{-1}(\alpha + \beta x) = 0.5$인 중앙을 기점으로 그 기울기가 가팔라진다. 곡선의 기울기, 로지스틱 함수에 도함수를 취한 값은 그 중앙에서 최대값을 갖는다: $\beta e ^0/(1+e^0)62 = \beta/4$. 따라서 $\beta/4$는 $x$의 단위 차이에 따른 $\Pr(y = 1)$의 차이가 가장 큰 값이라고 할 수 있다.

따라서, 우리는 로지스틱 회귀계수(상수항을 제외한)의 값을 4로 나누어줌으로써, $x$의 한 단위 차이에 따른 예측 차이의 상한 경계값(upper bound)을 구할 수 있다. 상한 경계값은 로지스틱 곡선의 대략 중간에 위치한 값을 보여주며, 확률적으로는 0.5에 해당하는 지점이라고 할 수 있다.

13.2.3 Interpretation of coefficients as odds ratios

로지스틱 회귀계수를 해석하는 또 다른 방법으로는 오즈비(odds ratio)를 통한 접근법이 있다. 만약 결과가 두 가지 확률을 갖는다면($p, 1-p$), $\frac{p}{1-p}$를 우리는 승산, 오즈(odds)라고 한다. 오즈가 1이라는 얘기는 확률이 0.5라는 것, 결과가 동등하게 양분되어 나타났다는 것을 의미한다. 오즈가 0.5나 2.0일 경우는 $\frac{1}{3}, \frac{2}{3}$을 의미한다. 이 두 오즈 간의 비율을 구하면, $\frac{p_1}{1-p_1}/\frac{p_2}{1-p_2}$ 우리는 오즈비를 얻게 된다. 즉, 오즈비가 2라는 것은 $p=0.33$에서 $p=0.5$의 변화, 혹은 $p=0.5$에서 $0.67$로의 변화를 보여주는 것이라고 할 수 있다.

확률 대신에 오즈비로 분석할 경우의 이점은, 0와 1로 제약하지 않고 오즈비 척도로 계수를 비교할 수 있다는 것에 있다.
로지스틱 회귀계수의 로그값을 풀어내면 오즈비로 해석할 수 있다. 하나의 변수를 가진 모델을 대상으로 할 때, 다음과 같은 공식이 성립한다:

\[ \log\Bigg(\frac{\Pr(y= 1|x)}{\Pr(y = 0|x)} \Bigg) = \alpha + \beta x. \]

$x$를 한 단위 추가할 경우, 우리는 $\beta$만큼이 양 변에 추가되는 결과를 확인할 수 있다.
- 만약 양 변에 로그를 푼다면, 오즈 값에 $e^\beta$를 곱하ㄴ결과가 된다.

13.2.4 Coefficient estimates and standard errors

전통적인 로지스틱 회귀분석의 계수는 최대가능도를 사용해 주청되며, 그 표준오차는 추정량의 불확실성을 나타낸다.

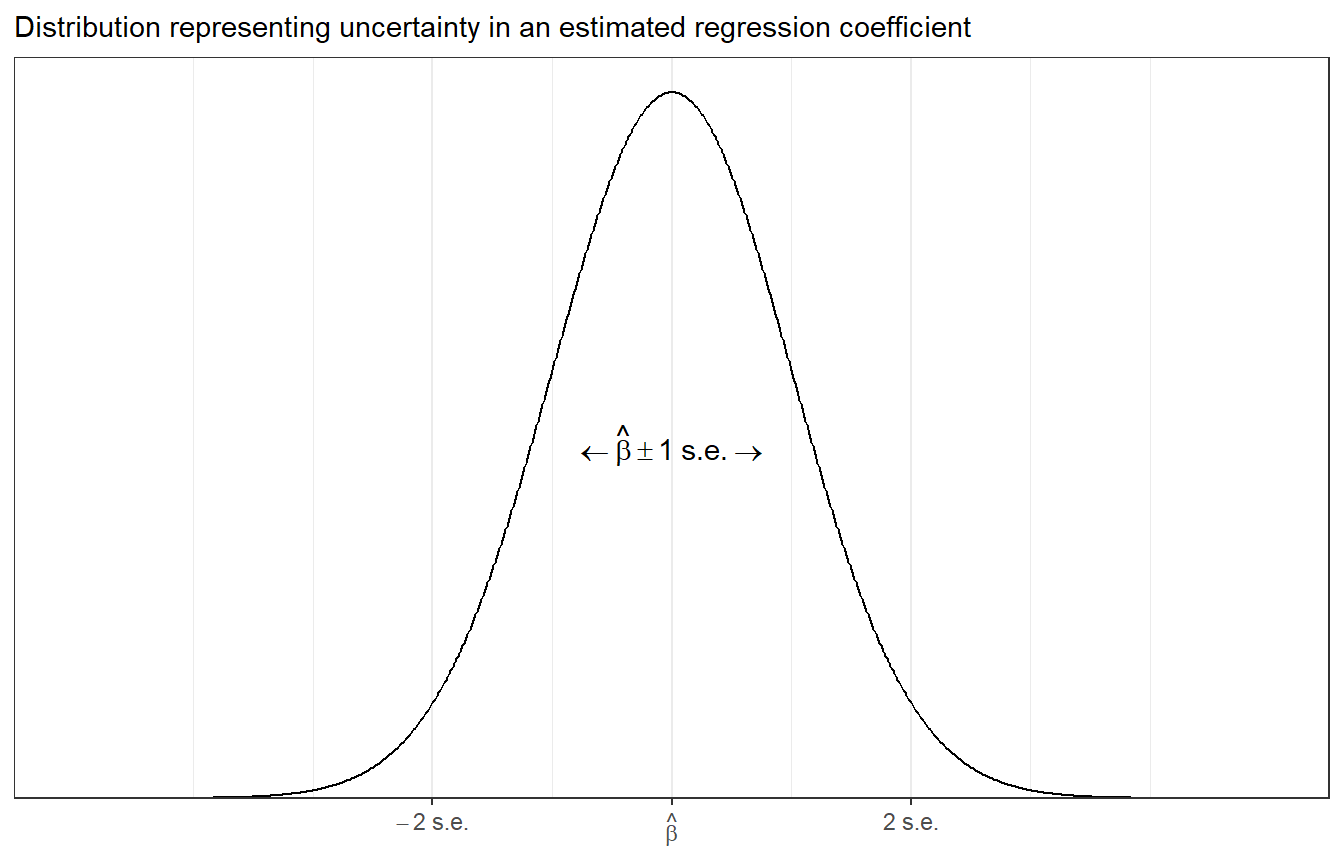
$Distribution representing uncertainty in an estimated regression coefficient (repeated from Figure 4.1). The range of this distribution corresponds to the possible values of $\beta$ that are consistent with the data. When using this as an uncertainty distribution, we assign an approximate 68% chance that $\beta$ will lie within 1 standard error of the point estimate, $\hat \beta$, and an approximate 95% chance that β will lie within 2 standard errors. Assuming the regression model is correct, it should happen only about 5% of the time that the estimate, $\hat \beta$, falls more than 2 standard errors away from the true $\beta$.$

Figure 13.3: Distribution representing uncertainty in an estimated regression coefficient (repeated from Figure 4.1). The range of this distribution corresponds to the possible values of $\beta$ that are consistent with the data. When using this as an uncertainty distribution, we assign an approximate 68% chance that $\beta$ will lie within 1 standard error of the point estimate, $\hat \beta$, and an approximate 95% chance that β will lie within 2 standard errors. Assuming the regression model is correct, it should happen only about 5% of the time that the estimate, $\hat \beta$, falls more than 2 standard errors away from the true $\beta$.

13.2.5 Statistical significance

선형회귀모델과 마찬가지로 추정량은 통상 0으로부터 최소 2 표준오차만큼 떨어져 있을 경우에는 95% 신뢰구간이 0을 포함하지 않기 때문에 통계적으로 유의미하다고 칭해진다.

하지만 Gelman, Hill, and Vehtari (2020, 222)는 통계적 유의성이라는 것에 집착하지 않을 것을 권한다.
추정량이 통계적으로 유의하지 않더라도 여전히 모집단 수준에서는 어떠한 효과 혹은 관계를 가지고 있을 수 있기 때문이다.

13.2.6 Displaying the results of several logistic regressions

아래의 그래프는 1952년부터 2000년까지의 사전 설문조사로 집계한 대통령 후보자 선호에 대한 소득의 계수 추정량에 대한 $\pm$ 1 표준오차를 보여준다. 소득 수준이 높은 응답자일수록 공화당 후보를 지지할 가능성을 일관되게 높은 것을 확인할 수 있다. 그러나 그 관계는 시간이 흐를 수록 더욱 강해지는 것 또한 확인할 수 있다.

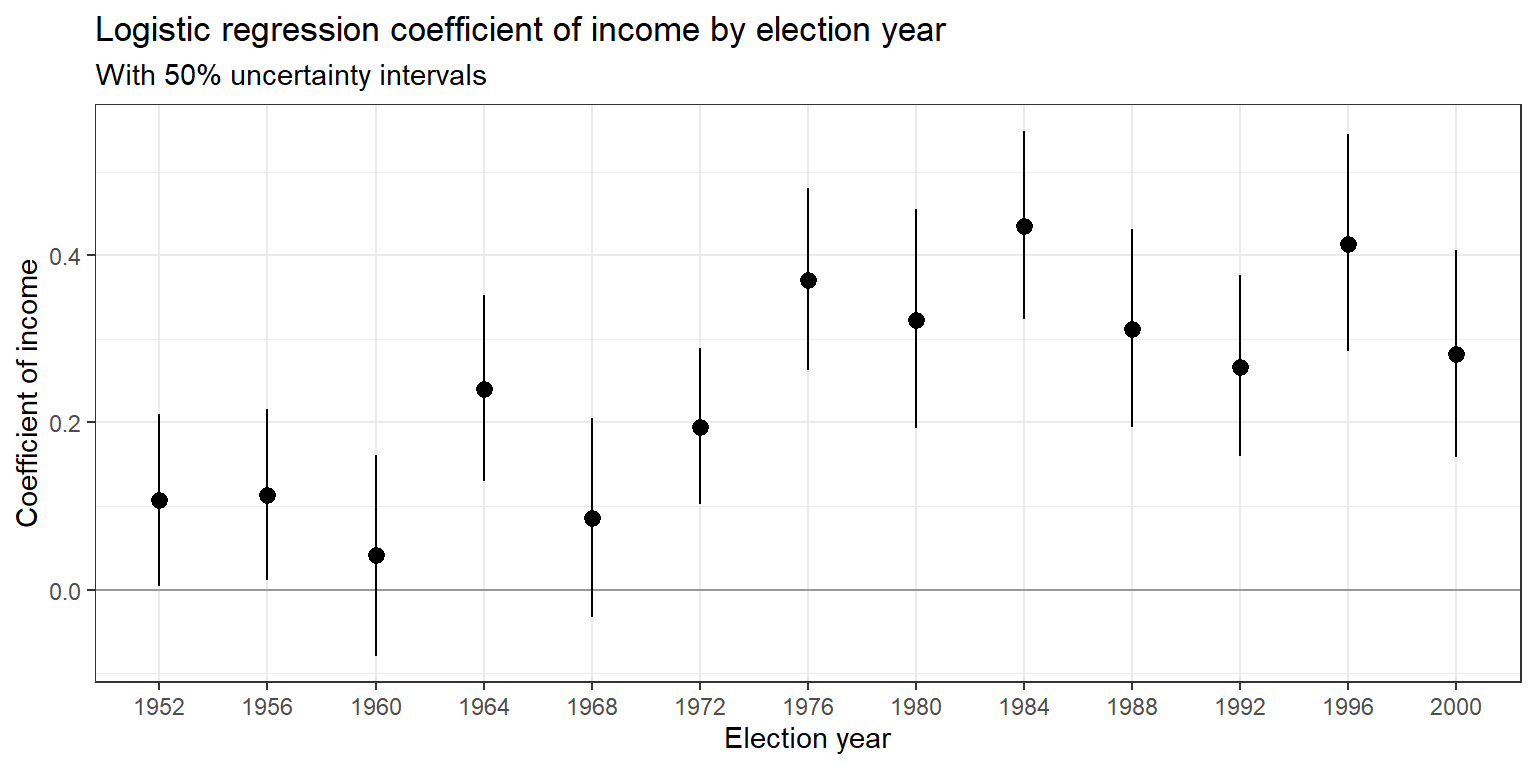
$Coefficient of income (on a 1<U+2013>5 scale) with $\pm 1$ standard-error bounds in logistic regressions predicting Republican preference for president, as estimated separately from surveys in the second half of the twentieth century. The pattern of richer voters supporting Republicans has increased since 1970. The data used in the estimate for 1992 appear in Figure 13.2.$

Figure 13.4: Coefficient of income (on a 1<U+2013>5 scale) with $\pm 1$ standard-error bounds in logistic regressions predicting Republican preference for president, as estimated separately from surveys in the second half of the twentieth century. The pattern of richer voters supporting Republicans has increased since 1970. The data used in the estimate for 1992 appear in Figure 13.2.

13.3 Predictions and comparisons

로지스틱 회귀모델의 예측은 확률적이다. 따라서 관측되지 않은 미래의 데이터 관측치 $y^{new}_i$에 대해 우리는 점예측치보다 예측확률을 구하게 된다.

\[ p^{new}_i = \Pr(y^{new}_i = 1) = \text{logit}^{-1}(X^{new}_i\beta), \]

13.3.1 Point prediction using `predict`

소득 수준이 5점 척도 중에서 5점인 사람들의 투표 선호도를 예측하고자 한다고 할 때, 우리는 predict 함수를 이용하여 추정된 확률을 컴퓨팅할 수 있다.

new <- data.frame(income = 5)
pred <- predict(fit_1, type = "response", newdata = new)
pred

##         1 
## 0.4703885

predict 함수에서 type="response를 설정하면 확률 척도로 예측값을 구할 수 있다. 만약 type="link"로 설정할 경우에는 로짓 척도로 선형확률을 구할 수 있다.

invlogit(predict(fit_1, type="link", newdata=new))=new)는 predict(fit_1, type="response", newdata=new)와 같은 결과를 산출한다.

13.3.2 Linear predictor with uncertainty using `posterior_linpred`

선형회귀모델 결과에 posterior_linpred 함수를 사용하면 선형예측값, $X^{new}\beta$의 시뮬레이션된 값을 계산할 수 있다. 하지만 여기에서는 mvrnorm을 사용한다.

이 결과는 $a + b\times 5$에 대해 시뮬레이션된 사후분포를 보여준다. 하지만 우리는 이 값을 직접적으로 사용하기보다는 확률 척도로 변환한 예측값을 사용한다.

13.3.3 Expected outcome with uncertainty using `posterior_epred`

Gelman, Hill, and Vehtari (2020, 223)에서는 posterior_epred 함수를 사용할 것을 권하고 있지만, 이 리딩노트에서는 mvrnorm로 얻은 결과의 로그를 풀어주는, exp()로 동일한 결과를 얻고자 한다.

epred <- exp(linpred_out)/(1 + exp(linpred_out))
print(c(mean(epred), sd(epred)))

## [1] 0.46986695 0.02848966

pred

##         1 
## 0.4703885

prediction 함수로 구한 pred=0.470과 시뮬레이션으로 구한 결과, mean(epred)=0.469가 거의 일치하는 것을 확인할 수 있다.

13.3.4 Predictive distribution for a new observation using `posterior_predict`

posterior_predict 함수를 이용하면 소득 수준이 5일 경우에 나타날 수 있는 개별 유권자의 투표 선택과 그 불확실성을 보여주는 사후분포를 구할 수 있다.

13.3.5 Prediction given a range of input values

앞서는 소득 수준이 5일 때의 예측값을 구했지만, 새로운 관측치의 벡터에 대한 예측값 역시 구하는 것이 가능하다.

new_five <- data.frame(income=1:5)
pred_five <- predict(fit_1, type="response", newdata=new)
linpred_fiveout <- linpred %*% t(cbind(1, c(1:5)))
epred_five <- exp(linpred_fiveout)/(1 + exp(linpred_fiveout))
apply(epred_five, 2, mean);apply(epred_five, 2, sd)

## [1] 0.2352525 0.2856796 0.3425540 0.4046141 0.4698670

## [1] 0.02449276 0.01810651 0.01301085 0.01716431 0.02848966

각 소득 수준에 따른 예측확률을 구할 수 있다.

13.3.6 Logistic regression with just an intercept

절편만 가지고 선형회귀모델을 돌릴 경우에는 평균을오 추정하는 것과 같다. 만약 단 하나의 이항 예측변수를 가지고 선형회귀모델을 분석하면 그 결과는 각 이항 값에 따른 평균의 차이를 추정하는 것과 같다. 마찬가지로 절편만 가지고 로지스틱 회귀모델을 분석할 경우는 비율에 대한 추정과 같다.

50명의 피험자들에 대한 무작위 표본이 있고, 이중 10명이 특정 질병에 걸렸다고 하자. 이때, 질병에 걸릴 확률은 0.2라고 할 수 있고 표준오차는 $\sqrt{0.2\times 0.8/50}=0.06$이 된다. 따라서 이 로지스틱 회귀모델을 다음과 같이 수립할 수 있다.

y <- rep(c(0, 1), c(40, 10))
simple <- data.frame(y)
fit <- glm(y ~ 1, family=binomial(link="logit"), data=simple)
summary(fit)

## 
## Call:
## glm(formula = y ~ 1, family = binomial(link = "logit"), data = simple)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.6681  -0.6681  -0.6681  -0.6681   1.7941  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -1.3863     0.3536  -3.921 8.82e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 50.04  on 49  degrees of freedom
## Residual deviance: 50.04  on 49  degrees of freedom
## AIC: 52.04
## 
## Number of Fisher Scoring iterations: 4

이때, 우리는 예측값을 확률 척도로 바꿀 수 있다: $\text{logit}^{-1}(-1.38) = 0.20$. 마찬가지로 표준오차를 이용해서 신뢰구간-불확실성도 추정할 수 있다: $\text{logit}^{-1}(-1.38\pm 0.35) = (0.15, 0.26)$.

13.3.6.1 Data on the boundary

$y=0$이거나 $y=n$일 경우는 어떻게 될까? Gelman, Hill, and Vehtari (2020, 52)에서 논의한 바와 같이 전통적인 표준오차 공식에 따르면 극단적인 경우 0이 산출된다. 따라서 우리는 대신 $\hat p = (y+2)/(n+4)$일 때, 95% 신뢰구간, $\hat p \pm \sqrt{\hat p(1-\hat p)/(n +4)}$을 구할 수 있다. 다음의 예제를 보자.

y <- rep(c(0, 1), c(50, 0))
simple <- data.frame(y)
fit <- glm(y ~ 1, family=binomial(link="logit"), data=simple)
summary(fit)

## 
## Call:
## glm(formula = y ~ 1, family = binomial(link = "logit"), data = simple)
## 
## Deviance Residuals: 
##        Min          1Q      Median          3Q         Max  
## -2.409e-06  -2.409e-06  -2.409e-06  -2.409e-06  -2.409e-06  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)
## (Intercept)   -26.57   50363.54  -0.001        1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 0.0000e+00  on 49  degrees of freedom
## Residual deviance: 2.9008e-10  on 49  degrees of freedom
## AIC: 2
## 
## Number of Fisher Scoring iterations: 25

전통적인 방식으로 표준오차를 계산하게 되면 터무니없는 결과가 나오게 된다. 그렇다면 시뮬레이션을 이용하면 어떻게 될까?

fit <- stan_glm(y ~ 1, family=binomial(link="logit"), 
                data=simple, refresh = 0)
print(fit)

## stan_glm
##  family:       binomial [logit]
##  formula:      y ~ 1
##  observations: 50
##  predictors:   1
## ------
##             Median MAD_SD
## (Intercept) -4.6    1.2  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

이 경우 대략적인 95% 신뢰구간은 $\text{logit}^{-1}(-4.58\pm2\times1.14)=(0,0.09)$이 된다. 기존의 공식을 이용한 표준오차로는 구할 수 없었던 극단적인 관측치에서의 결과를 구할 수 있게 되는 것이다.

13.3.7 Logistic regression with a single binary predictor

하나의 더미변수를 갖는 로지스틱 회귀모델의 경우 비율을 비교하는 것과 같다. 예를 들면 모집단 A의 50명 중에서 양성이 10명일 확률인 표본의 비율과 모집단 B의 60명 중에서 20명이 양성일 확률인 표본의 비율을 비교하는 것이다.

x <- rep(c(0, 1), c(50, 60))
y <- rep(c(0, 1, 0, 1), c(40, 10, 40, 20))
simple <- data.frame(x, y)
fit <- glm(y ~ x, family=binomial(link="logit"), data=simple)
summary(fit)

## 
## Call:
## glm(formula = y ~ x, family = binomial(link = "logit"), data = simple)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.9005  -0.9005  -0.6681   1.4823   1.7941  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -1.3863     0.3536  -3.921 8.82e-05 ***
## x             0.6931     0.4472   1.550    0.121    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 128.91  on 109  degrees of freedom
## Residual deviance: 126.42  on 108  degrees of freedom
## AIC: 130.42
## 
## Number of Fisher Scoring iterations: 4

비율 차이에 대한 추론을 도출하려면 더미의 값, 0과 1에 대한 확률 척도의 예측값을 비교해보면 된다.

sim_coef <- MASS::mvrnorm(1000, mu = coef(fit), Sigma = vcov(fit))
pred <- sim_coef %*% cbind(1, c(0, 1))
epred <- exp(pred)/(1 + exp(pred))
diff <- epred[,2] - epred[,1]
mean(diff);sd(diff)

## [1] 0.3234994

## [1] 0.07591516

13.4 Latent-data formulation

로지스틱 회귀모델 결과는 관측되지 않은, 또는 잠재적(latent) 변수를 사용해서 직/간접적으로 해석할 수 있다.

\[ y_{i} = \begin{cases} 1 & \text{if }z_i>0\\ 0 & \text{if }z_i<0 \end{cases} z_i= X_i\beta + \epsilon_i \]

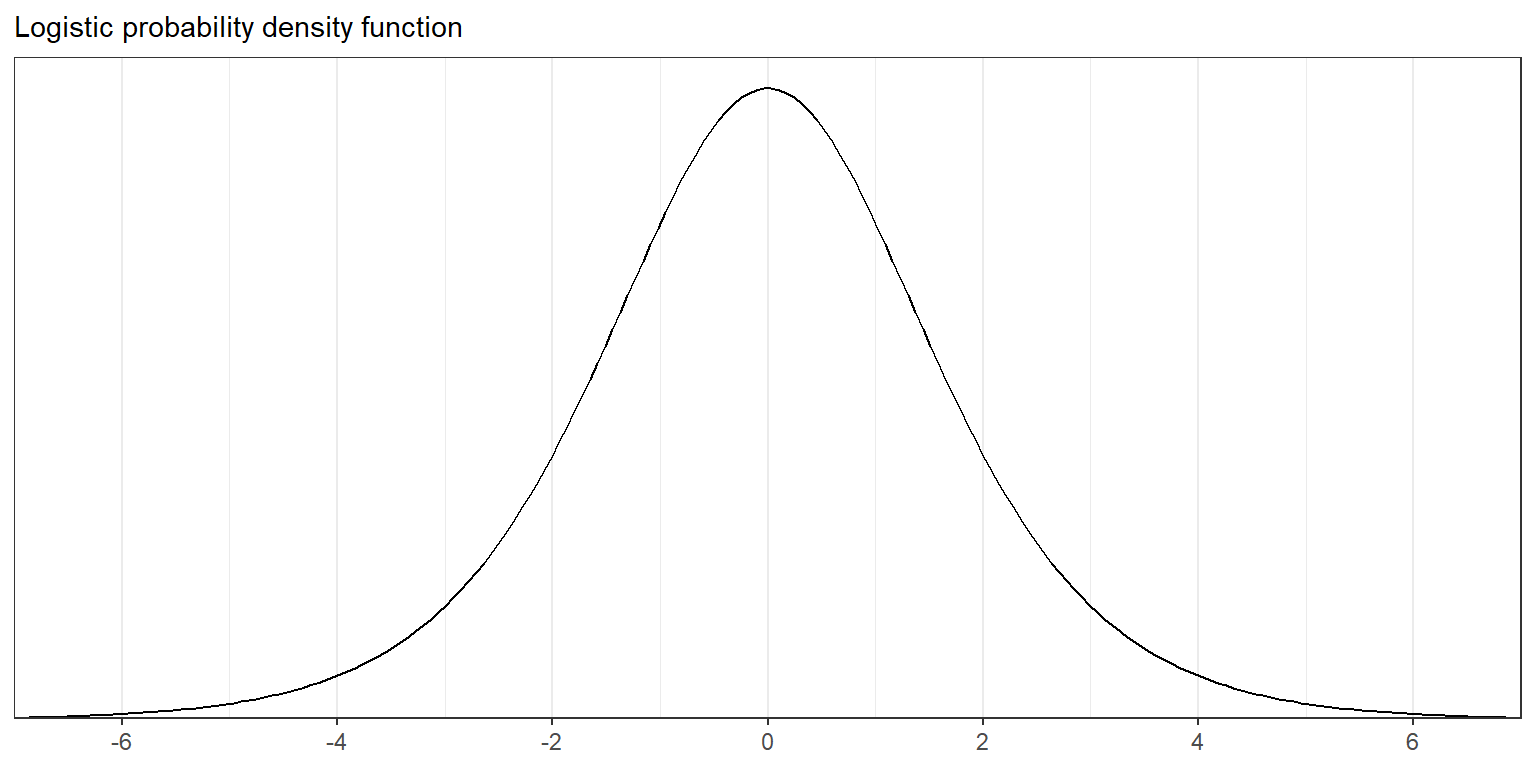
The probability density function of the logistic distribution, which is used for the error term in the latent-data formulation (13.5) of logistic regression. The logistic curve in Figure 13.1a is the cumulative distribution function of this density. The maximum of the density is 0.25, which corresponds to the maximum slope of 0.25 in the inverse logit function of Figure 13.1a.

Figure 13.5: The probability density function of the logistic distribution, which is used for the error term in the latent-data formulation (13.5) of logistic regression. The logistic curve in Figure 13.1a is the cumulative distribution function of this density. The maximum of the density is 0.25, which corresponds to the maximum slope of 0.25 in the inverse logit function of Figure 13.1a.

독립적인 오차 $\epsilon_i$이 로지스틱 확률분포를 가진다고 할 때, 위의 그래프는 다음과 같이 정의될 수 있다:

\[ \Pr(\epsilon_i<x)=\text{logit}^{-1}(x)\text{ for all }x. \]

따라서 $\Pr(y_i = 1) = \Pr(z_i > 0) = \Pr(\epsilon_i > -X_i\beta) = \text{logit}^{-1}(X_i\beta)$라고 할 수 있다.

다음의 그래프는 소득 수준, $x_i = 1$인 관측치 $i$의 선형예측값, $X_i\beta$를 설명하고 있다.

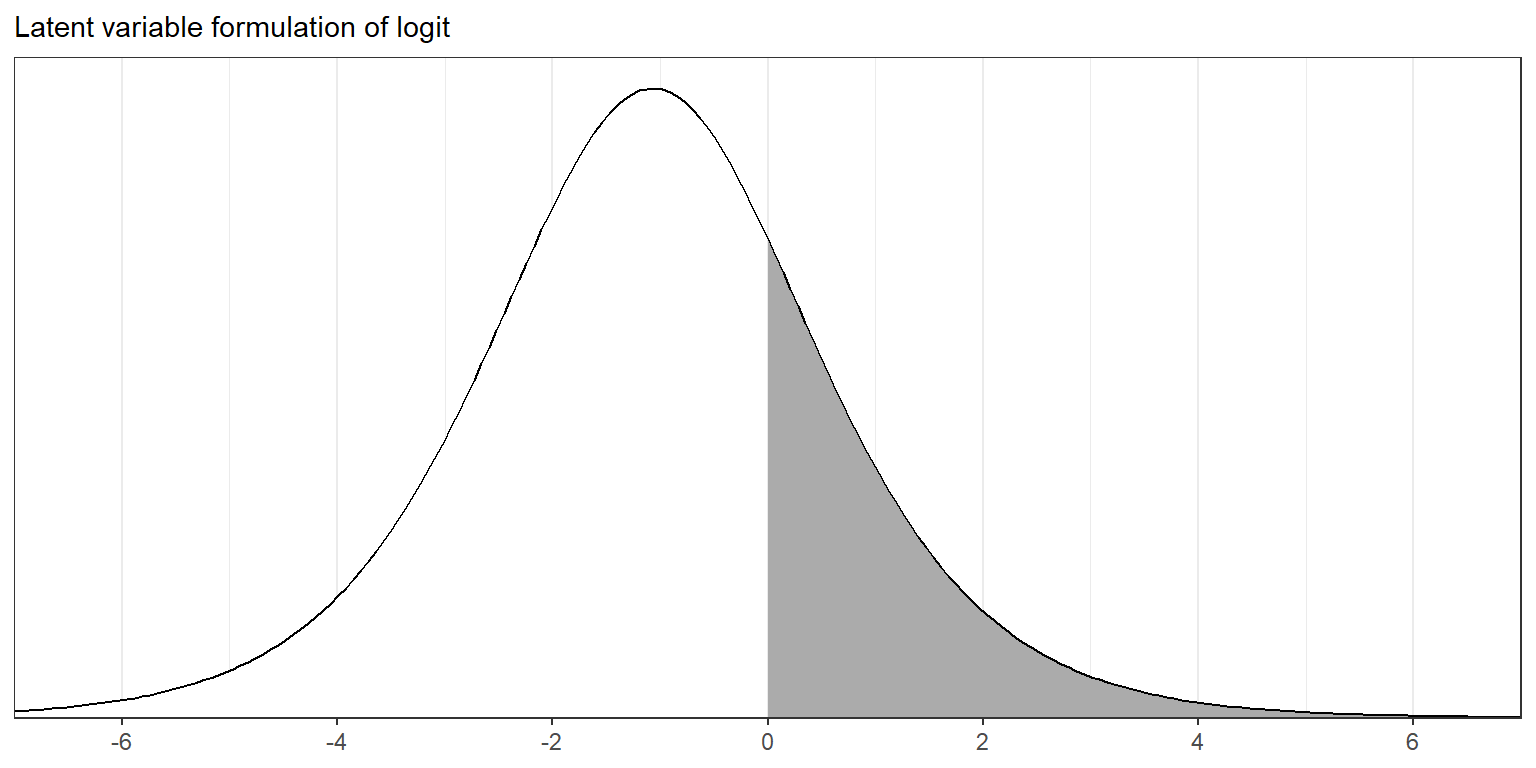
$The probability density function of the latent variable $z_i$ in model (13.5) if the linear predictor, $X_i\beta$, has the value <U+2212>1.07. The shaded area indicates the probability that $z_i > 0$, so that $y_i = 1$ in the logistic regression.$

Figure 13.6: The probability density function of the latent variable $z_i$ in model (13.5) if the linear predictor, $X_i\beta$, has the value <U+2212>1.07. The shaded area indicates the probability that $z_i > 0$, so that $y_i = 1$ in the logistic regression.

그래프의 곡선은 잠재적 변수 $z_i$의 분포를 보여주며, 음영은 $y_i = 1$일 때, $z_i > 0$인 확률을 나타낸다.

13.4.1 Interpretation of the latent variables

잠재변수는 일종의 컴퓨팅된 트릭에 가깝지만 실질적으로 해석될 수 있다. 예를 들어, 사전선거 설문조사에서 부시 지지자들을 $y_i= 1$이라고 하고 클린턴 지지자들을 $y_i = 0$이라고 하자. 관측되지 않은 연속형 변수 $z_i$는 클린턴에 비해 부시에 대한 응답자의 “효용”이나 선호로 해석될 수 있다.: 부호는 어떤 후보를 선호하는지에 대한 효용, 그리고 계수값의 크기는 그 선호의 강도를 보여준다는 것이다.

13.4.2 Nonidentifiability of the latent scale parameter

로지스틱 확률 밀도함수는 종 형태로 나타나며, 잠재변수 $z$에 대한 로지스틱 모델은 정규회귀모델에 거의 근사한다:

\[ z_i = X_i\beta + \epsilon_i,\: \epsilon_i\sim \text{N}(0, \sigma^2) \]

이 부분의 내용은 후에 프로빗 모델에 관련한 부분에서 자세하게 다룰 것이다.

13.5 Maximum likelihood and Bayesian inference for logistic regression

로지스틱 회귀모델에서는 대개 최대가능도, 베이지언 추론, 그리고 다른 정규화 기법의 순으로 추정 방법을 살펴보고는 한다.

13.5.1 Maximum likelihood using iteratively weighted least squares

$y_i = 0$ 또는 $y_i = 1$인 이항로지스틱 회귀모델의 경우 가능도는 다음과 같이 나타난다.

\[ p(y|\beta, X) = \prod^n_{i=1} \begin{cases} \text{logit}^{-1}(X_i\beta) & \text{if }y_i = 1\\ 1-\text{logit}^{-1}(X_i\beta) & \text{if }y_i = 0 \end{cases} \]

위의 가능도는 다음과 같이 바꾸어 쓸 수 있다.

\[ p(y|\beta, X) = \prod^n_{i=1}\Big(\text{logit}^{-1}(X_i\beta)\Big)^{y_i}\Big(1-\text{logit}^{-1}(X_i\beta)\Big)^{1-y_i} \]

가능도를 최대화하는 $\beta$를 찾기 위해서 가능도에 대한 도함수 $dp(y|\beta,X)/d\beta$를 컴퓨팅해, 이 도함수가 0이 되는 지점의 해(solution)가 $\beta$라는 것을 알 수 있다. 최대가능도 추정량(MLE)은 반복되는 최적화 알고리즘을 통해서 도함수의 결과가 0이되는 지점에서 찾을 수 있다.

13.5.2 Bayesian inference with a uniform prior distribution

모집단 모수(parameters)에 대한 사전분포가 단일한 형태(uniform)를 이룬다면, 사후밀도는 가능도 함수에 비례하며, 사후분포의 최빈값(사후밀도를 최대화하는 $\beta$ 계수의 벡터)은 MLE가 된다.

선형회귀모델에서 비정보 사전분포(noninformative prior)를 가지고 베이지언 추론을 할 경우의 이점은 전체 사후분포로부터 시뮬레이션을 이용하여 불확실성을 요약하여 보여줄 수 있고, 확률적 예측을 할 수 있다는 것에 있다.

13.5.3 Default prior in `stan_glm`

stan_glm은 디폴트 값으로 약한 정보를 가진 사전분포를 사용한다. 이 리딩노트에서는 stan_glm을 사용하지는 않기 때문에 간단하게 각 섹션의 내용을 요약하는 선에서 정리하도록 한다.

13.5.4 Bayesian inference with some prior information

사전분포에 대한 정보를 사용가능할 때, 우리는 추정량과 예측값의 정확성을 높일 수 있다. $\Pr(y_i=1) = \text{logit}^{-1}(a + bx)$인 로지스틱 회귀함수에서 제약이 약한 경우를 가정할 때, $b$의 값이 0부터 1 사이에 위치한다고 한다고 볼 수 있으며, 우리는 $b$에 대한 정규 사전분포를 평균 0.5, 표준편차 0.5, 즉 $b$가 0과 1 사이에 위치할 확률이 68%라고 할 수 볼 수 있다. 그리고 95%에 해당하는 $b$가 -0.5와 1.5 사이에 위치할 것이라고 기대할 수 있다.

13.5.5 Comparing maximum likelihood and Bayesian inference using a simulation study

사전분포의 역할을 이해하기 위해서 몇 가지 시나리오를 생각해보자. 진짜 모수의 값이 $a = -2$이고 $b=0.8$이라고 가정하고 데이터가 -1과 1 사이의 단일분포로부터 추출된 $x$의 값으로 이루어진 실험으로부터 얻어진 데이터라고 하자.

library("arm", "rstanarm")
bayes_sim <- function(n, a=-2, b=0.8){
  x <- runif(n, -1, 1)
  z <- rlogis(n, a + b*x, 1)
  y <- ifelse(z>0, 1, 0)
  fake <- data.frame(x, y, z)
  glm_fit <- glm(y ~ x, family=binomial(link="logit"), data=fake)
  stan_glm_fit <- stan_glm(y ~ x, family=binomial(link="logit"), data=fake,
                           prior=normal(0.5, 0.5), refresh = 0)
  display(glm_fit, digits=1)
  print(stan_glm_fit, digits=1)
}

표본규모를 이용해 시뮬레이션을 하고 $b$에 대한 추론에 집중해보자:

$n=0$. 전혀 새로운 데이터가 없을 때, 위의 함수는 돌아가지 않는다. 이때 사후분포는 사전분포와 똑같이 평균 0.5, 표준편차 0.5가 된다.
$n=10$. 10개의 관측치만 가지고 있을 때, MLE에는 잡음이 많고 우리는 베이지언 사후분포가 사전분포에 근접할 것이라고 기대하게 된다. 이때 베이즈 추정량은 0.7로 사전 분포의 평균인 0.5와 가깝게 나타난다. MLE는 2.1로 사전분포와 비교할 때, 꽤 잡음이 많이 포함된 것을 확인할 수 있다.

bayes_sim(10)

## glm(formula = y ~ x, family = binomial(link = "logit"), data = fake)
##             coef.est coef.se
## (Intercept) -2.7      1.6   
## x           -1.9      2.5   
## ---
##   n = 10, k = 2
##   residual deviance = 5.8, null deviance = 6.5 (difference = 0.7)
## stan_glm
##  family:       binomial [logit]
##  formula:      y ~ x
##  observations: 10
##  predictors:   2
## ------
##             Median MAD_SD
## (Intercept) -2.1    0.9  
## x            0.4    0.5  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

$n=100$. bayes_sim(100)이라고 하자. 이 경우 MLE 추정량은 다시 1.2로 꽤 극단적인 값을 보여준다. 하지만 베이즈 추정량은 사전분포의 평균 0.5에 근접한 것을 확인할 수 있다.

bayes_sim(100)

## glm(formula = y ~ x, family = binomial(link = "logit"), data = fake)
##             coef.est coef.se
## (Intercept) -2.4      0.4   
## x            1.0      0.7   
## ---
##   n = 100, k = 2
##   residual deviance = 58.2, null deviance = 60.5 (difference = 2.3)
## stan_glm
##  family:       binomial [logit]
##  formula:      y ~ x
##  observations: 100
##  predictors:   2
## ------
##             Median MAD_SD
## (Intercept) -2.4    0.4  
## x            0.7    0.4  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

$n=1000$. 마지막으로 1,000개의 관측치를 가진 실험을 시뮬레이션한다고 하자. 이 정도면 가능도 추정량도 꽤 믿을만하다고 볼 수 있을 것이다. 아래의 코드 결과는 베이즈 추정량과 MLE가 거의 차이가 없다는 것을 보여준다.

bayes_sim(1000)

## glm(formula = y ~ x, family = binomial(link = "logit"), data = fake)
##             coef.est coef.se
## (Intercept) -1.9      0.1   
## x            0.8      0.2   
## ---
##   n = 1000, k = 2
##   residual deviance = 774.7, null deviance = 799.0 (difference = 24.3)
## stan_glm
##  family:       binomial [logit]
##  formula:      y ~ x
##  observations: 1000
##  predictors:   2
## ------
##             Median MAD_SD
## (Intercept) -1.9    0.1  
## x            0.8    0.2  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

13.6 Cross validation and log score for logistic regression

예측과 일반화에 대한 모델의 성과를 평가하고자 할 때, 우리는 이항 관측치와 이항 예측치 간을 비교해서 맞게 예측한 비율을 계산할 수 있다. 단, 이 경우 예측확률에 있어서의 추가적인 정보는 완벽하게 무시하게 된다. 그리고 우리는 비선형 회귀모델의 경우 일탈도(deviance)를 이용해 일반화 선형모형에서 모형이 자료를 얼마나 잘 설명하지 못하는가를 보여주는데, 이 일탈도는 대개 로그값을 취한 가능도(log-likelihood)로 정의된다. Gelman, Hill, and Vehtari (2020, 230–31)은 LOO (leave-one-out) 절차를 통해 각 모델의 로그 예측확률을 컴퓨팅해서 살펴볼 것을 제안하고 있다.

13.6.1 Understanding the log score for discrete predictions

다음의 시나리오를 생각해보자: 추정된 모수, $\hat \beta$를 가지고 로지스틱 회귀모델을 적합하고 그 모델 결과를 $n^{new}$라는 새로운 데이터 관측치를 가지는 예측변수 행렬, $X^{new}$에 적용해 예측확률 $p^{new}_i = \text{logit}^{-1}(X^{new}_i\hat \beta)$ 벡터를 산출하는 것이다. 그리고 나서 결과인 $y^{new}$를 확인하고 모델의 적합도를 다음과 같은 통계량을 이용해 평가해보자.

\[ \text{out-of-sample log score} = \sum^{n^{new}}_{i=1} \begin{cases} \log p^{new}_i & \text{if }y^{new}_i = 1\\ \log (1-p^{new}_i) & \text{if }y^{new}_i = 0\\ \end{cases} \]

예측 로그값은 각 데이터 관측치의 예측 확률에 로그를 씌워 총합을 구한 것이다.

$p^{new}_i = 0.8$일 경우, 새로운 관측치 $y^{new}_i$가 1일 확률이 80%라는 것을 의미한다.
$p^{new}_i = 0.6$일 경우, 새로운 관측치 $y^{new}_i$가 1일 확률이 60%라는 것을 의미한다.
확률이 0.8인 모델에서 0.6인 모델이 될 때, 그 로그값은 $0.693n^{new}-0.587n^{new}=0.106n^{new}$으로 약 10 데이터 관측치에 따라 로그값이 1 정도 개선되었다는 것을 보여준다.

13.6.2 Log score for logistic regression

섹션 13.1의 1992년 미 대선 캠페인과 관련된 설문조사 예제를 떠올려보자. 그 설문조사는 중 빌 클린턴에 대한 지지를 표현한 702명의 응답자들과 조지 부쉬에 대한 선호를 나타낸 477명의 응답자들로 이루어졌다.

어떠한 예측에 추가적인 정보도 주어지지 않은 모델, 즉 각 후보에 대한 지지 확률이 0.5일 경우, 1179명의 응답자들에 대한 로그값은 $1179\log(0.5) = -817$이 된다.
만약 59.5%의 응답자가 클린턴을, 40.5%가 부시를 지지한다고 할 때, 우리는 각각의 값을 통해 로그값을 산출할 수 있다: $477 \log(0.405) + 702 \log(−.595) = −796$.
이 두 모델의 로그값 차이를 표본크기로 나누어줄 때, $(817-796)/1179 =0.018$, 우리는 추가된 정보가 얼마나 종속변수를 더 설명하는 데 도움을 주는지(개선하였는지)를 알 수 있다.

References

Gelman, Andrew, Jennifer Hill, and Aki Vehtari. 2020. Regression and Other Stories. Cambridge University Press.