Chapter 8 Fitting regression models

Gelman, Hill, and Vehtari (2020) 은 예제를 통해 실제로 통계모델을 데이터에 적용해보는 과정을 통해 단순선형회귀모델, 다중선형회귀모델, 비선형모델, 예측모델에 대한 적용과 인과추론에 대한 적용 등의 순으로 회귀분석 모델을 이해하는 데 초점을 두고 있다.

이 챕터는 회귀모델에 대한 추론의 수학적 구조에 관한 내용과 선형회귀모델의 추정법을 이해하는 데 도움이 되는 대수학(algebra)에 대해 살펴본다. 특히, 이 챕터에서 저자들은 stan_glm을 이용한 방법을 통해 전통적인 선형회귀모델과 베이지안 접근법에 입각한 모델 적합이 어떻게 다른지, 각 모델의 기저에 놓인 논리를 함께 설명하고 있다. 전반적으로 lm을 위주로 사용하여 이 책의 내용을 정리하고 있지만, 베이지안 접근법에 대해 숙지할 수 있는 기회라고 생각하여 이 챕터에서는 stan_glm을 함께 사용한 내용을 정리하고자 한다.

8.1 Least squares, maximum likelihood, and Bayesian inference

추론(inference)이란 무엇일까? 회귀모델을 추정하고 그 적합 결과의 불확실성을 평가하는 단계라고 할 수 있다.

• 데이터에 가장 잘 적합하는 계수값 \(a\)와 \(b\)의 값을 찾는 추정법인 최소자승법(least square)에서 시작한다.

• 다음으로는 최소자승법을 포함하여 로지스틱 회귀모델과 일반화 선형모델과 같은 내용들을 다루는 보다 일반적인 틀인 최대가능도(maximum likelihood)에 대해서 논한다.

• 마지막으로 사전정보(prior information)와 사후 불확실성(posterior uncertainty)에 대한 확률적 표현을 가능하게 하는 베이지안 추론(Bayesian inference)이라는 보다 일반적인 접근법을 학습한다.

8.1.1 Least squares

전통적인 선형회귀모델, \(y_i = a + bx_i + \epsilon_i\)에서 계수값 \(a\)와 \(b\)는 오차 \(\epsilon_i\)를 최소화하도록 추정된 값이다. 만약 관측치의 개수\((n)\)가 2보다 많다면, 일반적으로 데이터를 완벽하게 설명하는(perfect fit) 선을 찾기란 불가능하다.

• 데이터를 완벽하게 설명하는 회귀선이란 모든 관측치 \(i = 1, \dots, n\)에 대해 구축한 모델 \(y_i = a + bx_i\)에 오차가 존재하지 않는다는 것을 의미한다.

• 대개 추정의 목적은 잔차의 제곱합(sum of the squares of the residuals)을 최소화하는 추정값 \((\hat a, \hat b)\)를 찾는 것에 있다.

  • 이때, 잔차, \(r_i = y_i - (\hat a + \hat b x_i)\).

  • 다르게 말하면 개별 관측된 데이터 하나하나와 주어진 \(x\)를 모델에 투입해 예측한 값, \(\hat y\) 간의 차이를 말한다.

  • 모델이 예측력이 뛰어나다면 이 잔차의 크기는 매우 작을 것이다.

Gelman, Hill, and Vehtari (2020, 103) 은 잔차(\(\text{Residuals: }r_i = y_i - (\hat a + \hat b x_i)\))와 오차(\(\text{Errors: }\epsilon_i = y_i - (a + b x_i)\))를 구별한다.

• 모델은 오차로 쓰기도, 잔차로 쓰기도 한다.

  • 오차는 모집단 수준에서의 실제와 모델 간의 차이를 의미하며, 잔차는 표본 수준에서의 실제와 모델 간의 차이를 보여준다.

  • 즉, 모집단 수준의 모수인 오차는 또 다른 모수인 \(a\), \(b\)를 알지 못하듯, 알 수 없기에 계산할 수도 없다.

• 잔차의 제곱합(Residual sum of squares; RSS)은 다음과 같이 계산할 수 있다:

\[ \mathrm{RSS}= \sum^{n}_{i=1}(y_i - (\hat a + \hat b x_i))^2. \]

\(\mathrm{RSS}\)를 최소화하는 \((\hat a, \hat b)\)는 최소제곱 또는 일반화최소제곱(ordinary least squares), 또는 OLS 추정값이라고 불리며 다음과 같이 행렬 방식으로도 쓸 수 있다.

\[ \hat \beta = (X^t X)^{-1}X^t y. \]

• 이때 \(\beta = (a, b)\)는 계수값을 나타내는 벡터이고 \(X = (1, x)\)는 회귀모델에서 예측변수의 행렬을 의미한다.

  • 이 행렬에서 1은 1로 이루어진 열을 보여주는, 회귀모델의 상수항(constant term)으로 회귀모델을 추정할 때 기울기와 함께 절편값도 추정하므로 반드시 포함되어야 하는 열이다.

• 위의 행렬은 예측변수의 수가 몇이든 간에 최소자승 회귀모델에 적용할 수 있다. 일단 예측변수가 하나인 모델만 두고 보면 다음과 같이 기울기와 절편을 구할 수 있다.

\[ \begin{aligned} \hat b =&\frac{\sum^n_{i=1}(x_i-\bar x)y_i}{\sum^n_{i=1}(x_i-\bar x)^2}\\ \hat a =&\bar{y}-\hat b\bar x \end{aligned} \]

최소제곱 회귀선은 다음과 같이 나타낼 수 있다.

\[ y_i = \bar y + \hat b(x_i-\bar x) + r_i \]

이 회귀선은 \((\bar x, \bar y)\), 데이터의 평균을 지난다.

8.1.2 Estimation of residual standard deviation \(\sigma\)

회귀모델에서 오차 \(\epsilon_i\)는 평균이 0이고 표준편차가 \(\sigma\)인 분포를 따른다. 평균이 0인 것은 오차의 정의에 따른 것이고, 오차의 표준편차는 데이터로부터 추정될 수 있다.

• \(\sigma\)를 추정하는 가장 일반적인 방법은 잔차의 표준편차를 구하는 것이다: \(\sqrt{\frac{1}{n}\sum^n_{i=1}r^2_i} = \sqrt{\frac{1}{n}\sum^n_{i=1}(y_i-(\hat a + \hat b x_i))^2}\).

• 하지만 위와 같은 공식을 이용할 경우, 잔차의 제곱합을 최소화하기 위해 데이터에 기초해 \(\hat a\)와 \(\hat b\)를 구하기 때문에 과적합(overfitting)으로 인해 \(\sigma\)를 과소추정할 가능성이 크다.

• 이 과적합의 문제를 해결하기 위해, 빈도주의적 접근법에서는 잔차의 표준편차를 구할 때 \(n-2\)를 분포로 취하여 추정한다:

\[ \hat \sigma = \sqrt{\frac{1}{n-2}\sum^n_{i=1}(y_i - (\hat a + \hat b x_i))^2}. \]

위의 공식은 예측변수가 여러 개, 예를 들어 \(k\)개 일 때에 보다 일반적으로 사용될수 있다. 즉, \(y = X\beta + \epsilon\)은 \(n\times k\text{개의 예측변수인 행렬 }X\)는 다음과 같이 나타낼 수 있다.

\[ \hat \sigma = \sqrt{\frac{1}{n-k}\sum^n_{i=1}(y_i - (X_i\hat\beta))^2}. \]

8.1.3 Computing the sum of squares directly

공식에 따라서 최소자승법을 통한 계수값을 컴퓨팅으로 직접 추정할 수 있다.

1. 잔차의 제곱합(residual sum of squares)에 대한 rss의 함수를 작성한다.

rss <- function(x, y, a, b){ # x and y are vectors, a and b are scalars
resid <- y - (a + b*x)
return(sum(resid^2))
  }

rss 함수의 조건은 \(x\)와 \(y\)가 같은 길이의 벡터여야 하며, 결측치(NA)가 없어야 한다는 것이다.

• \((a, b) = (46.2, 3.1)\)을 최소자승법으로 구한 추정치라고 할 때, 잔차의 제곱합은 위의 함수로 평가할 수 있다: rss(hibbs$growth, hibbs$vote, 46.3, 3.0).

8.1.4 Maximum likelihood

선형모델로 구한 오차가 독립적이고 정규분포를 따른다면, 즉 \(y_i \sim N(a+bx_i, \sigma^2)\)라고 하면 최소자승법으로 구한 \((a, b)\)에 대한 추정값은 최대가능도 추정치(maximum likelihood estimate; MLE)가 된다.

• 회귀모델에서 가능도 함수(likelihood function)는 주어진 모수와 예측변수로 이루어진 데이터의 확률 밀도로 정의된다.

\[ \Pr(y|a, b, \sigma, X) = \prod^{n}_{i=1}\mathrm{N}(y_i|a + bx_i, \sigma^2) \]

이때, 가능도 함수에서 \(\mathrm{N(\cdot|\cdot, \cdot)}\)은 정규확률밀도 함수이다:

\[ \mathrm{N}(y|m, \sigma^2) = \frac{1}{2\pi\sigma}\mathrm{exp}\bigg(-\frac{1}{2}\Big(\frac{y-m}{\sigma}\Big)^2\bigg). \]

첫 번째, 가능도 함수는 가능도를 최대화하는 것의 필요조건이 잔차의 제곱합을 최소화하는 것이라는 의미이다. 따라서 최소자승법으로 구한 추정치 \(\hat \beta = (\hat a, \hat b)\)는 정규분포를 가정한 모델에서 최대가능도 추정값으로 간주할 수 있다.

일반적인 OLS로 잔차의 표준편차를 구했을 때와, \(\sigma\)에 대한 최대가능도 추정량을 구했을 때의 차이는 아래의 두 식에서 구별할 수 있다:

\[ \begin{aligned} \text{OLS: }&\hat \sigma = \sqrt{\frac{1}{n-2}\sum^n_{i=1}(y_i - (\hat a + \hat b x_i))^2}\\ \text{MLE: }&\hat \sigma = \sqrt{\frac{1}{n}\sum^n_{i=1}(y_i - (\hat a + \hat b x_i))^2} \end{aligned} \]

즉, MLE로 구할 때에는 예측변수의 개수에 따른 일종의 조정이 이루어지지 않는다는 것을 확인할 수 있다. 그렇다면 OLS에 비해 MLE로 조건이 동일한 상황에서 선형회귀모델을 추정할 경우, MLE는 \(\hat \sigma\)를 미세하게 과소추정할 수 있다(분모가 조금 더 크니까; \(n > n-2\)).

베이지안 추론에서는 모델의 각 파라미터에 대한 불확실성이 자동적으로 다른 모수들의 불확실성을 설명한다. 베이지안 추론의 이와 같은 속성은 예측변수의 수가 많을 경우 분석의 장점을 가지며 보다 복잡하거나 위계성을 가진 모델을 추정할 때 유리하다.

8.1.5 Where do the standard errors come from? Using the likelihood surface to assess uncertainty in the parameter estimates

최대가능도추정법에서 가능도 함수는 최대가능도 추정량이 가장 클 때를 보여주는 역할을 수행한다고 볼 수 있다.

fit8.1 <- lm(vote ~ growth, data = hibbs)
arm::display(fit8.1)

## lm(formula = vote ~ growth, data = hibbs)
##             coef.est coef.se
## (Intercept) 46.25     1.62  
## growth       3.06     0.70  
## ---
## n = 16, k = 2
## residual sd = 3.76, R-Squared = 0.58

Figure 8.1은 계수값 \(a\)와 \(b\)에 대한 함수로 가능도의 예제를 보여준다. 엄밀하게 말하면, 이 모델은 세 개의 파라미터(\(a, b, \sigma\))를 가지고 있다. 그러나 간명하게 보여주기 위하여 추정된 \(\hat \sigma\)의 조건 하에서 \(a\)와 \(b\)의 가능도를 보여주었다.

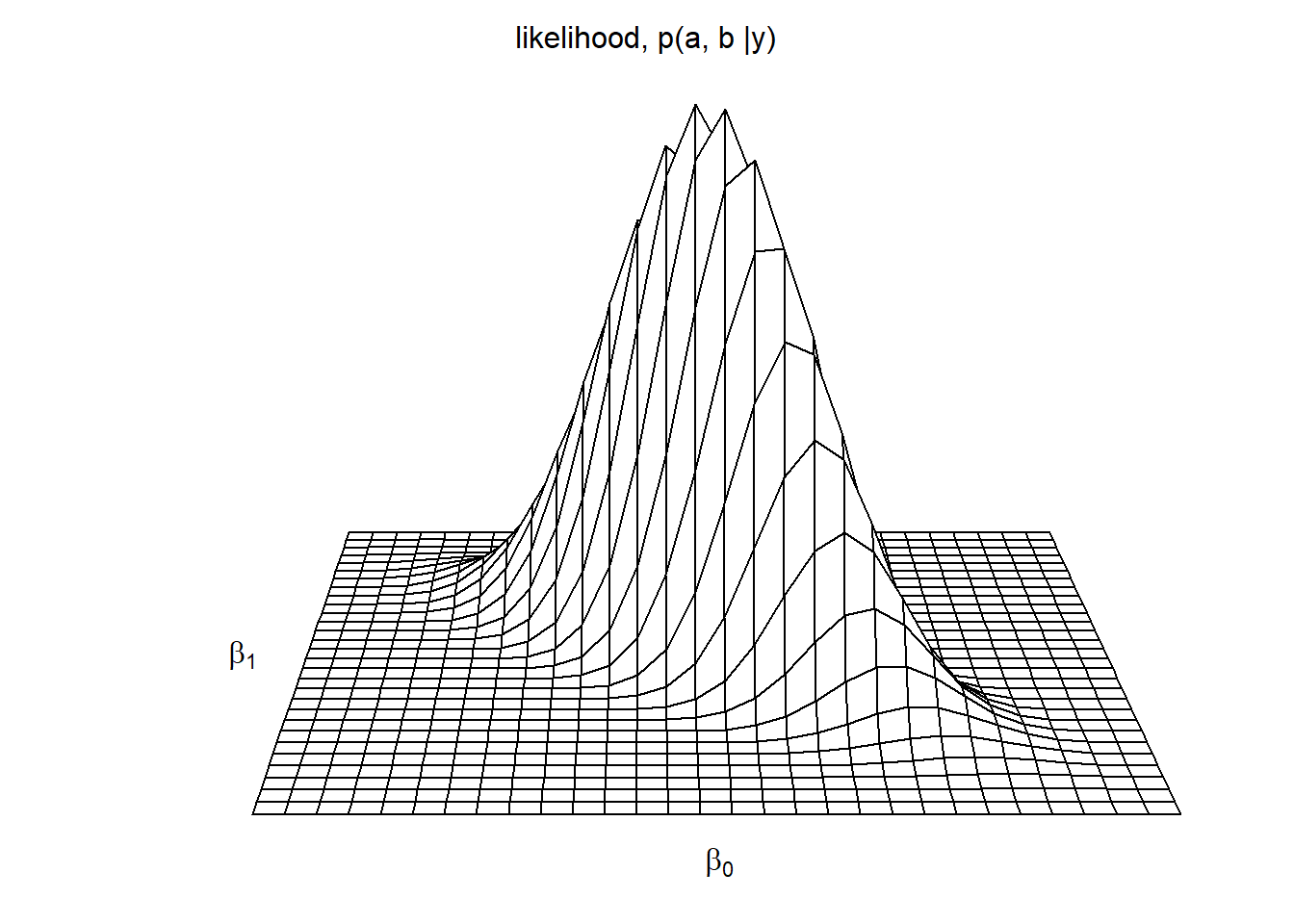
Figure 8.1: Likelihood function for the parameters \(a\) and \(b\) in the linear regression \(y = a + bx + \text{error}\), of election outcomes, \(y_i\) , on economic growth, \(x_i\).

Figure 8.2a는 \((\hat a, \hat b) = (46.2, 3.1)\)가 최대가능도 추정값이라는 것을 보여준다. Figure 8.1에서 가능도가 최고였을 때의 값, \(a\)와 \(b\)인 것이다. Figure 8.2a는 파마리터에 대해 \(\pm 1\) 표준오차에서의 불확실성도 함께 보여주고 있다.

가능도 함수는 최대값과 범주만 가지는 것이 아니라 상관관계도 가지고 있다. 가장 큰 가능도를 둘러싼 영역(area)은 Figure 8.2b에서와 같이 나타낼 수도 있다. 불확실성의 타원 형태는 우리로 하여금 데이터에 대한 정보나 두 파라미터의 결합에 관한 모델의 정보를 제시한다. 여기에서는 두 파라미터 값은 부의 상관관계를 가진다.

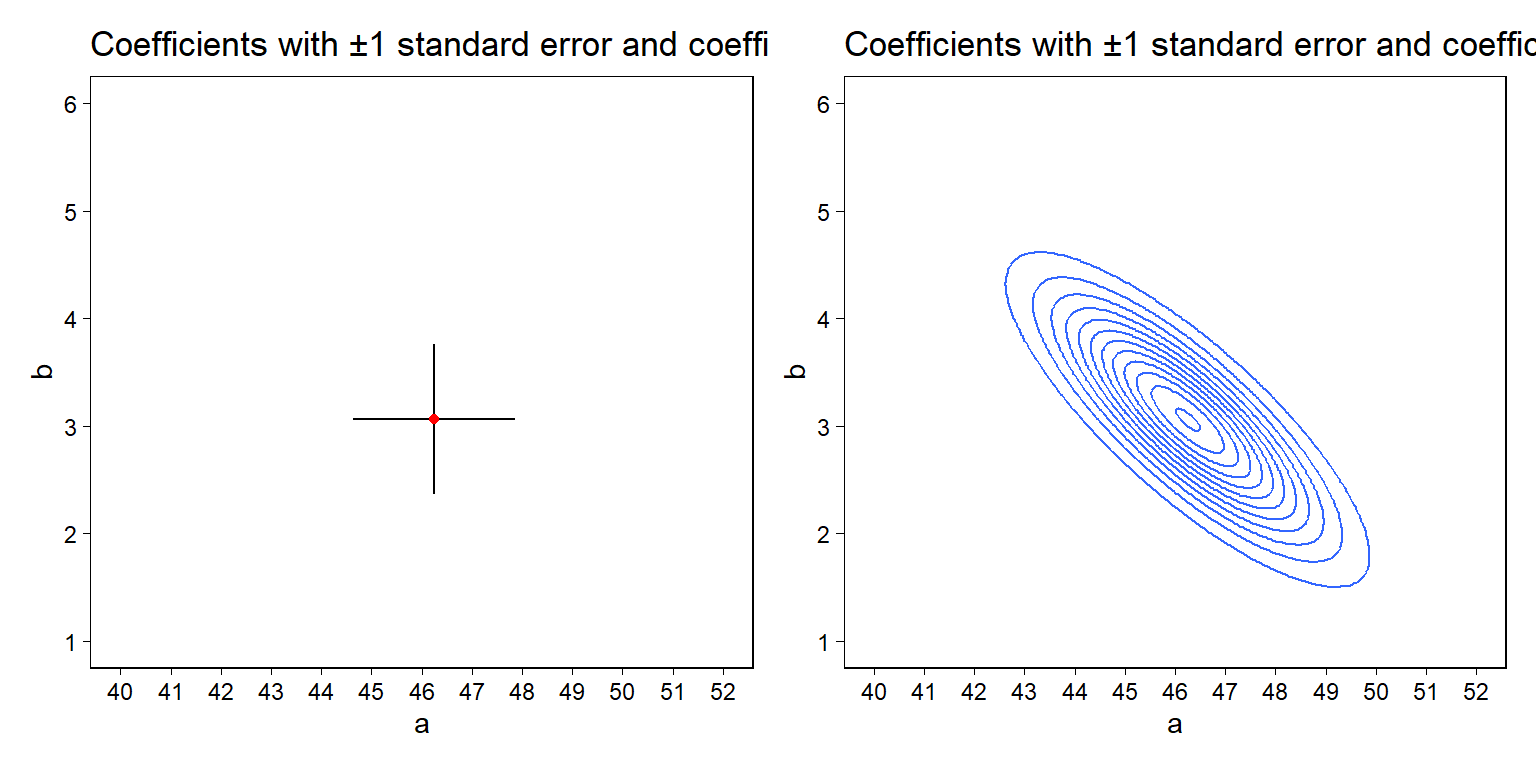
Figure 8.2: (a) Mode of the likelihood function (that is, the maximum likelihood estimate \((\hat a, \hat b)\)) with \(\pm 1\) standard error bars shown for each parameter. (c) Mode of the likelihood function with an ellipse summarizing the inverse-second-derivative-matrix of the log likelihood at the mode.

추론적 상관관계를 이해하기 위해서 산포도와 회귀선을 하나의 플롯으로 그려보았다. Figure 8.3b는 데이터에 따른 선의 가능한 범위를 보여준다. 즉, 시뮬레이션을 통해 표본이 다를 때 나타날 수 있는 선의 가능한 형태들을 함께 보여준다고 이해할 수 있다.

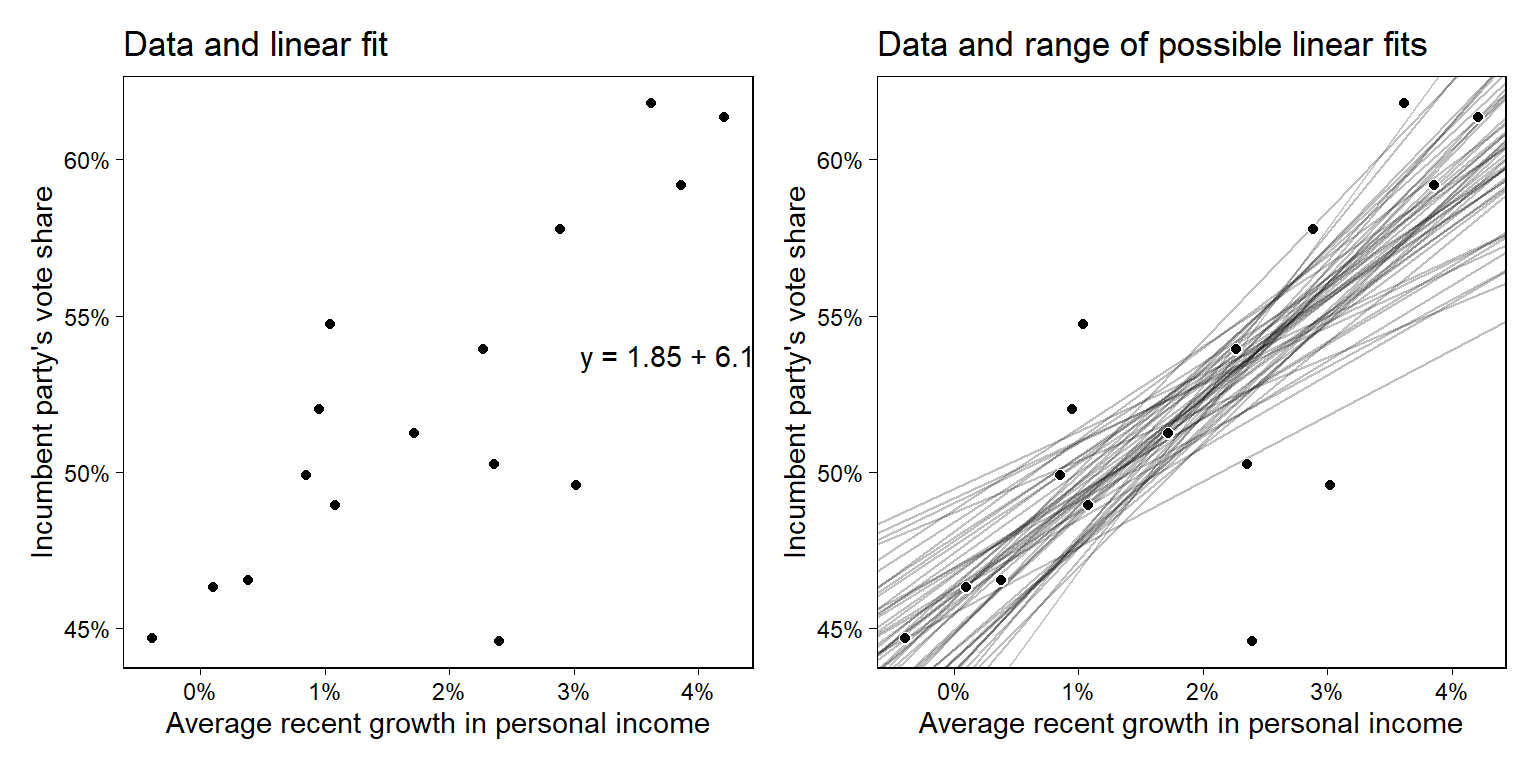
Figure 8.3: (a) Election data with the linear fit, \(y = 46.3 + 3.0x\), repeated from Figure 7.2b. (b) Several lines that are are roughly consistent with the data. Where the slope is higher, the intercept (the value of the line when \(x = 0\)) is lower; hence there is a negative correlation between a and b in the likelihood.

8.1.6 Bayesian inference

최소자승법이나 최대가능도는 데이터에 최적합하는 모수값을 찾지만 적합하는 방식 그 자체를 제약하거나 혹은 어떠한 방식으로 유도하지는 않는다. 하지만 Section 9.3에서 더 자세히 논의하겠지만, 베이지안 접근법은 모델에 포함되는 모수값에 대한 사전정보를 가진다. 베이지안 추론은 모수에 대한 외부적 정보를 확률적으로 보여주는 사전분포에 대한 가능도와 곱하는 식으로 사전 정보와 데이터 간의 일종의 조정한 결과를 산출하는 접근법을 취한다. 이와 같이 가능도와 사전분포를 결합한 결과로 얻어지는 것을 사후분포(posterior distribution)이라고 하며, 사후분포는 데이터를 본 이후에 모수에 대한 우리의 지식을 요약해서 보여준다.

• 즉, 간단하게 얘기하면 빈도주의가 모수는 어떤 분포에서 도출되었다는 모집단에 대한 가정에서 시작하는 반면, 베이지언 접근법은 그러한 가정을 일종의 사전정보로 받아들이고 실제로 관측하는 데이터에 대한 정보를 그 사전정보와 결합시켜 나가며 사후분포를 산출해 나가는 것이다.

• 앞서 언급한 바와 같이 사후분포는 가능도 함수로부터 유도된 것이다.

최대가능도추정법을 일반화하면 제한된 최대가능도 추정법(maximum penalized likelihood estimation)이라고 할 수 있는데, 이는 사전분포를 일종의 “제약 함수”(penalty function)으로 간주하여 모수를 잘 반영하지 않는 값에 대한 가능도를 일종의 저평가(downgrade)하는 것이다. 다른 말로 사전분포와 데이터에서만 얻은 것 사이의 어딘가를 추정하는 것이다. 사전분포를 고정시키기 때문에 제한된 최대가능도 추정량은 순수 최대가능도 또는 최소자승법 추정량에 비해 더 안정적일 수 있다.¹⁷

사전정보를 더하는 것 외에도 베이지언 추론은 확률에 대한 불확실성을 표현한다는 점에서 빈도주의적 접근과 차이가 있다. 예를 들어 stan_glm을 통해 모델을 적합할 때, 우리는 사후분포를 보여주는 일련의 시뮬레이션 추출 결과를 얻을 수 있고, 그 사후분포의 중앙값, 중앙값 절대편차, 시뮬레이션에 기초한 불확실성 구간 등을 요약해서 제시할 수 있다.

Gelman, Hill, and Vehtari (2020) 이 베이지안 방법을 선호하는 이유는 확률과 시뮬레이션을 이용한 불확실성의 표현이 보다 유연하다는 것과 사전정보를 추론에 포함하는 것을 바탕으로 안정적 추론이 가능하다고 보기 때문이다.

8.1.7 Point estimate, mode-based approximation, and posterior simulations

데이터에 전반적으로 최적합하는 계수값의 벡터인 점추정량(point estimate)는 최소자승법으로 구한 해(solution)이다. 베이지언 모델에서는 이 점추정량에 해당하는 것이 데이터와 사전분포에 전반적으로 최적합하는 사후 최빈값(posterior mode)라고 할 수 있다.

하지만 우리가 원하는 것은 추정량뿐만이 아니다. 추정량을 둘러싼 불확실성도 알고자 하는데, 이는 빈도주의적 접근처럼 표준오차의 개념으로 접근할 수 있지만 베이지언에서는 다변량 불확실성으로 나타나는 확률분포를 통해 시뮬레이션된 추정량의 사후분포를 얻을 수 있기 때문에 분위값으로 직접 제시할 수 있게 된다.

8.2 Influence of individual points in a fitted regression

얼마나 \(y_i\)의 변화가 \(\hat b\)의 변화로 이어지는지를 통해 데이터의 개별 관측치의 영향력을 살펴본다. \(y_i\)에서의 1 증가로 나타나는 \(\hat b\)에서의 변화를 \((x_i - \bar x)\)에 대한 비율로 나타낸다.

• 만약 \(x_i = \bar x\)라면, 회귀계수에 대한 \(i\)의 영향력은 0이다.

  • 왜냐하면 \((\bar x - \bar x) = 0\)이니까.

• \(x_i > \bar x\)이면, \(i\) 지점에서의 관측치는 정의 영향력(positive influence)을 가지고 있고, \(x_i\)가 평균으로부터 멀어질수록 \(x_i\)의 영향력이 커진다고 할 수 있다.

• \(x_i < \bar x\)이면, \(i\) 지점에서의 관측치는 부의 영향력(negative influence)을 가지고 있고, \(x_i\)가 평균으로부터 멀어질수록 \(x_i\)의 절대적인 영향력이 커진다고 할 수 있다.

Figure 8.4는 회귀분석에 있어서 개별 관측치의 영향력을 이해하는 시각화의 방법을 보여준다. 회귀계수 \(\hat \beta\)에 대해 추정된 벡터는 데이터 벡터 \(y\)와 일반화 선형모델의 선형 함수에 따라 산출된 결과인 것이다.

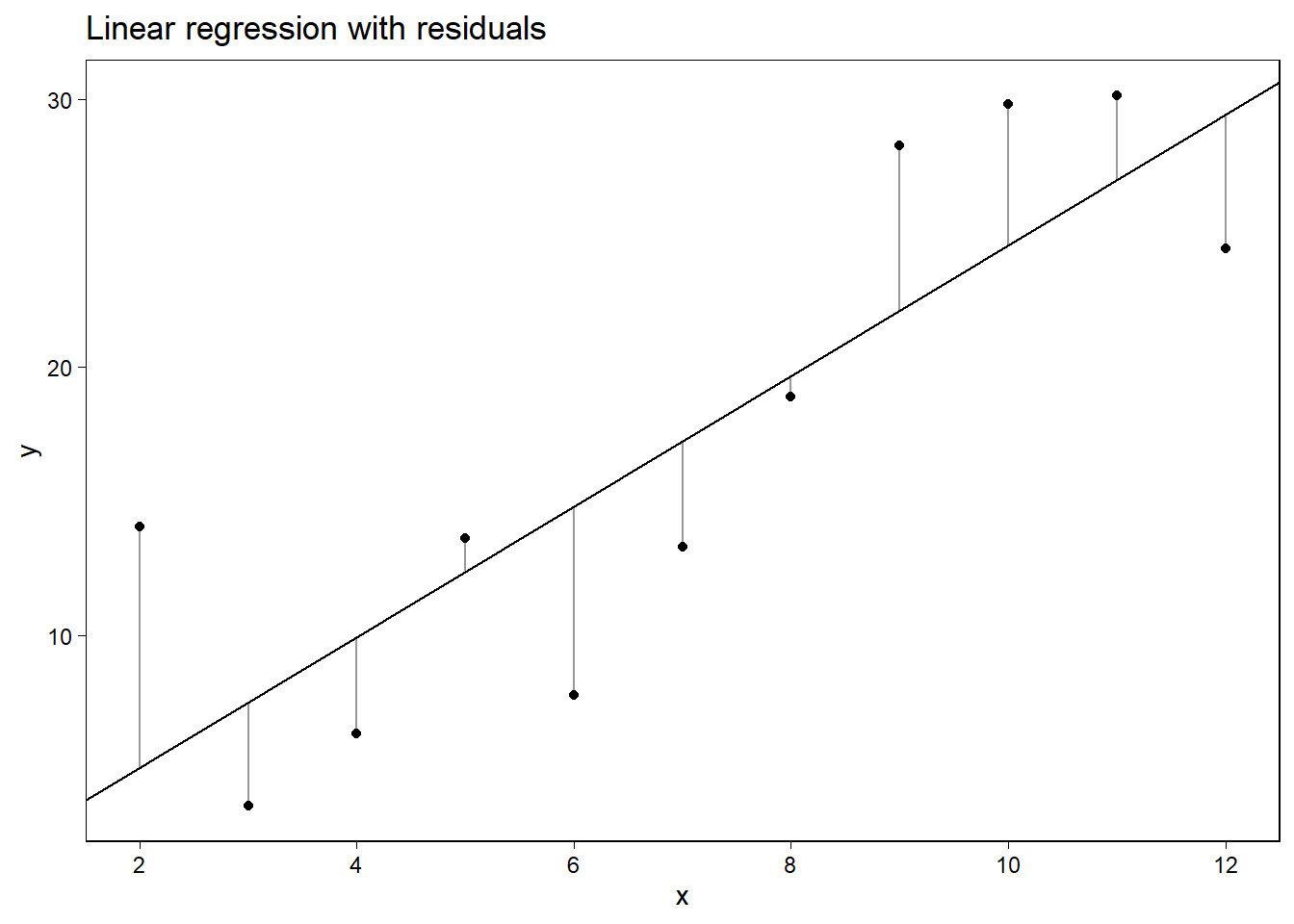
Figure 8.4: Understanding the influence of individual data points on the fitted regression line. Picture the vertical lines as rubber bands connecting each data point to the least squares line. Take one of the points on the left side of the graph and move it up, and the slope of the line will decrease. Take one of the points on the right side and move it up, and the slope will increase. Moving the point in the center of the graph up or down will not change the slope of the fitted line.

8.3 Least squares slope as a weighted average of slopes of pairs

회귀모델 \(y = a + bx + \text{error}\) 중 \(x\)가 더미변수일 때, 최소자승법으로 구한 추정값, 계수 \(b\)는 \(x\)가 0일 때와 1일 때, 각 집단의 결과변수의 평균 차이이다: \(\bar y_1 - \bar y_0\).

\(x\)가 연속형일 경우에는 기울기의 가중평균으로 추정된 \(\hat b\)를 나타낼 수 있다:

\[ \text{slope}_{ij} = \frac{y_j - y_i}{x_j - x_i}. \]

최적합하는 회귀곡선의 기울기는 개별 곡선들의 평균으로 정의된다. 관측치가 있다고 할 때, \(i\)와 \(j\)라고 할 수 있는 두 관측치 간의 선, 그 기울기를 모든 관측치를 대상으로 구한 뒤 그 평균을 구하는 것이다. 그리고 그 때, 그 평균을 \((x_j - x_i)^2\), 두 값의 차이에 제곱(음수 부호를 없애주는 과정)한 값으로 가중치를 부여하는 것이다.

\[ \begin{aligned} \text{weighted average of slopes}&=\frac{\sum_{i,j}(x_j-x_i)^2\frac{y_j-y_i}{x_j-x_i}}{\sum_{i,j}(x_j-x_i)^2}\\ &=\frac{\sum_{i,j}(x_j-x_i)(y_j-y_i)}{\sum_{i,j}(x_j-x_i)^2} \end{aligned} \]

8.4 Comparing two fitting functions: lm and stan_glm

R에서 선형회귀모델을 추정하는 두 가지 방법:

• lm: 전통적인 최소자승법을 사용한 회귀분석모델로 추정량과 표준오차를 적합하는 함수이다.

• stan_glm: 베이지언 추론으로 분석하며, 추정량과 표준오차, 그리고 사후 시뮬레이션을 제시한다.

stan_glm을 사용하는 두 가지 이유:

1. stan_glm으로 자동적으로 컴퓨팅되는 시뮬레이션 결과는 불확실성을 제시함으로써 현재 우리가 가진 데이터, 앞으로 가지게 될 데이터, 그리고 모수에 대한 어떤 함수든 간에 표준오차와 예측분포를 얻을 수 있게 해준다.

2. 시뮬레이션을 통한 베이지언 추론은 더 안정적인 추정량과 사전정보를 포함한 예측을 제시한다.

베이지언 추론은 데이터가 빈약하거나(small-n), 강한 사전정보가 있을 때, 빈도주의적 접근과는 다른 결과를 가져올 가능성이 높다. 또한 모델이 복잡하거나 위계성을 가지고 잇을 경우에는 전통적 접근과 베이지언 추론 간 결과 차이가 있을 수 있다.

8.4.1 Reproducing maximum likelihood using stan_glm with flat priors and optimization

베이지언 추정량과 전통적인 추정량(빈도주의적 추정량)을 한 번 R 코드로 살펴보자. mydata라는 데이터가 있다고 하자.

stan_glm(y ~ x, data = mydata)

사전정보가 설정되지 않은 채로 stan_glm()를 돌리면, 디폴트로 약한 사전정보(계수값이 0에 수렴한다는)를 가지고 회귀모델을 적합한다.

• 전통적 추론에 가까운 결과를 얻고 싶으면 평탄한 사전정보(flat prior)를 사용할 수 있고, 이 경우 사후분포는 가능도와 같아진다. 아래의 코드를 보자.

stan_glm(y ~ x, data=mydata, 
         prior_intercept=NULL, prior=NULL, prior_aux=NULL)

stan_glm의 세 파라미터에 NULL을 부여했다는 것은ㅇ 각기 절편, 계수값, 그리고 \(\sigma\) 모두에 평탄한 사전정보(각각이 서로 다르다거나 특정한 값을 가진다는게 아니라 무던~하다는)를 부여했다는 것을 의미한다.

그리고 stan_glm으로 기존의 lm과 가까운 결과를 얻고 싶다면 표집(sampling) 대신에 최적화(optimization)를 하면 된다. 그 결과는 제한 최대가능도 추정량을 산출하기 때문이다.

stan_glm(y ~ x, data=mydata, 
         prior_intercept=NULL, prior=NULL, prior_aux=NULL,
         algorithm="optimizing")

8.4.2 Running lm

확률적 예측 필요없이 최대가능도 추정량만 필요하다고 하면 R의 lm() 함수로 추정하면 된다.

lm(y ~ x, data = mydata)

8.4.3 Confidence intervals, uncertainty intervals, compatibility intervals

신뢰구간이란 기본적으로 추론의 불확실성을 보여주는 것이다. 불편향(unbiased), 정규분포된 추정량에 대한 가정을 바탕으로 그 추정량으로부터 \(\pm 1\) 표준오차에 약 68%의 확률로 모수의 진실값을 포함할 확률이 높다고 보는 것이며, \(\pm 2\) 표준오차에는 95% 확률로 그러할 것이라고 생각하는 것이다.

선형회귀모델에 있어서 잔차의 표준편차인 \(\sigma\) 그 자체는 오차로 추정된다. 만약 \(k\)개의 회귀계수를 갖는 회귀모델이 \(n\)개의 데이터 관측치에 대해 적합하고자 한다면, \(n-k\) 자유도를 가진다고 할 수 있으며, 이때 회귀계수에 대한 신뢰구간은 \(t_{n-k}\) 분포에 따라 구할 수 있다.

만약 stan_glm으로 적합한다면 68%와 95% 신뢰구간 각각은 중위값에 \(\pm 1, \pm 2\)에 해당하는 중위값 표준편차 값을 구해주면 되고, 이 경우에 시뮬레이션을 통해 직접 그 구간을 산출할 수 있다. 예제를 한 번 살펴보자.

x <- 1:10
y <- c(1,1,2,3,5,8,13,21,34,55)
fake <- data.frame(x, y)
fit <- stan_glm(y ~ x, data=fake, refresh = 0)
print(fit)

## stan_glm
##  family:       gaussian [identity]
##  formula:      y ~ x
##  observations: 10
##  predictors:   2
## ------
##             Median MAD_SD
## (Intercept) -13.4    6.8 
## x             5.1    1.1 
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 9.9    2.5   
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

그리고 이 결과로부터 시뮬레이션을 추출할 수 있다.

sims <- as.matrix(fit)
head(sims, n = 20)

##           parameters
## iterations (Intercept)        x     sigma
##       [1,]  -3.8449564 3.475038  8.672660
##       [2,]  -1.9260153 3.112200  9.016874
##       [3,] -21.9069149 6.176655  8.969247
##       [4,] -22.8506122 6.476414  8.811992
##       [5,] -13.2238727 5.607535  7.529085
##       [6,] -10.1305772 4.124203  6.679642
##       [7,] -17.4239561 5.901466 11.963498
##       [8,]  -2.2007477 3.239140 10.885391
##       [9,]  -3.0689087 3.474375 11.093255
##      [10,] -15.7840689 5.101348 10.520168
##      [11,]  -9.5194438 3.396553  8.755429
##      [12,] -12.4910217 3.895171  8.923379
##      [13,] -38.6189464 7.996241 24.078604
##      [14,] -39.9440771 8.035341 21.344225
##      [15,] -31.8740525 7.211540 20.329915
##      [16,] -24.4038354 6.208415 10.279084
##      [17,] -10.4630620 4.980395  9.864549
##      [18,] -10.9709236 4.639559 10.787506
##      [19,]  -5.5585543 3.733700  9.888777
##      [20,]   0.8256187 2.690757 10.205194

이때, 이 시뮬레이션 결과는 세 개의 열을 포함하는데 각각 절편, \(x\)에 대한 계수값, 그리고 잔차의 표준편차 \(\sigma\)에 대한 시뮬레이션 결과이다. 95% 구간을 추출하기 위해서는 다음의 코드를 사용하면 된다.

quantile(sims[,2], c(0.025, 0.975));

##     2.5%    97.5% 
## 2.614573 7.519634

quantile(sims[,"x"], c(0.025, 0.975))

##     2.5%    97.5% 
## 2.614573 7.519634

모든 신뢰구간은 불확실성을 보여주는 구간이라고 볼 수 있으며, 추정된 통계량에 대한 불확실성을 보여준다.

References

Gelman, Andrew, Jennifer Hill, and Aki Vehtari. 2020. Regression and Other Stories. Cambridge University Press.

---

17. 현 시점에서는 굳이 알아둘 필요는 없어 보인다.↩︎