Chapter 3 Some Basic Methods in Mathematics and Probability

회귀모델에 있어서 기초적인 수리통계학적 기법들을 숙지하는 것은 약 세 가지 측면에 있어서 중요하다.

1. 선형대수(linear algebra)와 간단한 확률분포는 정교한 모델의 토대가 된다.

2. 모델들을 들여다보기에 앞서 추론에 대한 기본적인 개념들을 이해하는 것은 유용하다.

3. 때로는 정교한 모델을 적합하기 이전에 연구문제의 일부에 대해 빠르게 비교 및 추정해보는 것은 모델 결과를 이해하는 데 유용하다.

3.1 Weighted averages

통계학에서 연구하고자 하는 모집단(target population)에 맞추기 위하여 데이터 또는 추론에 어떠한 가중치를 부여하는 것은 흔한 일이다. 간단한 예로, 2010년에 북미에 거주하는 4,560만명 중 3억 1000만명은 미국에, 1억 1200만명은 멕시코에, 3,400만명은 캐나다에 거주하는 사람이었다고 하자. 해당 연도에 각 국가에 거주하는 사람들의 평균 연령은 Table 3.1에서 확인할 수 있다. 그리고 모든 북미 거주자의 평균연령은 가중평균(weighted average)이다.

\[ \begin{align*} \text{average age} & = \frac{310{,}000{,}000 \cdot 36.8 + 112{,}000{,}000 \cdot 26.7 + 34{,}000{,}000 \cdot 40.7}{310{,}000{,}000 + 112{,}000{,}000 + 34{,}000{,}000} \\ & = 34.6. \end{align*} \]

단순평균이 아니라 가중평균이라고 하는 이유는 각 국가의 인구에 가중치(weights), 36.8, 26.7, 40.7, 를 비례하여 곱해주었기 때문이다. 북미의 전체 인구는 \(310 + 112 + 34 = 456\), 즉 4억 5,600만명이고, 우리는 위의 식을 다음과 같이 바꾸어 쓸 수 있다.

\[ \begin{align*} \text{average age} & = \frac{310{,}000{,}000}{456{,}000{,}000} \cdot 36.8 + \frac{112{,}000{,}000}{456{,}000{,}000} \cdot 26.7 + \frac{34{,}000{,}000}{456{,}000{,}000} \cdot 40.7 \\ & = 0.6798 \cdot 36.8 + 0.2456 \cdot 26.7 + 0.0746 \cdot 40.7 \\ & = 34.6. \end{align*} \]

위의 식에서 나타난 비율, 0.6798, 0.2456, 그리고 0.0746의 총합은 1이며, 이들 각각은 가중평균에서 각 국가들에 대한 가중치를 의미한다. 위와 같은 가중평균을 구하는 식은 다음과 같이 축약할 수 있다.

\[\text{weighted average} = \frac{\sum_j N_j \bar y_j}{\sum_j N_j},\]

이때, \(j\)는 국가를 나타내며 가중평균을 구하기 위해서 우리는 각 층위(strata), 여기서는 각 국가 단위에서의 연령의 합을 구해주어야 한다.

Table 3.1: Populations and average ages of countries in North America. (Data from CIA World Factbook 2010.) The average age of all North Americans is a weighted average of the average ages within each country.

Stratum	Label	Population	Average age
1	United States	310 million	36.8
2	Mexico	112 million	26.7
3	Canada	34 million	40.7

3.2 Vectors and matrices

일련의 숫자들의 모임(a list of numbers)을 벡터(vector)라고 한다. 동시에 숫자를 이차원으로 배열한 것(a rectangular array of numbers)은 행렬(matrix)라고 한다. Section 1.2에서 선거 직전 해의 경제적 조건에 따른 미국 대선의 집권당 투표율 예측 예시를 떠올려보자.

\[ \begin{align*} \text{predicted vote percentage} & = 46.3 + 3.0 \cdot (\text{growth rate of average personal income}) \\ \hat y & = 46.3 + 3.0 x \\ \hat y & = \hat a + \hat b x, \end{align*} \]

이때 \(\hat a\)와 \(\hat b\)는 데이터로부터 적합하여 추정해낸 추정값(estimates)을 의미하며, \(\hat y\)는 예측값(predicted value)을 보여준다.

• 위의 예제에서 \(y\)는 실제 선거 결과를 의미한다.

• \(\hat y\)는 모델의 예측 결과를 나타낸다.

이제 이 모델을 몇 가지 특수한 사례들에 적용해보자.

1. \(x = -1\). 경제성장률이 -1%일 때, 모델에 따르면 집권당의 득표율은 \(46.3 + 3.0 * (-1) = 43.3%\)가 된다.

2. \(x = 0\). 경제성장률이 0%, 즉 전혀 성장하지 않았을 때에는 \(46.3 + 3.0 * 0 = 43.3%\)가 된다.

3. \(x = 3\), 약 3%의 경제성장률은 집권당 후보가 이길 수 있는 \(46.3 + 3.0 * 3 = 55.3%\)의 득표율로 이어질 것이다.

Table 3.2: Special cases for the model

a_hat	b_hat	x	formula	y_hat
46.3	3	-1	46.3 + 3 * -1	43.3
46.3	3	0	46.3 + 3 * 0	46.3
46.3	3	3	46.3 + 3 * 3	55.3

위의 적용은 벡터로도 나타낼 수 있다.

\[\hat y = \begin{bmatrix} 43.4 \\ 46.3 \\ 55.3 \end{bmatrix} = \begin{bmatrix} 46.3 + 3.0 \cdot (-1)\\ 46.3 + 3.0 \cdot 0 \\ 46.3 + 3.0 \cdot 3\end{bmatrix},\]

마찬가지로 행렬로도 나타낼 수 있다.

\[\hat y = \begin{bmatrix} 43.4 \\ 46.3 \\ 55.3 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ 1 & 0 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 46.3 \\ 3.0 \end{bmatrix},\]

혹은 더 축약하여 다음과 같이 나타낼 수 있다.

\[\hat y = X \hat \beta,\]

이때 \(y\)와 \(x\)는 길이가 3인 벡터가 된다.⁴ 이때, \(X\)는 \(3\times 2\)의 행렬이 되며, 1 세개는 각각의 \(x\) 사례에서 모델에 포함될 절편을, 그리고 다른 하나의 열은 세 \(x\) 값을 가지게 된다. \(\hat \beta = (46.3, 3.0)\)은 추정된 계수값의 벡터이다. 즉, \(\hat y = X \hat \beta,\)은 일종의 회귀모델의 개념으로 \(\text{예측값} = \text{주어진 관측값}\times\text{모델로 추정한 계수값}\)으로 구성된다고 이해할 수 있다.

3.3 Graphing a line

선형회귀모델을 효과적으로 사용하기 위해서는 회귀모델로 인해 그리는 직선에 대한 대수학(algebra)와 기하학(geometry)적 논리를 이해하는 것이 필요하다.

Figure 3.2는 \(y = a + bx\)에 대한 선을 보여준다.

• 절편(intercept), \(a\)는 \(x\)가 0일 때의 \(y\)의 값이다.

• 계수값(coefficient), \(b\)는 직선의 기울기(slope)를 의미한다.

  • \(b>0\)이면 기울기가 우상향하고 우리는 이 관계를 정의 관계(positive)라고 서술한다.

  • \(b<0\)이면 기울기가 우하향하고 우리는 이 관계를 부의 관계(negative)라고 서술한다.

  • \(b=0\)이면 기울기는 수평해지며, 이때 우리는 \(x\)와 \(y\)의 관계가 독립적이라고 볼 수 있다. 왜냐하면 \(x\)가 어떤 값을 취하던 \(y\)는 항상 일정하기 때문(변하지 않기 때문)에 \(x\)가 \(y\)에 어떠한 영향을 미친다고 볼 수 없기 때문이다.

  • 기울기 값의 절대값이 클수록 그 관계 양상은 심화되며, 기울기는 가팔라진다.

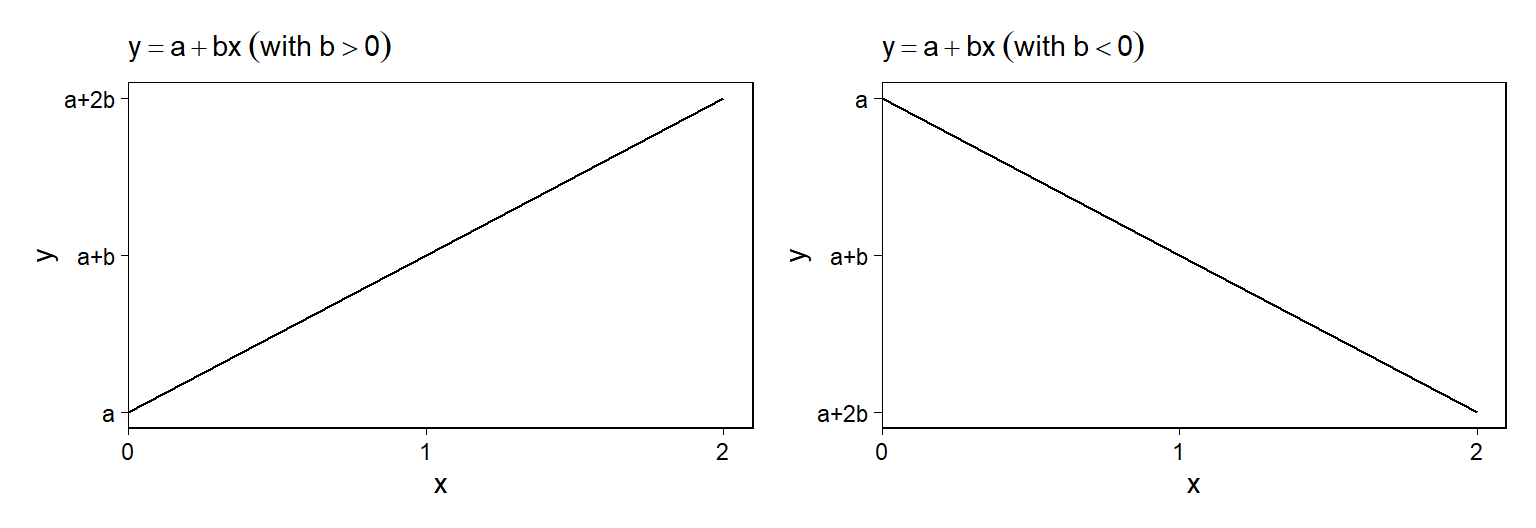
Figure 3.1: Lines y = a + bx with positive and negative slopes.

Figure 3.3a는 \(y = 1007-0.39x\)라는 수리적 예제에 대한 시각화 결과이다. 이 식은 \(x\)가 0일 때 \(y\)는 1007이며, \(y\)는 \(x\)의 한 단위가 증가할 때마다 0.39씩 감소한다는 것을 의미한다. 이 선은 1900년부터 2000년까지 세계 1마일 달리기 애회의 기록과 개략적으로 일치한다(Figure 3.3b).

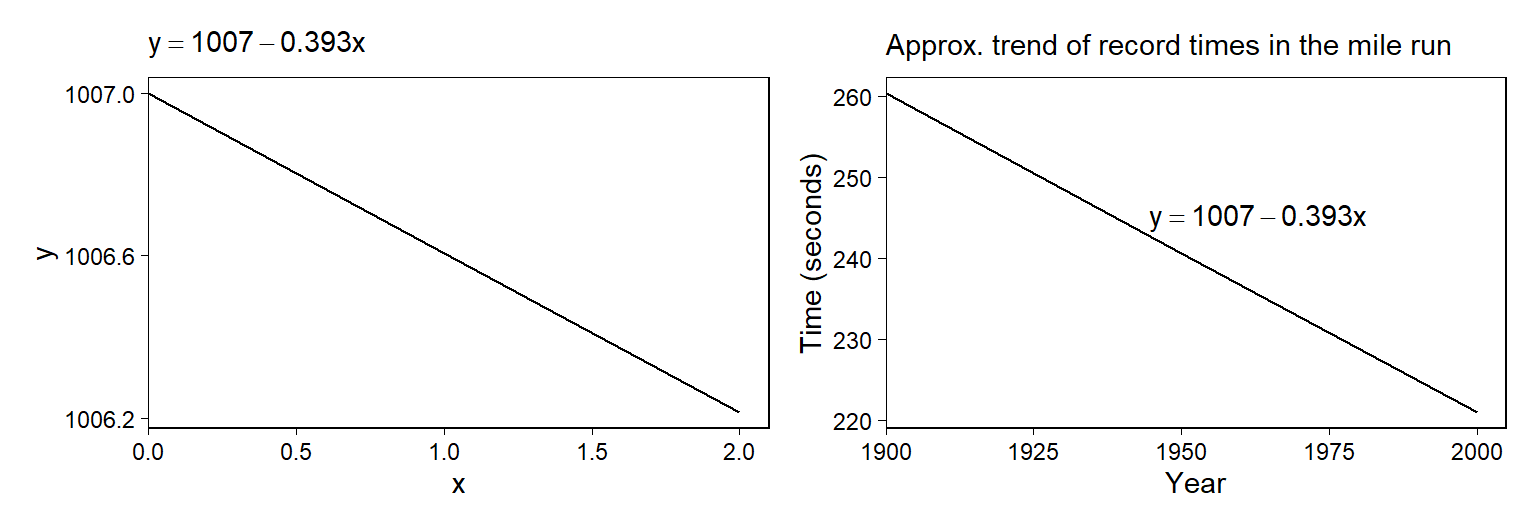
Figure 3.2: (a) The line y = 1007 <U+2212> 0.393x. (b) For x between 1900 and 2000, the line y = 1007 <U+2212> 0.393x approximates the trend of world record times in the mile run. Compare to Figure A.1.

물론 이 결과는 실제 값과는 다르다. 왜냐하면 \(x\)는 현실 세계에서 0일 수 없기 때문이다.

3.4 Exponential and power-law growth and decline; logarithmic and log-log relationships

\(y = a + bx\)의 선은 로그변환(logarithmic transformations)을 통하여 보다 일반적인 관계 양상을 표현하는 데 사용될 수 있다.

\(\log y = a+bx\)는 기하급수적인(exponential) 성장(\(b>0\)일 때)이나 침체(\(b<0\))를 나타내며, \(A = e^a\)라고 할 때, \(y = Ae^{bx}\)로 나타낼 수 있다.

• \(A\)는 \(x= 0\)일때의 \(y\)의 값이다.

• \(b\)는 경제성장률 혹은 침체율의 그 비율(rate)을 결정하는 모수(parameter)이다.

• \(x\)의 한 단위 변화는 \(\log y\)에 있어서의 \(b\)만큼의 추가적인 변화로 이어지며, 이는 곧 \(y\)가 \(e^b\)만큼 변화하는, 일종의 곱셈적 관계로 나타난다. 기하급수적(exponential)이라는 표현을 사용하는 이유는 그 관계가 선형, 직선의 형태로 서술되지 않기 때문이다.

로그 변환이 회귀모델 분석의 해석과 어떠한 관계가 있는지를 나타내기 위해 하나의 예제를 살펴보자. \(y, x\) 모두에 로그변환이 이루어진 상태로 다음과 같은 모델이 존재한다고 하자:

\[ \log y = 1.4 + 0.74\log x. \]

우리는 양변의 로그를 모두 풀어줄 수도 있다. 이때, 위의 식을 변환하지 않은 척도의 \(x\)와 \(y\)로 나타내면 다음과 같다.

\[ \begin{align*} e^{\log y}&=e^{1.4 + 0.74\log x}\\ y&=4.1x^{0.74}. \end{align*} \]

그리고 \(x\)와 \(y\)를 로그변환했을 때는 직선의 형태로 나타났던 관계가, 로그변환을 풀어주면 곡선의 관계로 바뀌게 된다. 당연히 해석하는 방식도 달라질텐데, 여기서 하나의 함의는 원래 비선형 관계인 \(x\)와 \(y\)를 로그변환 등을 통해 직선의 관계로 나타낼 수는 있지만 실질적 해석을 할 때에는 그 둘의 관계가 원래는 비선형이었다는 것을 염두에 두어야 한다는 것이다. 예를 들어, \(\log x\)의 한 단위 증가가 \(\log y\)의 \(\beta\) 만큼의 증가로 이어진다라고 해석하면 누구도 쉽게 이해하지 못할 것이다.

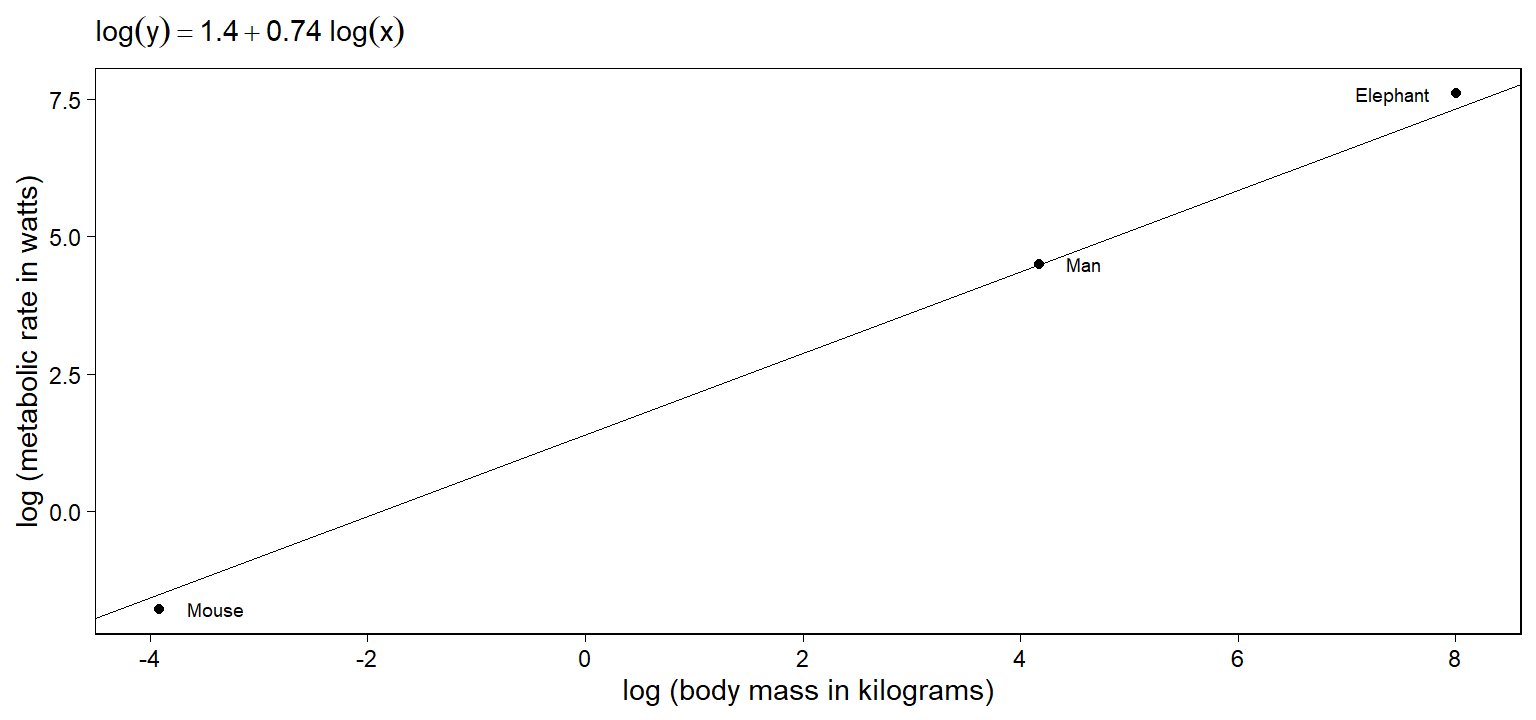
Figure 3.3: Fitted curve of metabolic rate vs. body mass of animals, on the log-log and untransformed scales. The difference from the elephant’s metabolic rate from its predictive value is relatively small on the logarithmic scale but large on the absolute scale.

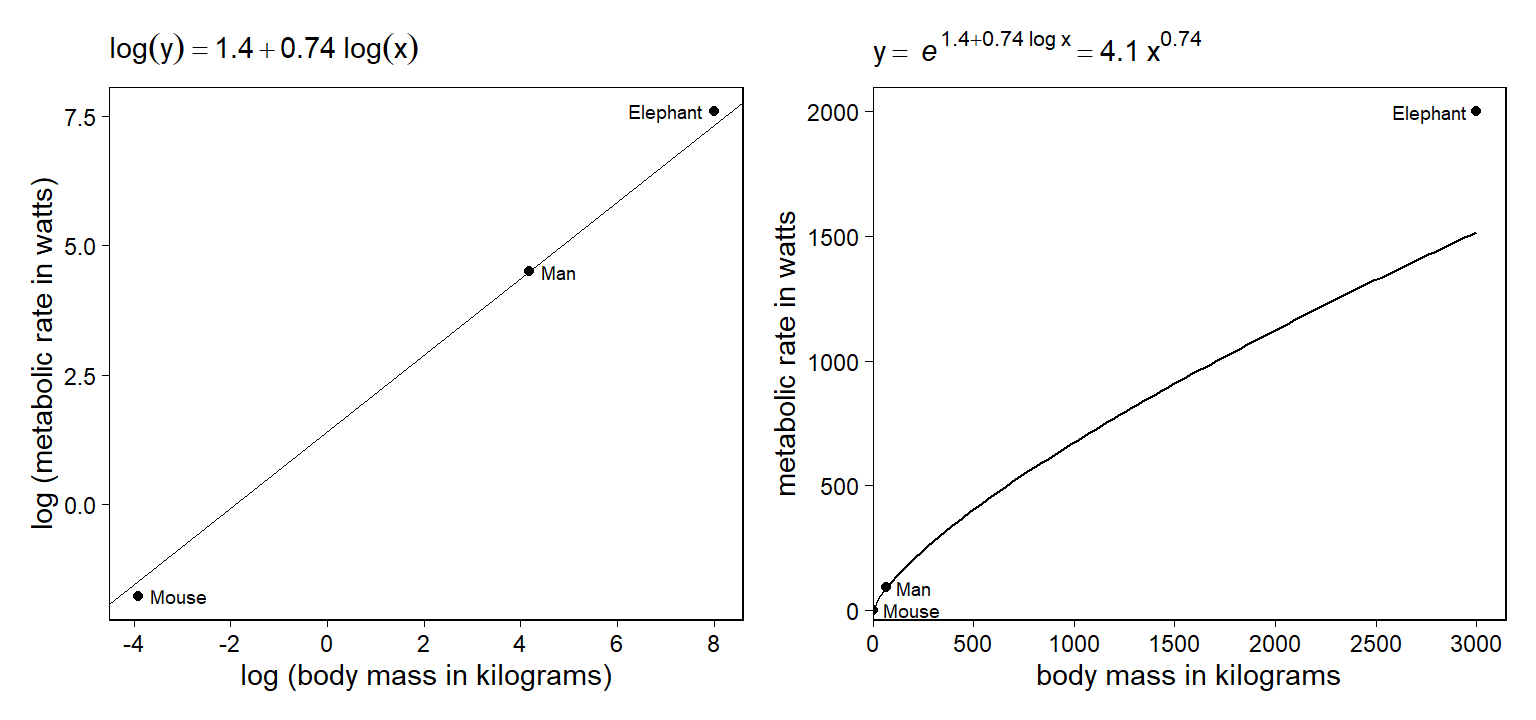
Figure 3.4: Fitted curve of metabolic rate vs. body mass of animals, on the log-log and untransformed scales. The difference from the elephant’s metabolic rate from its predictive value is relatively small on the logarithmic scale but large on the absolute scale.

3.5 Probability distributions

앞에서 기울기와 절편 등은 선형회귀모델의 예측에 있어서의 “결정주의적”(deterministic) 부분을 보여주는 것이었다면⁵, 여기서는 우리의 모델이 정확하게 데이터와 적합하지 않기에 필요한 확률분포와 확률변수라는 개념을 살펴본다.

• 확률분포는 현실 속 모델에 포함되지 않는 측면을 식에서 오차항(error term, \(\epsilon\))으로 나타내며, 위에서 살펴본 모델은 \(y = a + bx + \epsilon\)의 형태로 업데이트 될 수 있다.

• 그리고 이러한 불확실성은 우리가 데이터를 통해 어떠한 인과성 등을 추론하게 하는 원동력이 된다.

우리의 처치⁶는 일종의 개념적 정의와 수리적 공식이 결합된 것이기 때문에 확률분포에 대해 이해는 유용하다. 확률분포에 대한 적용은 다음과 같은 것들을 의미한다.

• \(y_i, i = 1, \dots, n\)으로 나타낼 수 있는 데이터의 분포

• \(\epsilon_i, i = 1, \dots, n\)으로 나타낼 수 있는 오차항의 분포

회귀모델에서 핵심적인 부분은 주어진 예측변수들의 조건 하에서 결과변수들의 값이 어떻게 분포되어 있는지를 살펴보는 것이다.

1. 주어진 예측변수들의 조건 하에서 결과변수의 평균값을 예측한다.

2. 예측값의 변동성(variation)을 요약(summarize)한다.

회귀모델에서 확률분포는 평균을 예측한 이후에 존재하는 분산을 특정하는데 사용된다. 즉, 확률분포란 우리의 예측이 어느 정도의 불확실성을 내포하는지를 추정하고자 하는 모수를 기준으로 보여주는 데 사용된다.⁷

3.5.1 Mean and standard deviation of a probability distribution

확률변수, \(z\)의 확률분포는 일정한 값의 범위를 가진다. 분포의 평균(mean)은 그 모든 범위 값의 평균(average)이다. 평균은 기대값(expected value)라고도 불리며, \(E(z)\) 또는 \(\mu_z\)라고 쓸 수 있다.⁸

한편 확률변수 \(z\)의 분포에 대한 분산(variance)은 \(E((z-\mu_z)^2)\)로 표현할 수 있으며, 각 관측치와 평균 간의 차이를 제곱한 것의 평균값이다.

분포의 변동성 정도에 따라서 \(z\)에 대한 표본추출된 값은 다를 수 있다. 변동성 정도에 따라서 \(\mu_z\)를 기대하였지만 표본의 평균은 그보다 작거나 클수도 있고, 그 차이는 더 커질수도, 작아질수도 있다. 만약 변동성이 존재하지 않는다면, \(z\)의 분산은 0이라고 할 수 있다.

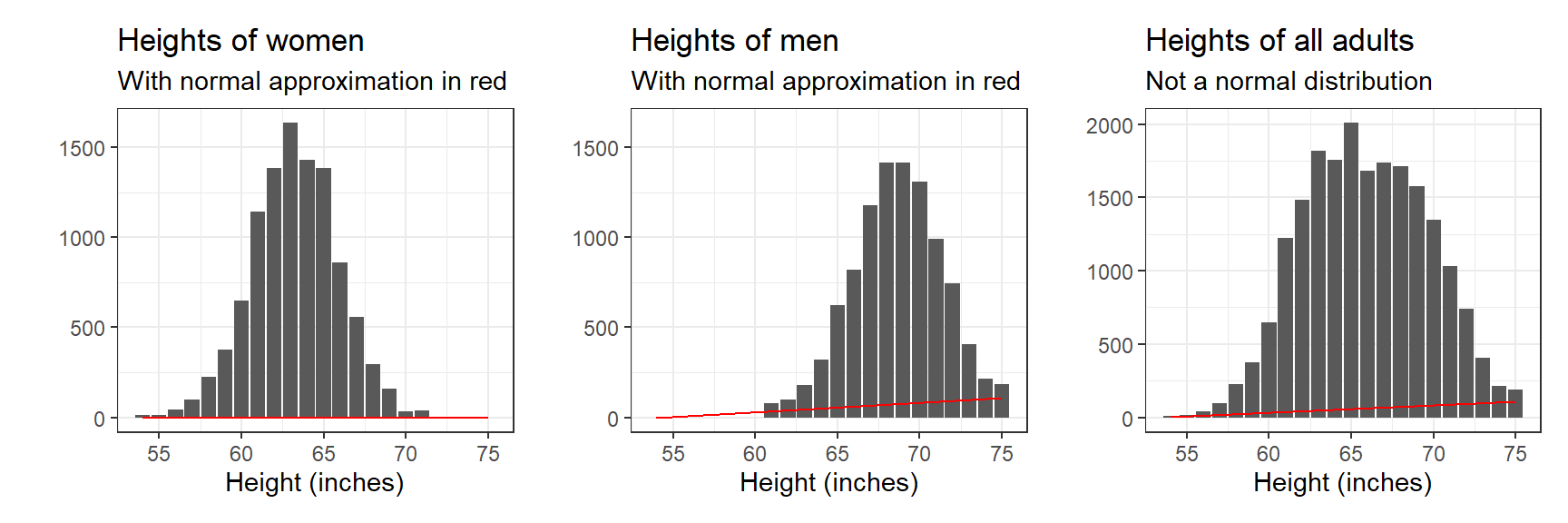
Figure 3.5: (a) Heights of women, which approximately follow a normal distribution, as predicted from the Central Limit Theorem. The distribution has mean 63.7 and standard deviation 2.7, so about 68% of women have heights in the range 63.7 ± 2.7. (b) Heights of men, approximately following a normal distribution with mean 69.1 and standard deviation 2.9. (c) Heights of all adults in the United States, which have the form of a mixture of two normal distributions, one for each sex.

표준편차(standard deviation)는 분산에 제곱근을 취한 것이다. Figure 3.5a에서 여성 키의 표준편차는 2.7인치로, 이는 우리가 모집단에서 무작위로 여성들을 뽑아 표본으로 만들 경우, 그 관측된 값(확률분포), \(z\)에서 평균 키를 빼고 제곱을 취한 뒤 평균을 낸 것에 제곱근을 취한 결과라는 것이다. 즉, \((z-63.7)^2\)을 구한 뒤 평균을 내면 분산이 되고, 그 값이 7.3이라고 할 때, \(\sqrt{7.3} = 2.7\)이 표준편차라고 할 수 있다. 정리하자면 표준편차는 관측치들이 평균적으로 평균으로부터 떨어져 있는 정도를 보여준다고 할 수 있다.

3.5.2 Normal distribution; mean and standard deviation

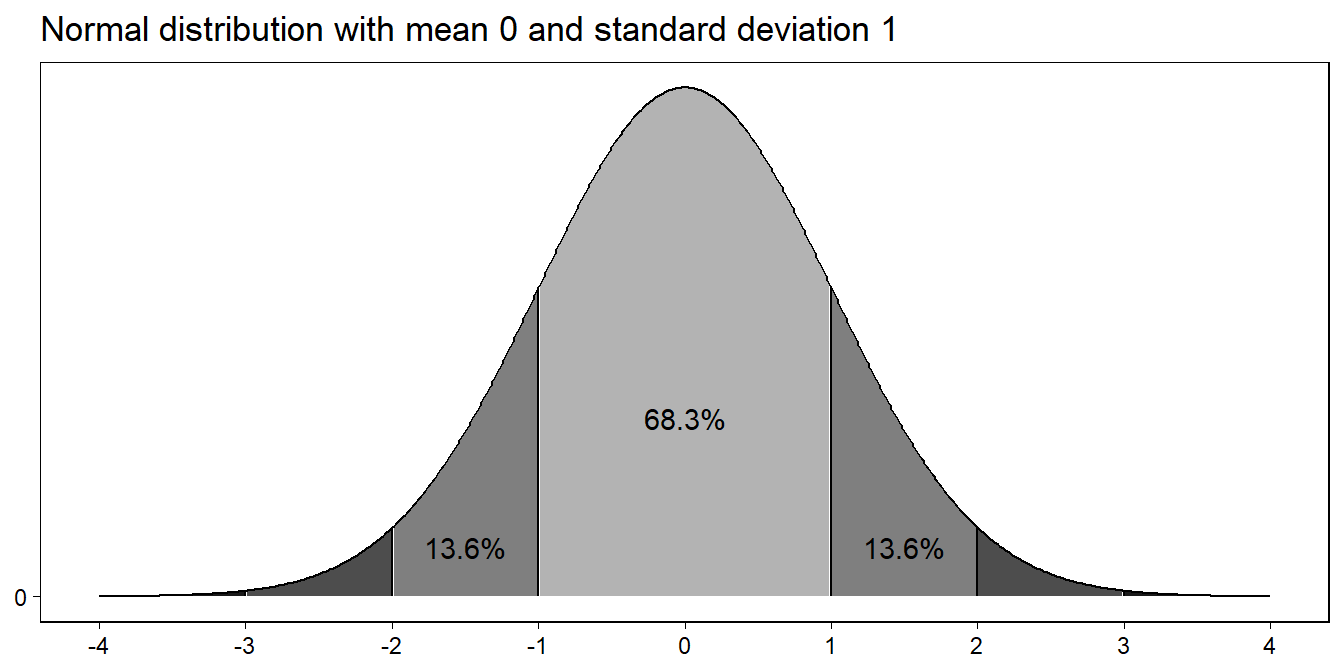
Figure 3.6: Approximately 50% of the mass of the normal distribution falls within 0.67 standard deviations from the mean, 68% of the mass falls within 1 standard deviation from the mean, 95% within 2 standard deviations of the mean, and 99.7% within 3 standard deviations

확률의 중심극한정리(The Central Limit Theorem)는 소규모의 독립적인 확률 변수들의 총합이 정규분포(normal distribution)라 불리는 확률변수로 근사한다는 정리이다.

• 독립적인 각 요소들의 총합: \(z = \sum^n_{i=1}z_i\)

• \(z\)의 평균: \(\mu_z =\sum^n_{i=1}\mu_{z_i}\)

• \(z\)의 분산: \(\sigma_z = \sqrt{\sum^n_{i=1}\sigma^2_{z_i}}\)

• 수리적으로 정규분포는 \(z\sim \mathrm{N}(\mu_z, \sigma^2_z)\)라고 쓸 수 있다. 확률변수 \(z\)는 평균–\(\mu_z\)와 분산–\(\sigma^2_z\)를 가지는 분포라는 의미이다.

• 앞으로 평균 \(\mu\)와 표준편차 \(\sigma\)를 가지는 정규분포를 \(\mathrm{N}(\mu, sigma^2)\)라고 쓴다.

  • 대략적으로 이 분포에 속한 값들의 50%는 \(\mu \pm 0.67\sigma\)에 속하는 값의 범위에 떨어지게 된다.

  • 약 68%에 해당하는 값들은 \(\mu \pm \sigma\)의 범위 내에 속하게 되며, 95%의 값들은 \(\mu \pm 2\sigma\)에, 99.7%의 값들은 \(\mu \pm 3\sigma\)의 범위 내에 위치하게 된다(Figure 3.6 참고).

정규분포는 총합, 차이, 그리고 추정된 회귀계수 등을 평균 또는 가중평균 등의 수리적 표현으로 나타낼 수 있다는 점에서 유용하다.

3.5.3 Linear transformations

정규분포는 선형변환(linear tranformation)해도 여전히 정규성을 지닌다. 만약 \(y\)가 남성의 키를 인치로 나타낸 변수로 그 평균이 69.1이라고 하고 표준편차가 2.9라고 하자. 그러면 2.54 \(y\)는 센티미터로의 키를 의미하며, 평균은 \(2.54*69 = 175\)가 되며 표준편차는 \(2.54*2.9 = 7.4\)가 된다.

3.5.4 Mean and standard deviation of the sum of correlated random variables

평균이 \(\mu_u,\mu_v\)이고 표준편차가 \(\sigma_a, \sigma_b\)인 두 확률변수 \(u\)와 \(v\)가 있다고 하자. 이때, 이 두 변수의 상관관계(correlation)은 \(\rho_{uv} = \mathrm{E}((u-\mu_u)(v-\mu_v))/(\sigma_a\sigma_b)\)로 나타낼 수 있다. 그리고 상관관계는 \([-1, 1]\)의 범위 내에 존재하게 된다.

상관관계는 \(u\)와 \(v\)의 선형결합에 관한 정보를 제시한다. 두 변수의 합(\(u+v\))의 평균은 \(\mu_u + \mu_v\)로, 표준편차는 \(\sqrt{\sigma^2_{u} + \sigma^2_{v} + 2\rho\sigma_u\sigma_v}\)로 나타낼 수 있다. 일반적으로 가중치가 부여된 합(\(au + bv\))는 \(a\mu_u + b\mu_v\)를 평균으로, \(\sqrt{a^2\sigma^2_{u} + b^2\sigma^2_{v} + 2ab\rho\sigma_u\sigma_v}\)를 표준편차로 가진다. 마찬가지로 두 변수의 차이인 \(u-v\)의 평균은 \(\mu_u-\mu_v\)로, 표준편차는 \(\sqrt{\sigma^2_{u} + \sigma^2_{v} - 2\rho\sigma_u\sigma_v}\)이다.

3.5.5 Lognormal distribution

로그변환은 0이나 음수값을 취하는 것을 허용하지 않기 때문에 로그 척도로 확률변수를 변환할 경우 모두 양수값을 가지게 된다. Figure 3.7은 미국 내 남성들의 로그를 취한 몸무게와 몸무게의 원변수의 분포를 각기 보여준다.

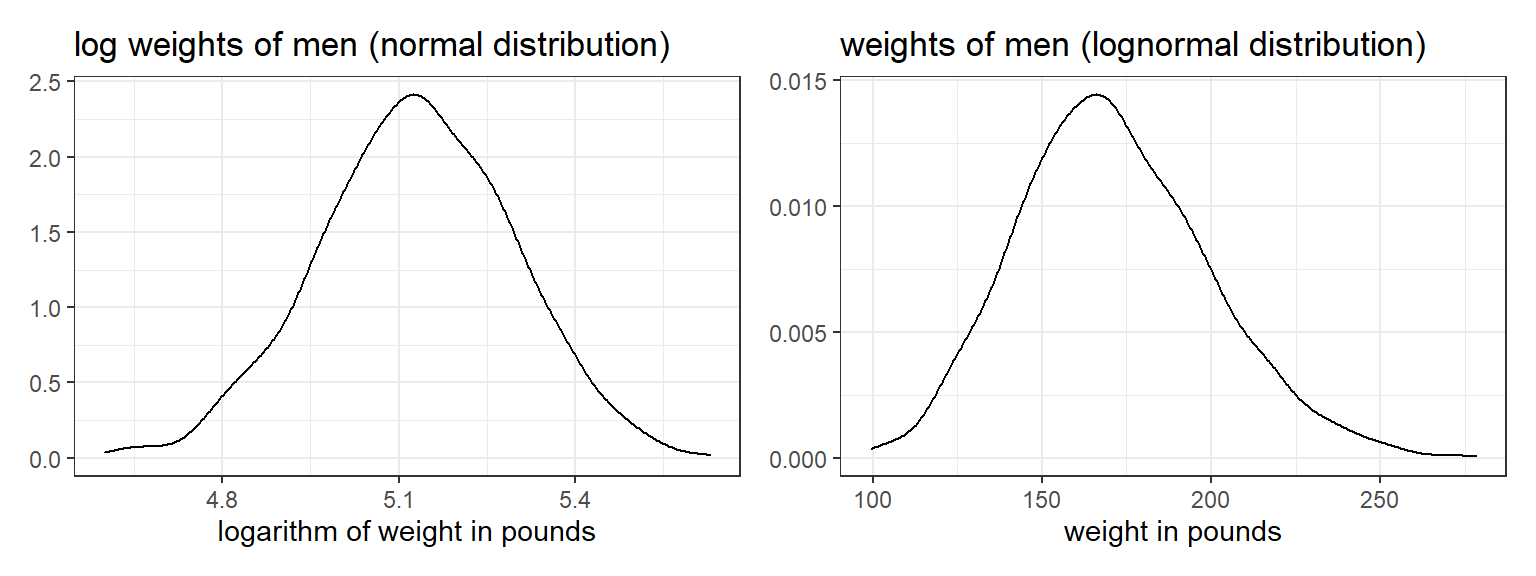
Figure 3.7: Weights of men (which approximately follow a lognormal distribution, as predicted from the Central Limit Theorem from combining many small multiplicative factors), plotted on the logarithmic and original scales.

3.5.6 Binomial distribution

농구에서 20발의 슛을 쐈다고 하고, 성공률이 0.3이며 각각의 슈팅은 서로 독립적이라고 가정하자. 그러면 우리는 \(n=20\)에 \(p=0.3\)인 이항분포(binomial distribution)이며, \(y\sim \mathrm{binomial(n, p)}\)로 나타낼 수 있다. \(n\), \(p\)의 모수를 갖는 이항분포는 \(np\)를 평균으로, \(\sqrt{np(1-p)}\)를 표준편차로 갖는다.

3.5.7 Poisson distribution

포아송 분포는 암발병 환자의 수나 웹사이트 방문자 수와 같은 횟수와 관련된 카운트 데이터에 사용되는 분포이다. 정치학 분야에서는 전쟁 횟수 등과 같은 종속변수를 분석하기 위해 사용될 수 있다.

3.5.8 Unclassified probability distribution

실제 데이터가 항상 특정한 확률 분포와 대응되는 것은 아니다. 하지만 확률분포의 종류는 실제 데이터를 이해 및 분석하는 데 있어서 일종의 가이드라인을 제시한다.

3.5.9 Probability distributions for error

회귀모델은 실제 데이터의 변동성으로 수립할 수 있는 "결정적 모델(deterministic model)"과 오차(error), 또는 설명되지 않는 변동성을 포착하기 위해 포함되는 확률분포로 이루어진다.

3.5.10 Comparing distributions

평균과 같은 요약치들을 이용해 분포들을 비교하기도 하지만 분위(quantiles)의 변화 등도 살펴볼 필요가 있다. 평균은 집단의 중심경향성(central tendancy)을 보여주는 값이기는 하지만, 분포가 치우쳐 있을 경우(skewed), 평균이 대표값으로 유용하지 않을 수도 있고, 평균 그 자체는 불확실성 정도를 보여주지 못하기 때문이다.

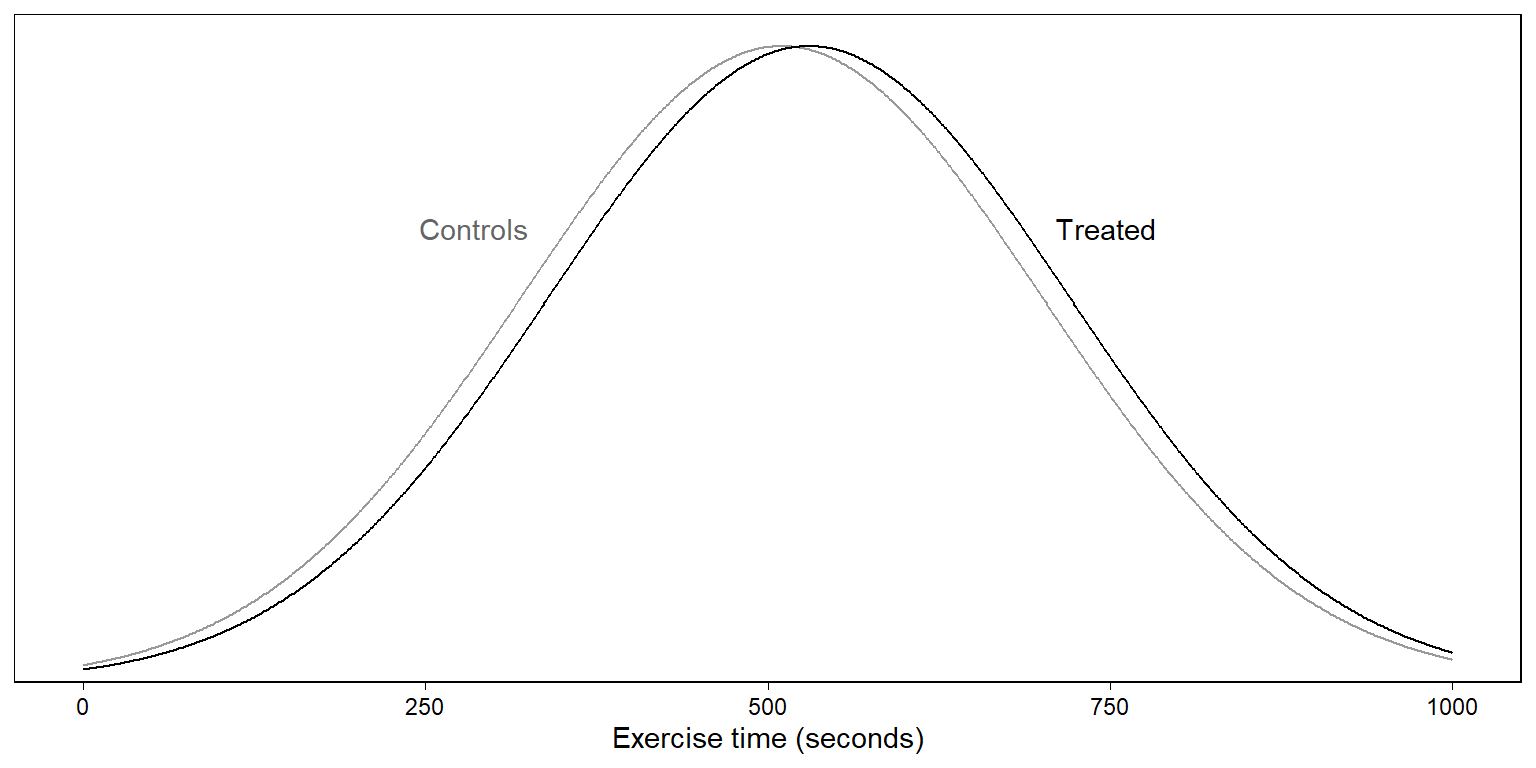
Figure 3.8: Distributions of potential outcomes for patients given placebo or heart stents, using a normal approximation and assuming a treatment effect in which stents improve exercise time by 20 seconds, a shift which corresponds to taking a patient from the 50th to the 54th percentile of the distribution under the placebo.

3.6 Probability modeling

두 명의 후보와 \(n\)명의 유권자가 참여하는 선거가 있다고 가정하자. 만약 모든 유권자가 정확히 반반으로 갈라지거나 (\(n\)이 짝수일 때), 후보가 득표한 수가 서로 동수일 때 (\(n\)이 홀수 일 때), 한 표 한 표가 더해질 때마다, 그 표들은 잠재적으로 결과를 “결정지을 수 있는” 표가 된다(승부를 결정하는 표).

이 경우, 확률을 추정하기 위해 두 가지 방법을 생각해볼 수 있다: 첫째는 경험적으로 예측하는(forecasting) 접근법이고, 둘째는 이항확률모델을 사용하는 것인데, 이 경우는 심각한 문제를 가지고 있다.

3.6.1 Using an empirical forecast

\(y\)가 후보 중 한 명이 받을 표의 비율이라고 하고, \(y\)의 불확실성은 평균 0.49, 표준편차 0.04의 정규분포로 나타낼 수 있다고 하자. 즉, 후보자가 질 거라고 예측되지만(평균이 \(0.49 < 0.5\)), 불확실성을 감안하면 실제 결과는 이길수도, 질수도 있다는 것이 된다(\(0.49-0.04 < 0.05 < 0.53\)). \(n\)명의 표가 \(n\)이 짝수일 때 정확하게 갈라질 확률 또는 \(n\)이 홀수일 때 딱 한 표 차이로 나뉘게 될 확률은 \(1/n\)에 0.5의 예측 득표율 밀도의 곱으로 나타낼 수 있다.

• 예를 들어, 200,000명의 유권자가 있는 선거에서 이 확률은 아래와 같이 계산할 수 있다.

  dnorm(0.5, 0.49, 0.04)/2e5

  ## [1] 4.833351e-05

• 결과는 약 4.8e-5로 약 \(1/21000\)에 근사하는 값이다.

이 값은 개별 유권자에게 있어서는 매우 낮은 확률이지만 캠페인에 있어서는 그다지 낮다고 보기는 힘들다. 유권자 수가 늘어날수록 이 확률은 점차 증가할 것이기 때문이다.

3.6.2 Using an reasonable-seeming but inappropriate probability model

\(n\)명의 유권자가 있고, 특정 후보에게 투표할 확률이 \(p\)라고 하자. 둘이 정확하게 동점이 되거나 혹은 동점에서 딱 한 표가 모자랄 확률은 이항분포를 통해서 계산할 수 있다. 예를 들어, \(n=200,000\)이고 \(p=0.5\)라고 할 때, 선거 동수의 확률은 다음과 같이 계산할 수 있다.

dbinom(1e5, 2e5, 0.5)

## [1] 0.001784122

그런데 이항분포 모델을 사용했을 때의 문제가 무엇일까? 가장 직접적으로 이항분포 모델을 사용할 수 없는 이유는 그 분포가 \(n\)번의 독립시행에서의 \(p\)의 확률에 따른 성공의 횟수를 나타낸다는 것에 있다. 하지만 유권자들은 독립적으로 의사결정을 내리지 않는다. 그들의 결정은 홍보, 후보자들의 연설, 뉴스 등과 같은 여러 공통적 요인들에 의해 영향을 받는다. 게다가 유권자들은 확률 \(p\)를 공유하지도 않는다. 유권자들의 당파성은 서로 독립적이지도, 동일하지도 않다.

어기서의 선거 예제에서 핵심적인 문제점은 이항 모델이 불확실성을 잡아내는 데 썩 훌륭하지 않다는 것이다. \(n\)명의 유권자가 독립적인 의사결정을 한다고 하고, 비현실적이지만 각각이 특정 후보에게 투표할 확률 \(p\)를 동일하게 갖는다고 가정하자. 만약 \(p\)가 유권자 전체의 평균 확률로 해석될 수 있다면, 이 \(p\) 자체는 어디서 오는 걸까? 실제 선거에서 우리는 이 확률을 결코 알 수 없다. 즉, 어디까지나 가정해야하기 때문에 불확실성을 포착할 수 없는 것이다.

3.6.3 General lessons for probability modeling

결과적으로 우리는 확률모델을 경험적 함의(emplical implications)로 확인할 필요가 있다. 만약 확률모델이 상식적으로 말이 안되는 예측을 내놓는다면, 모델에 무언가 문제가 있는지를 확인할 기회를 가지게 되고, 어떠한 가정이 위배되는지를 검토할 수 있게 된다.

확률모델에 문제가 있을 경우에, 우리는 그 (예측)실패를 우리의 이해를 제고하기 위한 방법으로 사용할 수 있기 때문에, 예측모델은 강력한 분석도구라고 할 수 있다.

---

4. 위에서 \(x\)에 해당하는 경제성장률도 세 개의 값을 줬기 때문에 그에 따라서 예측되는 \(\hat y\)도 세개가 되므로, 각각은 길이가 3인 벡터가 된다.↩︎

5. 여기서 결정주의적이라는 의미는, 확실한 혹은 무작위가 아니(비체계적이지 않은)라는 의미로 이해할 수 있다.↩︎

6. GHV는 처치라는 표현을 많이 쓰는데, 풀어서 이해하자면 우리가 종속변수, 혹은 결과변수인 \(y\)에 주요한 영향을 미칠 것으로 기대하는 예측변수, 설명변수라고 이해할 수 있다. 예컨대, 통계에서 \(x_1\)이 우리가 기대하는 주요 예측변수고 \(x_2\cdots x_n\)이 선행연구 등을 통해 종속변수에 영향을 미칠 수 있는 여타의 변수로서 모델에 포함된 통제변수라고 할 때, 우리는 \(x_1\)의 값이 변화할 때(처치가 가해질 때)의 $ y$의 변화를 통해서 \(x_1\)과 \(y\)의 관계를 추론하고자 하는 것이다.↩︎

7. \(\alpha\)라고 하는 모집단의 모수(parameter)를 추정하기 위해 표본을 통해 \(a\)라는 통계치(statistics)를 얻었다고 하자. 우리는 모집단과 표본 간에 존재하는 필연적 불확실성–표본이 아무리 모집단을 대표한다고 해도 표집방법 등과 같은 이유로 나타날 수 밖에 없는 오차로 인해여 통계치가 완벽하게 모수와 동일하다고 확신할 수 없다. 즉, 통계치는 일정한 불확실성을 수반하게 되는데, 확률분포는 이 불확실성을 보여주기 위해 사용된다.↩︎

8. 하지만 이 부분은 조금 더 부연설명이 필요한데, 모집단을 대표하는 값을 기대값이라고 할 때, 현실적으로 우리가 가진 데이터(표본)을 대표할 수 있는 값 중 하나가 평균이다. 그래서 평균을 표본 수준에서 일종의 기대값에 대응하는 개념으로 사용하는 것이지 엄밀하게 말하면 평균 = 기대값이라고 보기에는 무리가 있다.↩︎