Chapter 4 Statistical Inference

통계적 추론은 데이터에 기초하여 모집단의 모수에 관한 예측을 추정과 불확실성을 포함한 진술의 형태로 구성하는 것이다. 즉, 데이터가 현실 속에서 우리가 연구하고자 하는 모집단에 대한 하나의 표본이라고 할 때, 그 표본을 통해 모집단에서 존재하는 관계양상 등(모수)에 관해 예측하고, 그 예측에는 표본-모집단의 관계로 인한 불확실성이 존재하기에 그것 또한 반영하여 진술(statement)의 형태로 가공해내는 것이다.

이 챕터에서는 확률모델, 추정(estimation), 편향(bias), 분산, 그리고 통계적 추론의 해석과 통계적 오차에 관한 기본적인 내용들을 다룬다. 나아가 통계적 추론에서 불확실성의 개념이 어떻게 연계되는지를 살펴보고 잡음이 있는 데이터(불확실성을 포함한 데이터)로부터 확실성을 이끌어내기 위해 가설 검정과 통계적 유의성을 사용하는 것의 문제 또한 짚어본다.

4.1 Sampling distributions and generative models

4.1.1 Sampling, measurement error, and model error

우리는 불완전하거나 혹은 미비한 데이터를 바탕으로 통계적 추론을 이끌어낸다. 추론의 역할은 다음과 같다.

• 표집모델(sampling model): 우리가 알고 싶은 것은 모집단에 대한 특성이지만 모집단을 직접 관측하거나 확보할 수 없기때문에 우리는 모집단으로부터 추출한 표본으로부터 모집단의 특성을 추정해야만 한다.

• 측정오차모델(measurement error model): 우리는 기저의 어떠한 패턴이나 법칙(law)에 대해 알고싶지만 현실에서 측정된 데이터는 항상 오차를 수반한다. 측정오차가 항상 예측변수들과 독립적인 것(혹은 가산형, additive)은 아니다⁹: 때로는 승산형(multiplicative) 모델이 더 말이 될 수 있고, 이산형 데이터를 모델링할 때는 이산형 분포가 필요할 수도 있다.

• 모델오차(model error): 실제 데이터에 적용하는데 있어서 모델이 가지는 본연적 불완전성을 의미한다.

위의 세 통계적 추론에 대한 패러다임은 서로 다른 특징을 가진다. 예를 들어, 표집모델은 측정에 관해서는 구체적으로 설명하지 않고, 완벽한 데이터가 관측되더라도 측정오차모델에 대한 접근법을 취할 수 있다. 그리고 모델 오차는 완벽하게 정확한 관측치들을 대상으로도 제기될 수 있는 문제이다. 통계모델을 수립하고, 통계모델을 가지고 작업하는 과정에서 위의 세 문제 모두 고려해야 한다.

Gelman, Hill, and Vehtari (2020) 은 측정오차모델(\(y_i = a + bx_i + \epsilon_i\))의 분석틀에서 회귀모델을 수립하는 접근법을 취하고 있다. 이때, \(\epsilon_i\)은 모델 오차로 해석할 수 있으며, 동시에 표본과 모집단의 관계에서는 가설적인 초모집단(superpopulation)이라고 할 수 있는 분포로부터 무작위로 표본을 추출하며 나타난 일련의 표집오차들(sampling errors), \(\epsilon_1,\dots,\epsilon_n\)로 볼 수도 있다.

4.1.2 The sampling distribution

표집분포는 데이터 수집 과정이 반복될 때, 관측될 수 있는 일련의 “가능한(possible)” 데이터셋을 의미한다. 우리가 관심을 가지고 연구하고자 하는 모집단이 존재한다고 할 때, 확률적으로 표본을 추출할 경우, 우리는 여러 표본들을 얻을 수 있을 것이다. 그리고 그 표본들의 분포를 표집분포라고 한다.

하지만 우리는 실제로 표집분포를 알 수는 없고 단지 추정할수만 있을 뿐이다. 왜냐하면 모집단을 모르기 때문에 모집단에서 표본들이 어떻게 추출되었는지 알 수 없다는 것이다. 마찬가지로 측정오차모델에서 표집분포는 데이터로부터 추정된 알려지지 않은 모수 \(a\), \(b\), 그리고 \(\sigma\)에 좌우된다.

데이터가 무작위(확률적) 과정을 통해 수집되지 않았다면, 통계적 추론을 위해서는 데이터에 관한 어떤 확률모델을 가정하는 것이 유용하다. 표집분포는 생성모델(generative model)이라고도 불린다.¹⁰

4.2 Estimates, standard errors, and confidence intervals

4.2.1 Parameters, estimands, and estimates

모수(parameters)는 통계모델을 결정하는 “알려지지 않은 수,” 모집단의 특성을 의미한다. 예를 들어, 아래와 같은 모델이 있다고 하자.

\[ y_i = a + bx_i + \epsilon_i, \: \epsilon \sim \mathrm{N}(0, \sigma). \]

• 계수(coefficients): \(a\)와 \(b\)

• 분산(variance): \(\sigma\)

한편 추정치(estimand) 또는 우리가 관심을 갖는 통계치(quantity of interests)는 추정하고자 하는 데이터 또는 모수에 대한 요약을 제공한다. 위의 모델에서는 \(a\), \(b\), 즉 절편과 계수가 우리가 관심을 가진 추정치라고 할 수 있으며, 또는 모델을 통해 산출안 예측값(predicted values)이 우리가 관심을 갖는 추정치일 수도 있다.

4.2.2 Standard errors, inferential uncertainty, and confidence intervals

표준오차(standard error)는 추정된 값에 대한 “추정된(estimated)” 표준편차를 의미하며, 우리가 관심을 갖는 추정량의 불확실성 정도를 보여주는 지표이다.

• 표준오차는 추정치의 변동성을 보여주는 측정지표이면서 표본의 규모가 더 커질수록 표준오차는 감소하고 종래에는 거의 0에 수렴하게 된다.

신뢰구간(confidence interval)은 주어진 표집분포의 가정 하에서 데이터와 대략 일치하는 모수 또는 추정하고자 하는 통계치의 값의 범위를 나타낸다. 간단히 얘기하자면, 모집단의 평균이라는 모수를 추정하고자 할 때, 우리는 표본을 통해 어떠한 값의 범위 안에 그 모수가 존재할 것이라고 기대하는 신뢰구간을 표본을 통해 산출할 수 있다.

대개 대규모 표본을 대상으로 표집분포가 정규분포를 따른다는 가정 하에 추정치로부터 \(\pm2\) 표준오차의 범위의 95% 신뢰구간을 추정한다.

4.2.3 Standard errors and confidence intervals for average and proportions

표본규모가 \(n\)인 단순무작위 추출된 표본으로 무한대의 값을 가지는 모집단의 평균을 추정할 때, 그 표준오차는 \(\sigma\sqrt{n}\)이며, 이때 \(\sigma\)는 모집단의 측정지표에 대한 표준편차가 된다.

한편, 데이터가 연속형이 아니라 이산형, 특히 0과 1을 값으로 가질 경우에는 평균(average)은 데이터에서 1이 갖는 비율(proportion)과 같다. 예를 들어, \(n\)명의 응답자를 상대로 설문을 하고 예(Yes)라고 말한 사람의 수를 \(y\), 무응답자의 수가 \(n-y\)라고 하자. 이 경우에 설문을 통해 모집단에서 예라고 응답한 사람의 비율(\(\hat p\))을 추정하면, \(\hat p = y/n\)이 된다. 그리고 이때 표준편차는 \(\sqrt{\hat p (1-\hat p)/n}\)이 된다.

• 만약 모집단에서의 응답비율, \(p\)가 거의 \(0.5\)라고 한다면, 표본에서의 비율은 표본크기에 따라서 달라질 수 있으며, 대략 \(0.5/\sqrt n\)로 근사한다고 할 수 있다.

• 만약 표본에서의 응답비율이 \(0.5\)라면 \(\sqrt{0.5*0.5} = 0.5\), \(0.4\)라면 모수에 대한 추정치는 \(\sqrt{0.4*0.6}=0.49\), \(0.3\)이라면 \(\sqrt{0.3*0.7}=0.46\)가 된다.

• 비율에 대한 신뢰구간을 표준오차 공식에 따라서 계산해보자. 1000명의 무작위 표본 중 700명이 사형제 지지, 300명이 사형제 반대한다고 할 때, 모집단에서의 지지자 비율에 대한 95% 구간은 \([0.7\pm2\sqrt{0.7*0.3/1000}] = [0.67, 0.73]\)로 도출된다. 이 구간은 모수, \(0.7 (700/1000)\)을 포함한다. R로도 계산해볼 수 있다.

4.2.4 Standard error and confidence interval for a proportion when \(y = 0\) or \(y = n\)

\(y=0\)이거나 \(n-y = 0\)인 극단적인 경우, 표준오차의 추정값은 0이되며, 신뢰구간의 너비도 0이 된다.

n <- 1000
y <- 0
estimate <- y/n
se <- sqrt(estimate*(1-estimate)/n)
int_95 <- estimate + qnorm(c(0.025, 0.975)) * se
int_95

## [1] 0 0

4.2.5 Standard error for a comparison

두 독립적인 값의 차이에 대한 표준오차는 다음과 같이 계산할 수 있다.

\[ \text{standard error of the difference} = \sqrt{se^2_1 + se^2_2}. \]

예를 들어, 1000명을 대상으로 한 설문에서 400명은 남성, 600명은 여성이었다고 해보자. 이들에게 다음 선거 때 누구에게 투표할 생각이 있느냐고 물었을 때, 남성 중 57%, 여성 중 45%가 공화당 후보에게 투표할 것이라고 응답했다고 하자. 이때 남성의 공화당 후보에 투표할 비율에 대한 표준오차는 \(\text{se}_\text{men} = \sqrt{0.57*0.43/400}\), 여성의 경우는 \(\text{se}_\text{women} = \sqrt{0.45*0.55/600}\)으로 계산할 수 있다. 따라서 추정된 공화당 지지에 대한 성별의 차이는 \(0.57-0.45 = 0.12\)이며, 그 표준오차는 \(\sqrt{\text{se}_\text{men}^2 + \text{se}_\text{women}^2} = 0.032\)라고 할 수 있다.

4.2.6 Sampling distribution of the sample mean and standard deviation; normal and \(\chi^2\) distributions

평균이 \(\mu\)이고 표준편차가 \(\sigma\)인 정규분포로부터 \(n\)개의 관측치(\(y_1,\dots y_n\))를 추출했을 때, 표본의 평균은 \(\bar{y} = \frac{1}{n}\sum^{n}_{i=1}y_i\)가 되고, 표준편차는 \(s_y = \sqrt{\frac{1}{n-1}\sum^n_{i=1}(y_i-\bar{y})^2}\)라고 할 수 있다. 이때, 표본평균과 표본표준편차는 정규분포에서 독립적인 표본들을 무작위추출했다는 가정 하에서 일종의 표집분포를 이룰 수 있다. 예를 들어, 모집단으로부터 무수히 많은 표본들을 뽑아 그들 각각의 평균을 구한다면, 그 평균이 또 하나의 분포를 이룰 수 있다는 것이다. 그리고 표본 추출 횟수가 증가할수록(\(n\uparrow\)), 그 표본평균은 정규성을 띄게 될 것이다. 따라서 우리는 표본평균 \(\bar{y}\)가 모집단 평균 \(\mu\)를 중심으로 추출횟수, 표본규모에 따른 표준편차 \(\sigma/\sqrt{n}\)를 가지는 정규분포를 가지게 될 것이라고 기대할 수 있다. 마찬가지로 표본의 표준편차는 \(s^2_y*(n-1)/\sigma^2\)로, \(n-1\)의 자유도(degree of freedom)를 가지는 \(\chi^2\)(카이스퀘어) 분포를 띄게 된다.

4.2.7 Degrees of freedom

그렇다면 대체 자유도란 무엇일까? Gelman, Hill, and Vehtari (2020) 은 “적합된 모델로부터 예측값들의 오차를 추정할 때, 과적합(overfitting)의 문제를 교정할 필요가 있다”라는 말로 자유도의 개념을 설명하는데, 조금 알아듣기 어렵다. 간단히 정리하면, 자유도란 주어진 조건 하에서 통계적 제한을 받지 않고 자유롭게 변화를 줄 수 있는 관측치의 수를 의미한다. 예를 들어, \(x + y + z = 12\)라는 수식이 있다고 할 때, 자유도는 몇 개일까? 일견 미지수가 3개이므로 자유도가 3이라고 생각할 것 같지만 여기서의 자유도는 2이다. 왜냐하면 \(x\)와 \(y\)의 값이 결정되는 순간, \(z\)의 값은 자유롭지 못하고 고정되기 때문이다.

• 자유도가 작을수록 과적합을 조정해주어야할 필요성은 증가한다. 왜냐하면 변수가 자유롭지 않다는 얘기는 딱 그 표본에 한하여 모델이 유효할 가능성이 높다는, 즉 일반화하기 어렵다는 문제를 해결해야 한다는 의미이기 때문이다.

• 자유도의 문제는 모델에서의 잔차의 추정에 있어서의 불확실성과 연관되는데, 자세한 내용은 11장에서 살펴보도록 한다.

4.2.8 Confidence intervals from the \(t\) distribution

\(t\) 분포는 정규분포와 비슷하지만 양 끝 꼬리가 조금 더 두터운 분포를 말한다. 관측치의 개수가 많아지면 (자유도가 커질수록) \(t\) 분포는 정규분포에 수렴하게 된다.

만약 표준오차가 \(n\)개의 데이터로 추정된다면, 우리는 \(n-1\)의 자유도를 가진 \(t\) 분포를 이용해 그 불확실성을 설명할 수 있다. 정규분포와 \(t\) 분포의 차이는 자유도의 크기 차이라고 봐도 무방하다.

y <- c(35, 34, 38, 35, 37)
n <- length(y)
estimate <- mean(y)
se <- sd(y)/sqrt(n)
int_50 <- estimate + qt(c(0.25, 0.75), n-1)*se
int_95 <- estimate + qt(c(0.025, 0.975), n-1)*se
int_50;int_95

## [1] 35.2557 36.3443

## [1] 33.75974 37.84026

4.2.9 Inference for discrete data

이항변수가 아닌 이산형 데이터에 대해서도 연속형 변수의 표준오차를 계산하는 공식을 적용할 수 있다. 1000명의 무작위 표집된 성인을 대상으로 그들이 개를 몇 마리 소유하였는지를 설문하였다고 하자. 600명은 개가 없다고 응답했고, 300명은 1마리를, 50명은 2마리를, 30명이 3마리를, 20명이 4마리의 개가 있다고 응답했다. 이때, 모집단에서 소유한 개의 평균 수에 대한 95% 신뢰구간은 어떻게 추정할 수 있을까?

N	Mean	Standard Deviation	Standard Error	C.I. (Low)	C.I. (High)
1000	0.57	0.875	0.028	0.516	0.624

4.2.10 Linear transformations

선형변환된 모수에 대한 신뢰구간을 구하기 위해서는 그 구간도 선형변환의 형태를 취한다. 예를 들어, 일인당 소유한 개의 평균의 신뢰구간이 \([0.52, 0.62]\)라고 할 때, 백만명을 대상으로 하면 그 구간은 \([520,000, 620,000]\)이 되는 셈이다.

4.2.11 Comparisons, visual and numerical

Figure 4.2는 표본 별 불확실성을 시각적으로 비교할 수 있도록 만든 플롯이다.

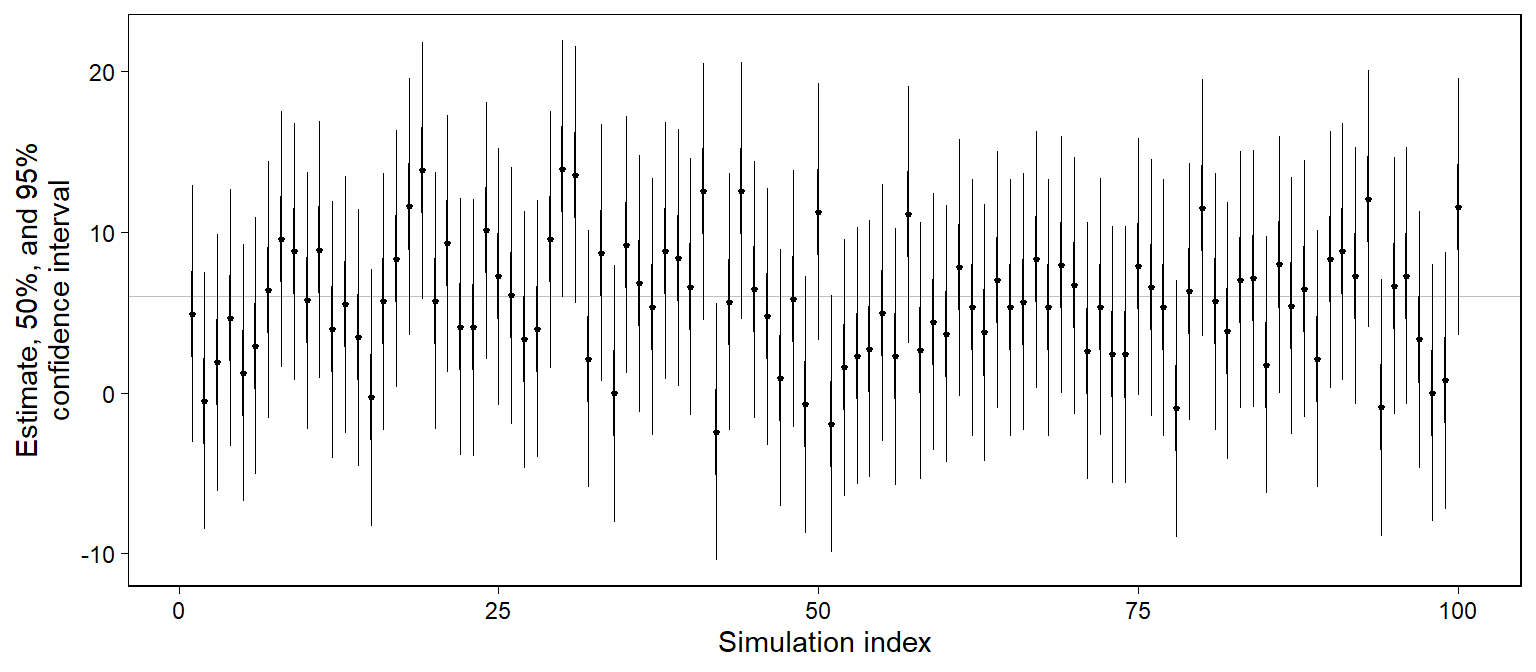
Figure 4.1: Simulation of coverage of confidence intervals: the horizontal line shows the true parameter value, and dots and vertical lines show estimates and confidence intervals obtained from 100 random simulations from the sampling distribution. If the model is correct, 50% of the 50% intervals and 95% of the 95% intervals should contain the true parameter value, in the long run.

4.2.12 Weighted averages

서로 다른 집단의 평균과 분산을 결합하여 가중평균을 구하듯, 가중평균에 대한 신뢰구간도 구할 수 있다 (Gelman, Hill, and Vehtari 2020: 54).

4.3 Bias and unmodeled uncertainty

모델이 참일 경우, 측정이 편향되지 않았을 경우, 무작위로 추출된 표본일 경우, 무작위화가 전제된 실험일 경우, 앞서 논의한 추론은 모두 일관된 결과를 내놓게 된다. 그러나 실제의 데이터 수집은 모두 불완전하므로 우리는 추론과 예측에 있어서 모델 오차의 가능성을 포함하게 된다 (Gelman, Hill, and Vehtari 2020: 55).

4.3.1 Bias in estimation

즉, 평균적으로 추정치가 맞다면, 우리는 추정치가 불편향(unbiased)하다고 한다.

• 예를 들어, 미국의 성인을 대상으로 하는 단순무작위표본이 있다고 하고, 각 응답자들은 하루에 TV를 몇 시간 보는지에 대해 응답하였다고 하자. 응답자들이 모두 정확하게 응답하였다고 할 때, 표본의 평균응답은 모집단의 평균 시청시간에 대한 불편추정량이 된다.

• 여성이 남성보다 더 응답을 많이 했다고 할때, 표본은 평균적으로 여성을 과대대표하게 되며, 여성이 평균적으로 남성보다 TV를 덜 시청한다는 결론은 모집단의 비율에 대해 “편향된”(biased) 추정량이 되는 것이다.

4.3.2 Adjusting inferences to account for bias and unmodeled uncertainty

통계모델에 포함하지 않은/포함할 수 없는 오차를 어떻게 설명할 수 있을까? 일반적으로 세 가지 방법으로 우리는 이 문제를 다룰 수 있다: (1) 데이터 수집의 질을 향상시키는 것, (2) (불확실성을 포함하는) 모델을 확장시키는 것, (3) 모델에 포함되지 않은 오차, 불확실성을 보다 명확하게 설명하는 것이 바로 그것이다(Gelman, Hill, and Vehtari 2020: 56).

4.4 Statistical significance, hypothesis testing, and statistical errors

데이터를 분석할 때 한 가지 주의해야할 것은 재현되지 않는 결론을 내리는 실수를 하거나, 또는 모집단에서의 실제 패턴을 반영하지 못하는 실수를 하는 것이다. 가설검정과 오차분석에 대한 통계이론은 추론과 의사결정이라는 맥락에서 이러한 가능성들을 계량화하고자 발전된 것이다(Gelman, Hill, and Vehtari 2020: 57).

4.4.1 Statistical significance

통계적 유의성은 통상적으로 가설검정의 맥락에서 영가설(null hypothesis), 또는 효과가 없을 것이라는 것을 보여주는 특정한 값(prespecified value)에 비해 \(p\)-값이 0.05보다 작은지로 정의된다. 적합된 회귀모델로 얘기하자면, 이러한 논리는 회귀계수의 추정치가 효과가 없을 것이라는 의미의 0과 비교하여 최소 2 표준오차만큼 차이가 나는지 여부를 가지고 통계적 유의성이 존재하는지를 판단하는 것이다(Gelman, Hill, and Vehtari 2020: 57).

Gelman, Hill, and Vehtari (2020) 은 동전을 20번 던졌을 때, 8번 앞면이 나오는 사건을 예시로 제시한다. 기존의 영가설은 앞면과 뒷면이 나올 확률이 각각 \(p = 0.5\)라고 할 때, 20번 중에서 8번, 즉 관측한 \(\hat p = 0.4\)가 통계적으로 \(p = 0.5\)와 유의미한 차이인지를 표준오차를 통해 \(\sqrt{\hat p (1 - \hat p) / n}\)로 계산하는 방식이다.

n <- 20
y <- 8
# the estimated probability
(p <- y / n)

## [1] 0.4

# the standard error
(se <- sqrt(p * (1 - p) / n))

## [1] 0.1095445

# the 95% CIs
p + c(-2 * se, 2 * se)

## [1] 0.180911 0.619089

이렇게 계산했을 때, 신뢰구간은 \(p = 0.5\)를 보함하고, 우리는 관측한 결과가 영가설과 통계적으로 유의미하게 다르지 않다고 결론을 내리게 된다.

4.4.2 Hypothesis testing for simple comparisons.

기존의 가설검정의 핵심적인 개념들을 간단한 예시를 통해 살펴보자. 콜레스테롤 수치를 낮추기 위한 두 약의 효과성을 비교하기 위한 무작위 실험을 수행했다고 하자. 처치 이후의 콜레스테롤 수치의 평균과 표준편차는 처치집단(\(n_T\))은 \(\bar y_T\), \(s_T\)이며, 통제집단(\(n_C\))은 \(\bar y_C\)와 \(s_C\)라고 하자(Gelman, Hill, and Vehtari 2020: 57).

4.4.2.1 Estimate, standard error, and degrees of freedom.

우리가 알고싶은 모집단의 특성, 모수는 \(\theta = \theta_T - \theta_C\)로, 두 집단의 실험 이후 콜레스테롤 수치의 차이에 대한 기대(expectation)라고 할 수 있다. 실험이 올바르게 수행되었다고 가정할 때, 추정치는 \(\hat \theta = \bar y_T - \bar y_C\)가 되며, 표준오차는 \(\text{se} (\hat \theta) = \sqrt{s_C^2 / n_C + s_T^2 / n_T}\)로 계산할 수 있다. 이때 약 95%의 신뢰구간은 \([\hat \theta \pm t_{n_C + n_T - 2}^{0.975} * \text{se} (\hat \theta)]\)이며, \(t_{df}^{0.975}\)는 \(df\)라는 자유도가 주어졌을 때, \(t\) 분포에서의 97.5 분위 즉, 1000개의 관측치가 있다면 975번째의 값을 의미한다(Gelman, Hill, and Vehtari 2020: 57).

4.4.2.2 Null and alternative hypotheses.

가설검정을 위해서는 영가설(null hypothesis)과 대안가설(alternative hypothesis)을 정의해야 한다. 여기에서 영기설은 \(\theta = 0\), 즉 처치집단과 통제집단의 처치 이후 콜레스테롤 수치가 같다는 것(\(\theta_T = \theta_C\))으로 두 약의 효과 차이가 없다는 것을 의미한다. 한편, 연구가설은 \(\theta \neq 0\)으로 처치집단과 통제집단의 처치 이후 콜레스테롤 수치가 같지 않다(\(\theta_T \neq \theta_C\))는 것을 의미한다.

가설검정은 영가설로 설정된 값으로부터 데이터로 얻은 값이 얼마나 떨어져 있는지를 요약해서 보여주는 검정통계치(test statistic)를 가지고 수행한다. 통상적인 검정 통계치는 \(t\)-값의 절대값으로, \(t = |\hat \theta| / \text{se}(\hat \theta)\), “양측 검정(two-sided test)”이라 불리는 가설검정을 사용한다. 이는 데이터로부터 얻은 값이 양수(positive)이던 음수(negative)이던 간에 상관없이 0으로부터 유의미한 차이를 가지고 있는지 여부만 본다는 것을 의미한다.

4.4.2.3 \(p\)-value.

가설검정에서 데이터가 영가설로부터 얼마나 떨어져 있는지는 \(p\)-값을 통해서도 볼 수 있다. \(p\)-값은 우리가 얼마나 극단적인 관측값을 확인할 수 있는지를 확률적으로 보여주는 수치이다. \(p\)-값은 \(\nu\)의 자유도를 가진 \(t\)-분포에서 영가설로부터 극단적으로 떨어진 값을 관측할 확률을 의미한다. R에서 theta_hat = \(\hat \theta\), se_theta = \(\text{se}(\hat \theta)\) n_C = \(n_C\), 그리고 n_T = \(n_T\)라고 할 때, \(p\)-값은 다음과 같이 구할 수 있다.

2 * (1 - pt(abs(theta_hat) / se_theta, df = n_C + n_T, ncp = 2))

4.4.3 Hypothesis testing: general formulation.

가설검정의 가장 간단한 형태는 영가설(\(H_0\))은 잠정적인 재현 데이터(\(y^\text{rep}\))에 대한 특정한 확률모델(\(p(y)\))로 나타난다. 가설검정을 수행하기 위해서 우리는 검정통계량, 데이터로부터 어떠한 함수적 관계를 통해 계산되는 \(T\)를 정의해야한다. 주어진 데이터 \(y\)에 대해 \(p\)-값은 \(\operatorname{Pr}(T(y^\text{rep}) \geq T(y))\)로 나타낼 수 있고, 이는 모델로 데이터의 관측된 값만콤 혹은 더 극단적인 값을 관측할 확률을 의미한다. 아까 위의 콜레스테롤 약을 예시로 들자면, 영가설은 효과가 없을 것이라고 할 때 \(p\)-값은 데이터로부터 영가설에 비해 얼마나 더 극단적인 값을 관측할 것인지의 확률을 보여주는 것으로, 극단적을 관측할 확률이 높을수록 우리는 데이터가 영가설(효과없음)과는 차이가 있는 값을 내놓을 것이라고 기대할 수 있게 되는 것이다.

회귀모델에서는 가설검정이 조금 더 복잡하다. 우리가 적합하고자 하는 모델을 \(p(y|x, \theta)\)라고 할 때, \(\theta\)는 계수와 잔차의 표준편차, 그리고 이외의 다른 모수들을 포함하는 것이라고 하자. 이때 영가설은 계수값이 0일 경우를 의미한다(Gelman, Hill, and Vehtari 2020: 58). 간단히 말하면 예측변수 \(x_1\)이 \(y\)와 맺는 관계가 0, 무관한 것과 같다는 것을 영가설로 설정하고 그 계수값이 표준오차를 고려했을 때 0으로부터 유의미하게 떨어져 있다면, 우리는 그 영가설을 기각하여 \(x_1\)과 \(y\)가 유의미한 관계를 맺고 있을 것이라고 결론을 내리게 되는 것이다.

4.4.4 Comparisons of parameters to fixed values and each other: interpreting confidence intervals as hypothesis tests.

모수가 0일 것(혹은 어떠한 고정된 값)이라는 가설은 그 모수를 포함한 모델을 적합하고 95% 신뢰구간을 분석함으로써 직접적으로 검정할 수 있다. 만약 우리가 추정한 신뢰구간이 0 (혹은 설정한 고정값을)을 포함하지 않는다면, 가설은 5%의 신뢰수준에서 기각된다고 말할 수 있다.

두 개의 모수가 서로 같은지 여부를 검정하는 것은 둘의 차이가 0인지를 검정하는 것과 같다. 따라서 모델 안에 두 모수 모두를 포함하고 그 두 모수의 차이에 대한 95% 신뢰구간을 분석하면 두 모수가 서로 같은지 여부를 검정할 수 있다. 하나의 모수에 대해 추론할 때와 마찬가지로 종종 가설검정 그 자체보다는 신뢰구간을 살펴보는 것이 더 흥미로울 수 있다. 예를 들어, 사형제에 대한 지지도가 약 \(6\pm2\) 퍼센트 감소했다고 할 때, 이렇게 추정된 차이의 크기는 그 변화의 신뢰구간이 0을 포함하지 않느냐 만큼이나 중요할 수 있다.

4.4.5 Type 1 and type 2 errors and why we don’t like talking about them.

통계적 검정은 1종오류(type 1 error)와 2종오류(type 2 error)로 이해할 수 있다.

• 1종오류: 영가설이 맞는데 그것을 거짓으로 기각할 확률.

  • 즉, 콜레스테롤 약이 효과가 없는게 맞는데 효과가 없다는 영가설을 기각해버렸을 오류를 의미한다.

• 2종오류: 영가설이 기각되어야 하는데, 기각에 실패할 확률.

  • 즉, 콜레스테롤 약의 효과에 차이가 있는데, 기각하지 못하여 두 약의 효과에 차이가 없다고 결론을 내릴 오류를 의미한다.

이론적으로는 이 두 오류에 대해 이해하고 있어야하지만, 이 두 오류가 사회과학 또는 과학적 연구 일반에 있어서 정확하게 들어맞기는 어렵다.¹¹ 그보다 1종오류와 2종오류 저변에 놓여있는 문제를 인지할 필요가 있는데,

4.4.6 4.4.6 Type M (magnitude) and type S (sign) errors.

S형 오류(type S error)는 추정된 효과의 부호(sign)가 모집단의 효과(진짜 효과; 추정하고자 한 효과; true effect)와 정반대로 나타나는 오류를 의미한다. M형 오류(type M error)는 추정된 효과의 크기가 진짜 효과의 크기와 크게 다를 때를 일컫는 오류이다. 통계적 기법으로 이 두 오류의 확률을 계산할수는 있지만, 앞의 1종오류, 2종오류와 마찬가지로 모집단의 효과를 우리가 관측하지 못하는 한, 완벽한 오류의 확인은 불가능하다.

4.4.7 Hypothesis testing and statistical practice.

일반적으로 영가설의 유의성 검정을 사용하지는 않는다. 실제 연구를 수행할 때, 영가설이 사실(\(H_0 = 0\), 또는 특정한 고정값과 “같다”)일 것이라고 기대하지는 않기 때문이다. 대개는 모든 처치가 어느 정도의 효과는 있으리라 생각한다. 그리고 어떠한 비교 혹은 관심을 갖고 있는 회귀계수가 정확히 0일 것이라고 기대하지도 않는다. 영가설 검정은 일종의 데이터 수집과 관련된 문제라고 할 수 있다: 충분한 규모의 표본이 있다면 어느 가설도 기각될 수 있다. 그리고 이론적으로 그러할 것이라고 믿지 않는 가설을 기각하기 위해 대규모의 데이터를 수집하는 것에는 의미가 없다(Gelman, Hill, and Vehtari 2020: 59). 즉, 영가설을 기각한다는 것—검정통계치가 특정 기준을 충족시킨다는 것이 모든 통계적 분석에 답이 되는 것은 아니다.

4.5 Problems with the concept of statistical significance

흔한 통계적 오류는 바로 통계적 유의성으로 비교해야할 내용을 정리해 유의하고 유의하지 않은 결과 간의 뚜렷한 차이를 도출해내는 것이다. 통계적 유의성으로만 결과를 살펴보는 데에는 다섯 가지 위험성이 존재한다. 그 중 두 가지는 명확하고, 나머지 셋은 잘 이해되지는 않는 위험이다(Gelman, Hill, and Vehtari 2020: 60).

4.5.1 Statistical significance is not the same as practical importance.

첫 번째 위험성은 통계적으로 유의한 것이 실제로 의미있는 것은 아닐 수 있다는 점이다. 우리가 효과의 크기를 확인하는 이유이기도 하다. 예를 들어, 탄 음식을 먹으면 암에 걸릴 확률이 증가한다는 가설에 대해 통계적으로 유의한 결과를 얻었다고 하자. 그런데 그 확률이 0.0000001%, 즉 한 번에 몇 십톤을 먹어야 발암 확률이 한 자리수로 증가한다는 결과라고 할 때, 과연 그 결과가 실질적으로 유의미하다고 할 수 있을까?

4.5.2 Non-significance is not the same as zero.

둘째, 통계적으로 유의미하지 않다는 것이 결코 효과가 없다는 것과 같은 의미는 아니다. 우리가 분석한 데이터가 영가설을 기각하지 못했을 뿐, 오히려 영가설을 “지지하는” 데이터일 수 있다.

4.5.3 The difference between “significant” and “not significant” is not itself statistically significant.

통계적으로 유의한 것과 유의하다는 것의 차이 그 자체는 통계적으로 유의하지 않다. 효과에 대한 추정치와 표준오차가 각각 \(25 \pm 10\)와 \(10 \pm 10\)인 두 독립적인 연구가 있다고 하자. 첫 번째 연구는 1% 신뢰수준에서 통계적으로 유의미하고 두 번째는 0으로부터 1 표준오차 떨어져 있는지를 기준으로 보았을 때에도 전혀 유의미하지 않았다. 이 두 연구의 결과를 비교해볼 때, 우리는 두 연구 간에 매우 큰 차이가 존재한다고 결론내리고 싶을 것이다. 하지만 사실 이 두 연구 결과의 차이는 통계적으로 유의하지조차 않다: 추정된 차이는 15이지만 표준편차가 \(\sqrt{10^2 + 10^2} = 14\)이기 때문이다(Gelman, Hill, and Vehtari 2020: 61).

4.5.4 Researcher degrees of freedom, \(p\)-hacking, and forking paths.

통계적 유의성의 또 다른 문제는 바로 여러 집단을 비교할 때 존재한다. 여러 가지 방식으로 데이터를 선택하고, 제외하고, 분석할 수 있다고 할 때, 실제로는 어떠한 기저의 패턴이 존재하지 않더라도 낮은 \(p\)-값을 얻는 것은 어렵지 않은 일이다. 여기서의 문제는 단순히 유의하지 않은 발견들이 출판되지 않는 “서류함 효과(file-drawer effect)”¹²만을 일컫는 것이 아니라 어떠한 연구도 데이터를 고딩하고 분석에 어떤 변수를 포함시킬지 결정하고, 어떻게 통계적 모델링을 할지 결정할 때, 연구자에게 주어지는 재량권(Gelman, Hill, and Vehtari (2020) 은 이를 연구자의 “자유도(degree of freedom)”이라고 적시하고 있다)과도 관련되어 있다(Gelman, Hill, and Vehtari 2020: 61). 예컨대, 연구자가 분석 과정에서 \(p\)-값이 낮은 결과/모델들만 선택적으로 보고할 때 생기는 문제 등을 생각해볼 수 있다.

4.5.5 The statistical significance filter.

마지막으로 통계적으로 유의미한 추정치가 과대추정되는 문제를 생각해볼 수 있다. M형 오류라고도 생각해볼 수 있는데, 바로 앞에서 언급한 서류함 효과를 생각해볼 수 있다. 일반적으로 출판된 연구의 경향성은 통계적으로 유의미한 결과들이 체계적으로 효과 크기를 과대추정하거나 결과를 왜곡하는 것으로 이어질 수 있다(Gelman, Hill, and Vehtari 2020: 62).

4.6 Moving beyond hypothesis testing

영가설 유의성 검정은 여러 문제를 가지고 있지만 특히나 정량연구에 있어서 실제적인 우려를 다루고 있다: 우리는 잡음이 많은 데이터(noisy data; 오차가 많은 데이터)로 인해 잘못된 결론을 내리지 않을 수 있기를 바라며, 가설검정은 오차에 대한 과대해석을 방지해줄 것을 기대한다. 어떻게 하면 통계적 유의성에 바탕을 둔 기존의 논리와 관련된 과잉확신과 과장의 문제를 피하되 통계적 논리로 얻을 수 있는 장점을 취할 수 있을까? Gelman, Hill, and Vehtari (2020, 66) 은 세 가지를 조언하고 있다.

• 가지고 있는 모든 데이터를 분석하라. 즉, 데이터의 특정한 부분만을 취사선택하여 분석하지 말고 연구 대상이 되는 데이터 전체를 분석하라는 것이다.

• 모든 비교 결과를 제시하라. 원하는 결과만을 취사선택하여 보여주지 말고, 유의하였건 유의하지 않았건 비교 결과를 모두 제시하여 연구의 투명성을 제고하고 일종의 효과의 과대추정 편향 보고를 지양하라는 것이다.

• 마지막으로 데이터를 공개할 수 있으면 가급적 공개하라는 것이다. 이는 다른 이들이 그 데이터를 통해 동일한 절차 혹은 다른 절차로 결과를 재현할 수 있느냐, 즉 과학적 연구의 재현가능성을 제고하는 데 기여할 수 있다.

References

Gelman, Andrew, Jennifer Hill, and Aki Vehtari. 2020. Regression and Other Stories. Cambridge University Press.

---

9. Gelman, Hill, and Vehtari (2020, 49)에서는 “Measurement error need not be additive”라고 서술하고 있다. 논리적으로 관계는 크게 두 가지로 나타낼 수 있다. 기호로 보자면 \(+\)와 \(\times\)가 바로 그것이다. \(+\)는 “또는 (OR)”과 같은 뜻으로 \(a+b\)라고 할 경우 \(a\)와 \(b\)는 서로 독립적인 관계라는 것을 의미한다. 한편, \(a\times b\)에서 \(\times\)는 “그리고 (AND)”의 의미로, \(a\)와 \(b\)가 서로 연관되어 있다는 것을 의미한다. 집합의 개념으로 이해하면 쉽다. 만약 \(a\)라는 집합과 \(b\)라는 집합이 있을 때, \(a+b\)는 \(a\cup b\)를 의미하며, 반대로 \(a\times b\)는 \(a\cap b\)를 의미한다. 따라서 Gelman, Hill, and Vehtari (2020, 49)의 표현은 오차항이 항상 다른 변수들과 독립적인 관계에 놓이는 것은 아니다, 즉 오차항이 다른 예측변수들과도 상관성이 있을 수 있다는 것을 시사한다.↩︎

10. 생성모델이란 데이터 \(X\)가 생성되는 과정을 두 개의 확률모형, 즉 \(\Pr(Y)\), \(\Pr(X|Y)\)으로 정의하고, 베이즈룰을 사용해 \(\Pr(Y|X)\)를 간접적으로 도출하는 모델이라고도 할 수 있다.↩︎

11. 과연 그 결과가 오류인지 아닌지, 모집단을 관측할 수 없는 우리로써는 판단이 쉽지 않다.↩︎

12. 일부 연구 결과는 논문으로 완성되어 과학 저널에 실리지 못하고 끝내 서류함 속에 머문다는 뜻으로 기출판된 경험적 연구들의 효과가 일종의 과대추정되는 편향성을 가지고 있을 수 있다는 것이다.↩︎