Chapter 6 Background on regression modeling

순수하게 수학적인 측면에서 회귀모델은 두 가지 목적을 갖는다: 예측(prediction)과 비교(comparison)이다.

  1. 주어진 일련의 투입(설명변수/예측변수)을 가지고 결과(종속변수/결과변수)의 분포를 예측하는 것.

  2. 투입(설명변수/예측변수)의 서로 다른 값들에 대해 이 예측들이 어떻게 달라지는지를 집단 간 단순비교 혹은 인과효과의 추정 등을 통해 비교하는 것.

6.1 Regression models

가장 단순한 회귀모델은 하나의 예측변수를 가진 선형모델이다.

\[ \text{Basic regression model}: y = a + bx + \mathrm{error}. \]

\(a\)와 \(b\)는 계수(coefficients), 혹은 보다 일반적으로 모델의 모수(parameters라고 한다. 단순선형모델은 여러 가지 방식으로 정교해질(복잡해질) 수 있으며, 다음과 같은 내용들을 포함할 수 있다.

  • 추가적인 예측변수들(Additional predictors)

    • \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k + \mathrm{error}\)

    • 벡터-매트릭스 식으로는 \(y = X\beta + \mathrm{error}\)라고 쓸 수 있다.

  • 비선형모델(Nonlinear models): \(\log y = a + b \log x + \mathrm{error}\).

  • 비가산모델(Nonadditive models)

    • 예측변수 \(x_1\)과 \(x_2\) 간의 상호작용을 포함

    • \(\log y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1 x_2 + \mathrm{error}\).

  • 일반화선형모델(Generalized linear models)

    • 정규분포인데다 다른 예측변수들에 독립적인 오차들을 가지고 있어 적합이 되지 않는 이산형 종속변수나 다른 데이터에 사용하는 선형회귀모델.

  • 비모수모델(Nonparametric models)

    • 주어진 \(x\)에 따라 \(y\)의 예측값에 대해 자의적인 곡선을 그릴 수 잇게 하는 수많은 모수들을 포함하는 모델.

  • 멀티레벨모델(Multilevel models)

    • 회귀모델의 계수는 집단 또는 시뮬레이션에 따라서 변할 수 있다. 멀티레벨 모델은 하나 이상의 분석수준을 가진 모델을 의미한다.

  • 측정-오차 모델(Measurement-error models)

    • 예측변수 \(x\)와 결과변수 \(y\)가 오차와 함께 측정되고, 핵심 통계치 간의 관계를 추정하고자 할 때 사용하는 모델.

Gelman, Hill, and Vehtari (2020) 에서는 선형회귀모델 중 가산형(additive), 비선형(nonlinear), 비가산형(nonadditive, 곱산형; multiplicative), 그리고 일반화 선형 모델에 대해 다룬다.

6.2 Fitting a simple regression to fake data

20개의 관측치를 가지는 페이크데이터 \(y_i\)가 예측변수 \(x_i\)는 1부터 20까지의 값을 가지고, 절편은 \(a = 0.2\), 기울기는 \(b=0.3\), 오차는 평균 0, 표준편차(\(\sigma\))가 0.5인 정규분포를 따르는 모델 \(y_i = a + b x_i + \epsilon_i\)로부터 시뮬레이션된다고 하자. 우리는 이 모델로부터 약 2/3에 해당하는 관측치들이 \(\pm \text{표준오차}\) 범주에 위치한다고 할 때, 이같은 페이크데이터는 다음과 같이 만들 수 있다.

library(tidyverse)
x <- 1:20
n <- length(x)
a <- 0.2
b <- 0.3
sigma <- 0.5
y <- a + b * x + sigma * rnorm(n)

6.2.1 Fitting a regression and displaying the results

모델을 적합하기 위해서 예측변수와 종속변수를 포함하는 데이터프레임, fake를 만들어보자.

fake <- data.frame(x, y)

Gelman, Hill, and Vehtari (2020) 은 stan_glm()을 이용해서 일반화선형모델을 추정, 시뮬레이션된 계수의 중앙값과 mad sd를 계산해서 제시한다. 하지만 여기서는 일반적으로 사용하는 lm()을 사용하여 회귀모델을 추정한다.

fit_1 <- lm(y ~ x, data = fake)
summary(fit_1)
## 
## Call:
## lm(formula = y ~ x, data = fake)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.13428 -0.38216 -0.05455  0.43228  1.05894 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.21588    0.29055   0.743    0.467    
## x            0.30394    0.02425  12.531 2.51e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6255 on 18 degrees of freedom
## Multiple R-squared:  0.8972, Adjusted R-squared:  0.8914 
## F-statistic:   157 on 1 and 18 DF,  p-value: 2.506e-10

분석 결과, 추정된 절편은 약 0.16의 불확성을 가지고 평균적으로 0.29의 값을 가진다. 추정된 기울기는 0.01의 불확실성을 가지고 0.3의 평균값을 가진다. 잔차의 표준오차는 0.34이다.

fitted_1 <- broom::augment(fit_1)
a_hat <- coef(fit_1)[1]
b_hat <- coef(fit_1)[2]
fitted_1 %>% 
  ggplot(aes(x, y)) + 
  geom_point(size = 2, shape = 21) + 
  geom_abline(intercept = a_hat, slope = b_hat) + 
  labs(subtitle = "Data and fitted regression line") + 
  geom_text(aes(x = mean(x) + 3, y = a_hat + b_hat*mean(x)), 
            label = paste("y =", round(a_hat, 2), "+", 
                          round(b_hat, 2), "* x")) + 
  scale_y_continuous(breaks = c(seq(1, 7, 1))) + 
  theme_bw()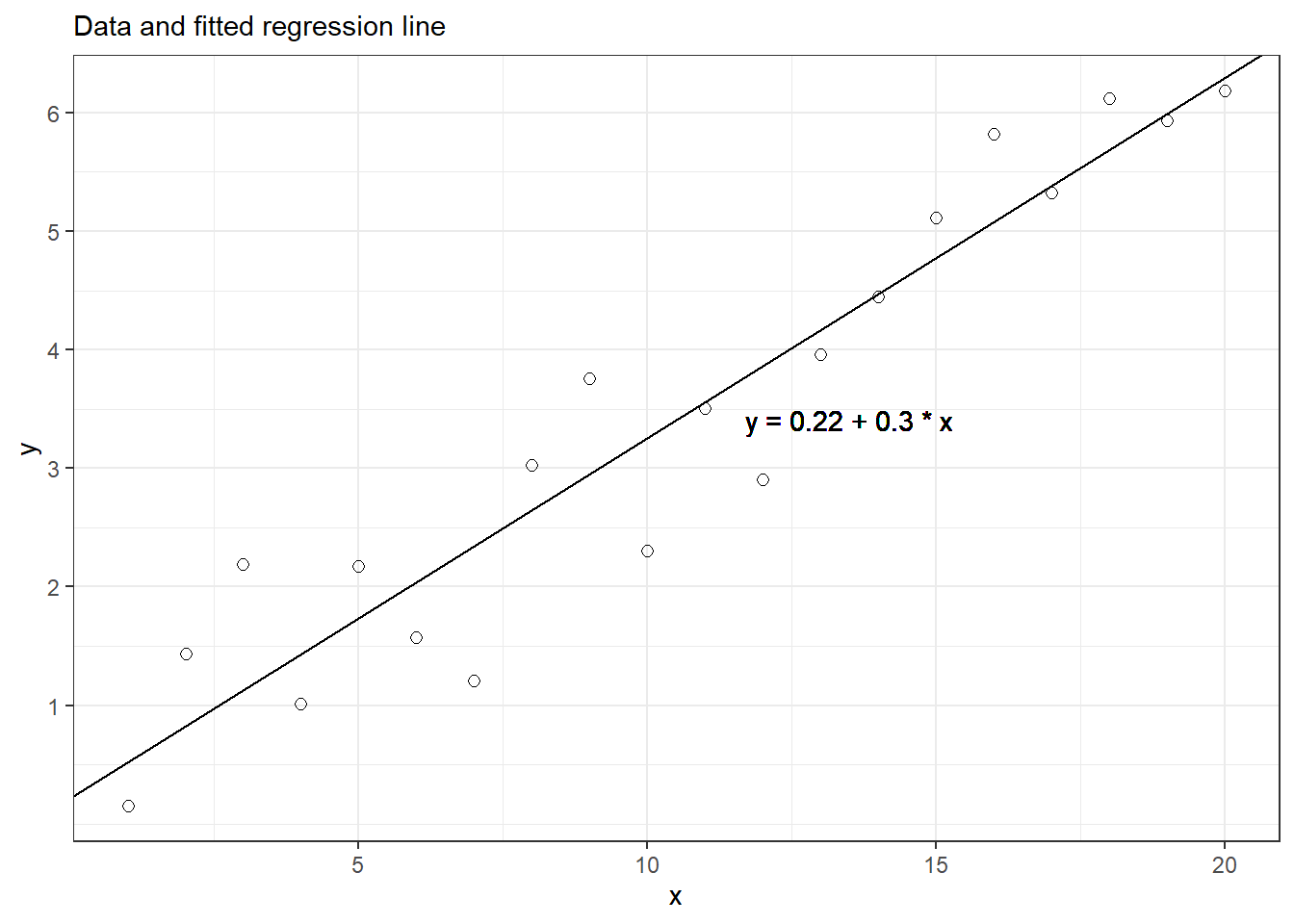
Simple example of a regression line fit to fake data. The 20 data points were simulated from the model, $y = 0.2 + 0.3x + \text{error}$, with errors that were independent and normally distributed with mean 0 and standard deviation 0.5.

Figure 6.1: Simple example of a regression line fit to fake data. The 20 data points were simulated from the model, \(y = 0.2 + 0.3x + \text{error}\), with errors that were independent and normally distributed with mean 0 and standard deviation 0.5.

6.2.2 Comparing estimates to assumed parameter values

페이크데이터에 모델을 적합하면, 모수에 대한 추정치와 가정된 값 간의 비교가 가능하다. 이 리딩노트에서는 stan을 이용한 시뮬레이션을 수행한 것이 아니기 때문에 \(\sigma\)에 대한 불확실성은 추정되지 않는다.

Table 6.1: After simulating 20 fake data points from a simple linear regression, \(y_i = a + b x_i + \epsilon_i\) , with errors \(\epsilon_i\) drawn from a normal distribution with mean 0 and standard deviation \(\sigma\), we then fit a linear regression to these data and obtain estimates and uncertainties for the three parameters from the model. We can then see that the estimates are roughly consistent with the specified parameter values
Parameter Assumed value Estimate Uncertainty
\(a\) 0.2 0.29 0.16
\(b\) 0.3 0.30 0.01
\(\sigma\) 0.5 0.34 NA

결과를 해석해보면 다음과 같다.

  • 우리는 모집단에서의 절편 \(a\)가 0.2일 것으로 기대했고, 페이크데이터로 모델이 추정한 결과는 0.29, 불확실성은 0.16이다.

  • 추정된 절편값과 모수로 가정한 값의 차이는 0.09이다. 하지만 절편에 대한 불확실성은 0.16이다.

  • 즉, 추정치와 실제 값(모수) 간의 차이는 1 표준오차보다 작다. 두 값의 차이는 불확실성으로 인해 나타날 수 있는 차이에 비해 오히려 작은 것이다. 과연 이 경우에 우리는 추정된 결과가 불확실성으로 인한 것일지 혹은 진짜 모수와 표본으로부터 얻은 결과가 차이가 있어서 나타난 차이일지 구분할 수 있을까?

6.3 Interpret coefficients as comparisons, not effects

회귀계수는 종종 “효과”라고 불리지만, 이 용어는 오해의 소지가 있다. 1816명의 응답자를 대상으로 한 설문데이터로 키(인치), 성별로 연간 소득(천 달러)을 예측하는 회귀모델을 적합하는 예제를 살펴보자.

earnings$earnk <- earnings$earn/1000
fit_2 <- lm(earnk ~ height + male, data=earnings)
summary(fit_2)
## 
## Call:
## lm(formula = earnk ~ height + male, data = earnings)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -31.99 -12.47  -3.53   7.05 368.66 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -25.8722    11.9615  -2.163  0.03068 *  
## height        0.6470     0.1852   3.493  0.00049 ***
## male         10.6327     1.4683   7.241 6.53e-13 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 21.39 on 1813 degrees of freedom
## Multiple R-squared:  0.09962,    Adjusted R-squared:  0.09862 
## F-statistic: 100.3 on 2 and 1813 DF,  p-value: < 2.2e-16

위의 분석 결과를 바탕으로 적합된 모델을 다시 써보면 다음과 같이 나타낼 수 있다.

\[ \text{earnings} = -25.9 + 0.6 \times \text{height} + 10.6 \times \text{male} + \text{error}. \]

\(\sigma\), 잔차의 표준편차는 21.4로 나타나는데 이 결과는 연간 소득 관측치의 약 68%가 선형 예측변수의 \(\pm \$21,400\) 범주 안에 위치하고, 약 95% 관측치가 \(2\pm2\times\$21,400 = \$42,800\)의 범주 안에 위치할 것이라는 점을 보여준다. 이때, 이 68%, 95%는 정규분포에 대한 특징에서 유도된 것이다.

데이터의 표준편차와 추정된 설명변동량의 비율을 비교하면 잔차의 표준편차에 대해 감을 잡을 수 있다.

R2 <- 1 - sigma(fit_2)^2 / sd(earnings$earnk)^2

\(R^2=0.10\)은 이 데이터에서 선형모델이 연간소득 변수의 약 10%를 설명한다는 것을 의미한다. 즉, 성별과 키만 가지고는 연간소득의 약 10%만 설명할 수 있다는 것이다.

한편, 적합된 모델을 과대해석하지 않도록 주의를 기울여야만 한다. 많은 가정들을 제외하더라도 예측변수와 결과변수 간의 관계-회귀계수를 “효과”라고 표현하는 것은 부적절하다. 왜냐하면 “효과”란 어떠한 “처치”나 “개임”과 관련되어 나타나는 변화로 정의하기 때문이다. “키가 연간 소득에 미치는 효과”가 $600이라고 말하는 것은 누군가의 키를 1인치 늘리면 그의 연간소득이 약 $600 증가할 것이라고 기대할 수 있다는 것을 의미한다. 그러나 이는 모델에서 추정된 결과는 아니다. 오히려 모델에서 추정된 것은 관측데이터를 통해 볼 수 있는 패턴-그 표본에서는 키가 큰 사람일수록 평균적으로 더 높은 연간소득을 가질 것이라는 것에 불과하다. 왜냐하면 실험 설계와 다르게 앞선 선형회귀모델에서는 키와 연간소득의 관계에서 연간소득에 영향을 미칠 수 있는 다른 변수들의 효과가 완벽하게 통제되지 않았기 때문이다.

그렇다면 적합된 모델에서 키에 대한 계수를 어떻게 생각할 수 있을까? “적합된 모델에서, 연간소득의 평균차이는 동일한 성별을 가지고 있지만 1인치 차이가 나는 두 사람을 비교했을 때, $600이다.”라고 말할 수 있다. 즉, 회귀모델의 가장 안전한 해석은 비교로 해석하는 것이다.

마찬가지로 추정된 “성별의 효과”가 $10,600이라고 말하는 것은 부적절하다. “적합된 모델에 따르면, 동일한 키를 가지고 있지만 성별만 다른 두 사람을 비교했을 때, 남성의 연간소득이 평균적으로 여성의 연간소득보다 $10,600 더 높을 것이다.”라고 해석하는 것이 적절하다.

정리하자면, 회귀모델은 예측을 위한 수리적 도구이다. 회귀계수는 때론 효과로 해석될 수 있지만, 그보다는 평균의 비교로 해석되는 것이 더 바람직하다.

6.4 Historical origins of regression

회귀(regression)이라는 개념을 Francis Galton으로부터 유래되었는데, 그는 사람의 키가 유전되는 것인지를 이해하기 위해 선형 모델을 적합해본 사람이다. 아이의 키가 부모로부터 유전되는가를 예측하면서, 그는 키가 큰 부모를 둔 아이의 키가 키가 작은 부모를 둔 아이들에 비하여 평균적으로 더 키가 큰 것을 확인하였다. 그 반대의 경우도 마찬가지였다. 즉, 사람의 키는 세대가 지남에 따라서 “평균으로 회귀”한다는 것을 발견했고, 회귀가 통계적 용어로 사용되기 시작한 것이다.

6.4.1 Daughters’ heights “regressing” to the mean

1903년 Karl Pearson과 Alice Lee의 유전에 관한 고전적 연구를 살펴보자.

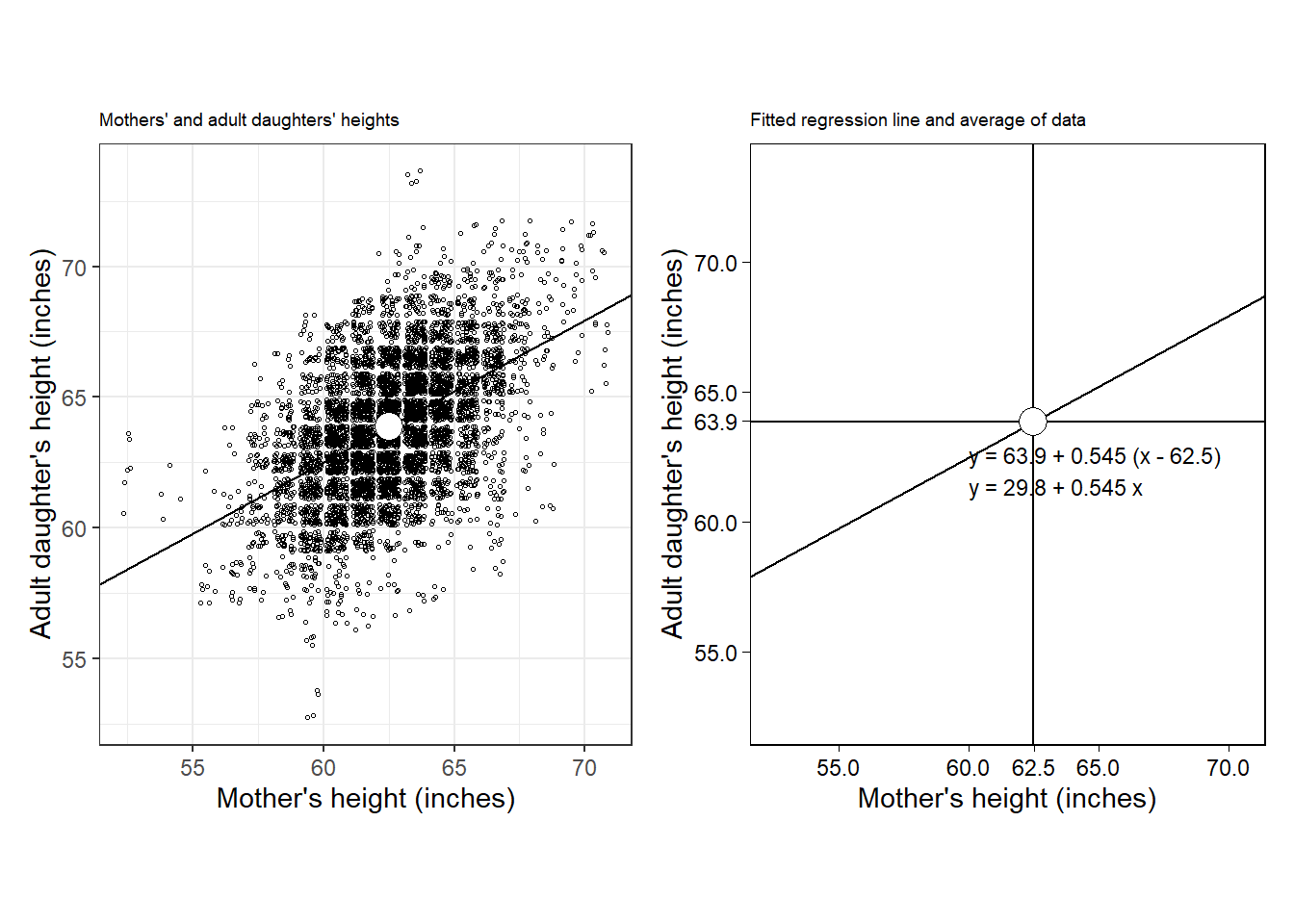
(a) Scatterplot adapted from data from Pearson and Lee (1903) of the heights of mothers and their adult daughters, along with the regression line predicting daughters’ from mothers’ heights. (b) The regression line by itself, just to make the pattern easier to see. The line automatically goes through the mean of the data, and it has a slope of 0.54, implying that, on average, the difference of a daughter’s height from the average (mean) of women’s heights is only about half the difference of her mother’s height from the average.

Figure 6.2: (a) Scatterplot adapted from data from Pearson and Lee (1903) of the heights of mothers and their adult daughters, along with the regression line predicting daughters’ from mothers’ heights. (b) The regression line by itself, just to make the pattern easier to see. The line automatically goes through the mean of the data, and it has a slope of 0.54, implying that, on average, the difference of a daughter’s height from the average (mean) of women’s heights is only about half the difference of her mother’s height from the average.

Figure 6.2a는 엄마와 딸의 키에 대한 데이터를 엄마의 키로부터 딸의 키를 예측하는 가장 잘 맞는 선-회귀선(regression line)에 따라서 배열한 것이다. 회귀선은 \(x\)와 \(y\)의 평균을 지나간다.

Figure 6.2b는 회귀선, \(y = 30 + 0.54x\)만을 보여준다. \(y = 30 + 0.54x + \text{error}\)라고도 쓸 수 있다. 여기서 오차를 포함하는 이유는 모델이 각각의 관측치들에 완벽하게 들어맞지는 않는다는 것을 강조하기 위함이다.

(a) Fitted regression line, $y = 30 + 0.54 x$, graphed using intercept and slope. (b) Difficulty of the intercept-slope formulation in the context of the data in the height example. The intercept of 30 inches corresponds to the predicted height of a daughter whose mother is a meaningless 0 inches tall.

Figure 6.3: (a) Fitted regression line, \(y = 30 + 0.54 x\), graphed using intercept and slope. (b) Difficulty of the intercept-slope formulation in the context of the data in the height example. The intercept of 30 inches corresponds to the predicted height of a daughter whose mother is a meaningless 0 inches tall.

Figure 6.3a는 회귀분석 결과를 절편-기울기의 형태로 나타내며 가장 시각화하기 쉬운 방식이다. 하지만 현실 세계를 기술하는 데 있어서 이러한 회귀선은 문제를 야기할 수 있다. Figure 6.3b를 보면 실제 데이터를 예측한 회귀선이 데이터가 존재하지 않는 지점까지 뻗어나가는 것을 확인할 수 있다. 현실 세계에서 키가 0인 사람은 존재하지 않는다. 선형모델을 통한 예측을 했을 때, 그 결과는 데이터에 미루어 합리적인 것이어야 한다. 어디까지가 우리가 실질적으로 이해할 수 있는 함의를 제공하는지를 판단하는 것은 연구자의 몫이 될 것이다.

6.4.2 Fitting the model in R

앞서 \(y = 30 + 54x\)가 가장 잘 들어맞는 선에 근사한다고 말했는데, 이때 “가장 잘 들어맞는다”는 것은 오차의 제곱합을 최소화하는 선(minimizing the sum of squared errors)이라는 것을 의미한다. 즉, 알고리즘에 따라 \(\sum^n_{i=1}(y_i - (a + bx_i))^2\)를 최소화하는 \(a\)와 \(b\)의 값을 구하는 것이다. 한 번 R을 통ㅎ애 알아보자.

id daughter_height mother_height
1 52.5 59.5
2 52.5 59.5
3 53.5 59.5
4 53.5 59.5
5 55.5 59.5

그러면 이제 어머니의 키로부터 딸의 키를 예측하는 회귀모델을 적합해보자. 데이터는 엄마-딸의 5524개 쌍의 키이며 모델은 세 개의 모수를 갖는다: 절편, 엄마 키에 대한 계수값, 그리고 잔차의 표준편차.

fit_1 <- lm(daughter_height ~ mother_height, data=heights)
summary(fit_1)
## 
## Call:
## lm(formula = daughter_height ~ mother_height, data = heights)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.7221 -1.4468  0.0981  1.5532  9.0981 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   29.79841    0.79034   37.70   <2e-16 ***
## mother_height  0.54494    0.01264   43.12   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.262 on 5522 degrees of freedom
## Multiple R-squared:  0.2519, Adjusted R-squared:  0.2518 
## F-statistic:  1860 on 1 and 5522 DF,  p-value: < 2.2e-16

데이터를 가지고 그래프를 한 번 그려보자. 1인치 단위로 산포도를 그리되, 각 변수를 확률변수로 만들 수 있다.

fig_1prac <- tibble(
  n = nrow(heights),
  mother_height_jitt = heights$mother_height + 
    runif(n, -0.5, 0.5),
  daughter_height_jitt = heights$daughter_height + 
    runif(n, -0.5, 0.5))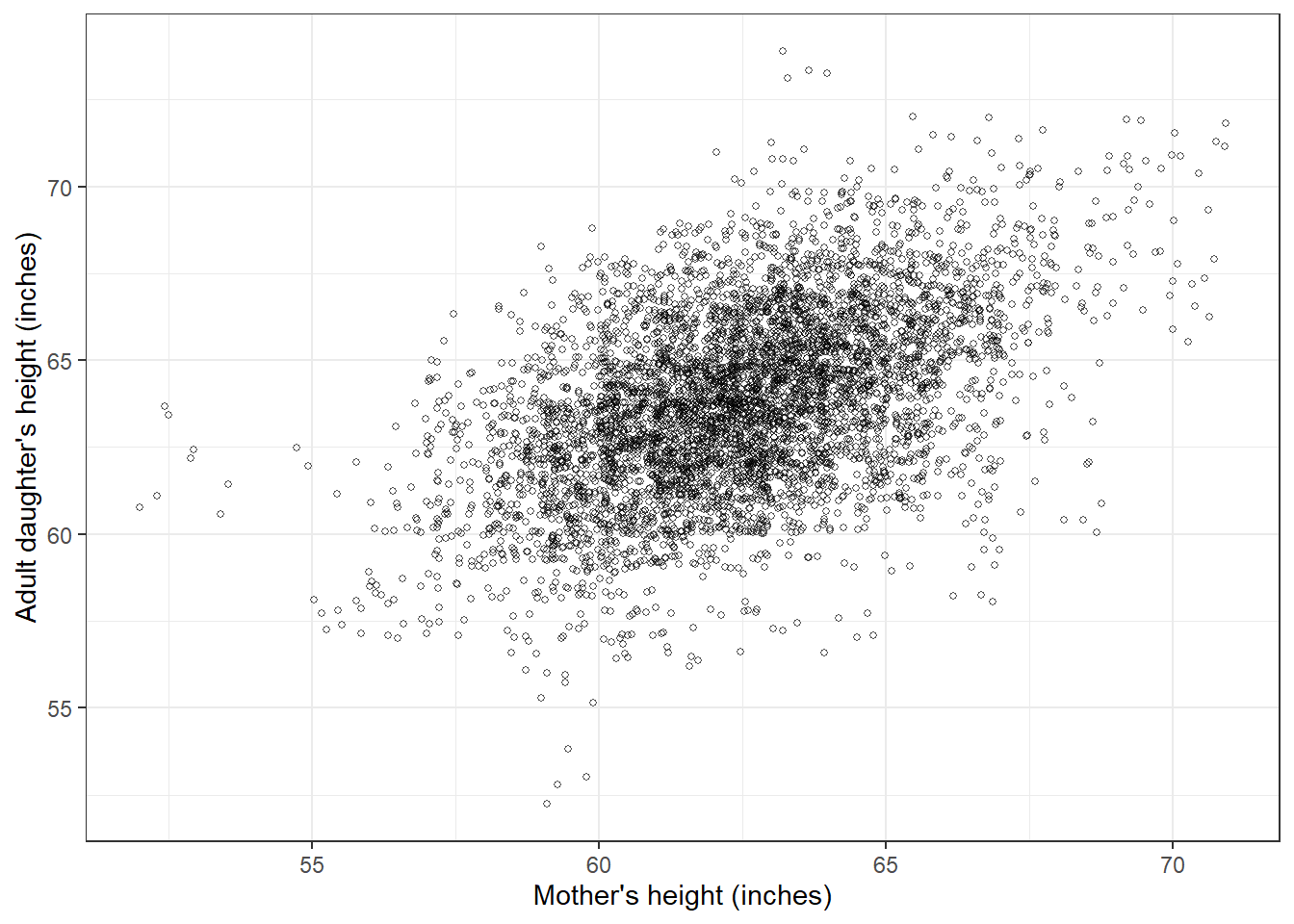

여기에다가 회귀모델에서 계수들을 추출해서 예측선을 플롯에 더해주면 된다.

a_hat <- coef(fit_1)[1]
b_hat <- coef(fit_1)[2]

fig_1prac %>% 
  ggplot(aes(mother_height_jitt, daughter_height_jitt)) + 
  geom_point(size = 1, shape = 21, alpha = 2/3) + 
  geom_abline(intercept = a_hat, slope = b_hat) + 
  labs(x = "Mother's height (inches)",
       y = "Adult daughter's height (inches)") + 
  theme_bw()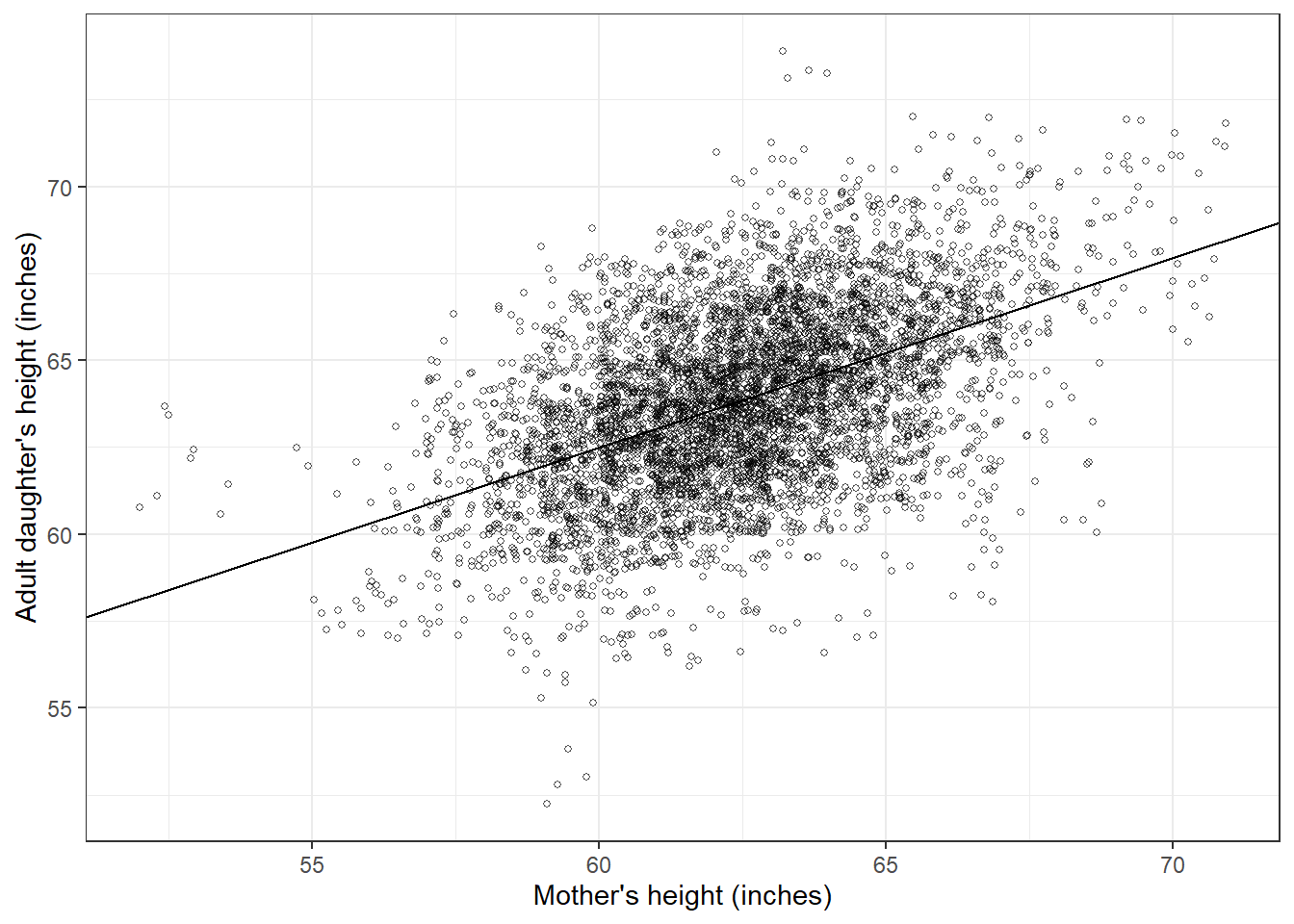

이 결과는 위의 Figure 6.2a와 동일하다.

6.5 The paradox of regression to the mean

그렇다면 과연 “키가 평균으로 회귀하는가?” Figure 6.2에서 나타나는 0.54라는 기울기는, 아니 사실 1보다 큰 모든 기울기는 사실 모순적으로 보인다. 만약 키가 큰 어머니가 키가 큰 딸을 가질 가능성이 크고, 키가 작은 어머니는 키가 작은 딸을 가질 가능성이 크다면, 딸들은 어머니들보다 평균에 수렴하고, 그러다보면 종래에는 모두 평균키가 된다는 이야기가 될 수 있다.

회귀모델의 함정이 이곳에 숨어잇다. 어머니의 키에 비해서 자녀의 예측된 키는 평균에 더 가까워지지만, 그것이 실제 키가 예측과 완벽하게 동일하다는 것을 의미하지는 않는다. 왜냐하면 현실 세계에서는 우리가 항상 모델에서 예측하지 못하는 “오차”가 존재하기 때문이다.

우리의 점추정치(점예측; 어떠한 한 점의 값으로 예측 한 것)은 평균으로 회귀하므로 그 계수값은 1보다 커질 수 있다. 그리고 점차 그 변동성(variation)은 감소한다(=평균과의 차이가 감소한다). 하지만 동시에 모델의 오차(예측의 불완전성)가 변동성을 더해 한 세대가 지나 다음 세대가 되더라도 키에 있어서 전체적인 변동성은 대략 일정해진다.

평균으로의 회귀는 안정적인 환경 하에서 예측이 불완전할 때라면 어떠한 형태로든 반드시 나타난다. 예측의 불완전성은 변동성을 초래하고, 전체적인 변동성을 일관되게 유지하기 위해 점추정치(예측)에 있어서의 회귀가 요구된다. 간단히 말하자면, 우리는 점점 평균키가 어느 정도인지에 대해서는 정확한 정보를 가지게 되지만 현실 세계 속에서 사람들의 키는 다양하게(오차를 가지고) 분포하기 때문에 전체적인 변동성-세대의 키는 한 세대가 지난다고 해서 모델처럼 뚜렷하게 변화하는 것이 아니다. 즉, 우리는 모델을 통해서 평균 키의 변화를 예측할 수 있지만, 그렇다고 해서 그것이 모든 관측치들-자녀들의 키가 다 평균으로 변해버린다는 것을 의미하지는 않는다.

6.5.1 How regression to the mean can confuse people about causal inference; demonstration using fake data

평균으로의 회귀라는 개념은 때로는 헷갈릴 수 있고, 종종 인과성으로 받아들여지는 오류를 야기한다. 이번에는 두 가지 종류의 시험을 치른 학생들에 대한 예제를 살펴보자.

Figure 6.4는 1,000명의 학생들의 중간고사와 기말고사 성적에 대한 가설적 데이터를 보여준다. 실제 데이터를 사용하기보다는 아래의 절차에 따라서 오차를 포함한 시뮬레이션된 시험 성적 데이터를 만들었다.

  1. 각 학생들은 평균 50, 표준편차 10이라는 분포에 실제 실력이 위치하고 있을 것으로 가정한다.

  2. 각 학생들의 중간고사 성적은 두 가지 요소의 합이다: 학생의 실제 실력과 평균 0, 표준편차가 10인 분포를 따르는 주어진 시험에 대한 성적에서 나타날 수 있는 예측불가능한 확률적 요소가 바로 그것이다. 중간고사는 완벽한 측정도구라고 보기는 힘들다. 예측이 불가능한 요소가 반영되어 있으니까.

  3. 마찬가지로 기말고사 점수도 실제 실력과, 그와는 독립적인 확률적 요소로 이루어져 있다.

가설적인 시험 데이터를 한 번 만들어보자.

set.seed(2243)

n_sims <- 1000

exams <- 
  tibble(
    true_ability = rnorm(n_sims, mean = 50, sd = 10),
    noise_1 = rnorm(n_sims, mean = 0, sd = 10),
    noise_2 = rnorm(n_sims, mean = 0, sd = 10),
    midterm = true_ability + noise_1,
    final = true_ability + noise_2
  )

그리고 이제 데이터의 분포를 산포도를 통해 보여주고, 동시에 적합된 회귀선을 그려보자.

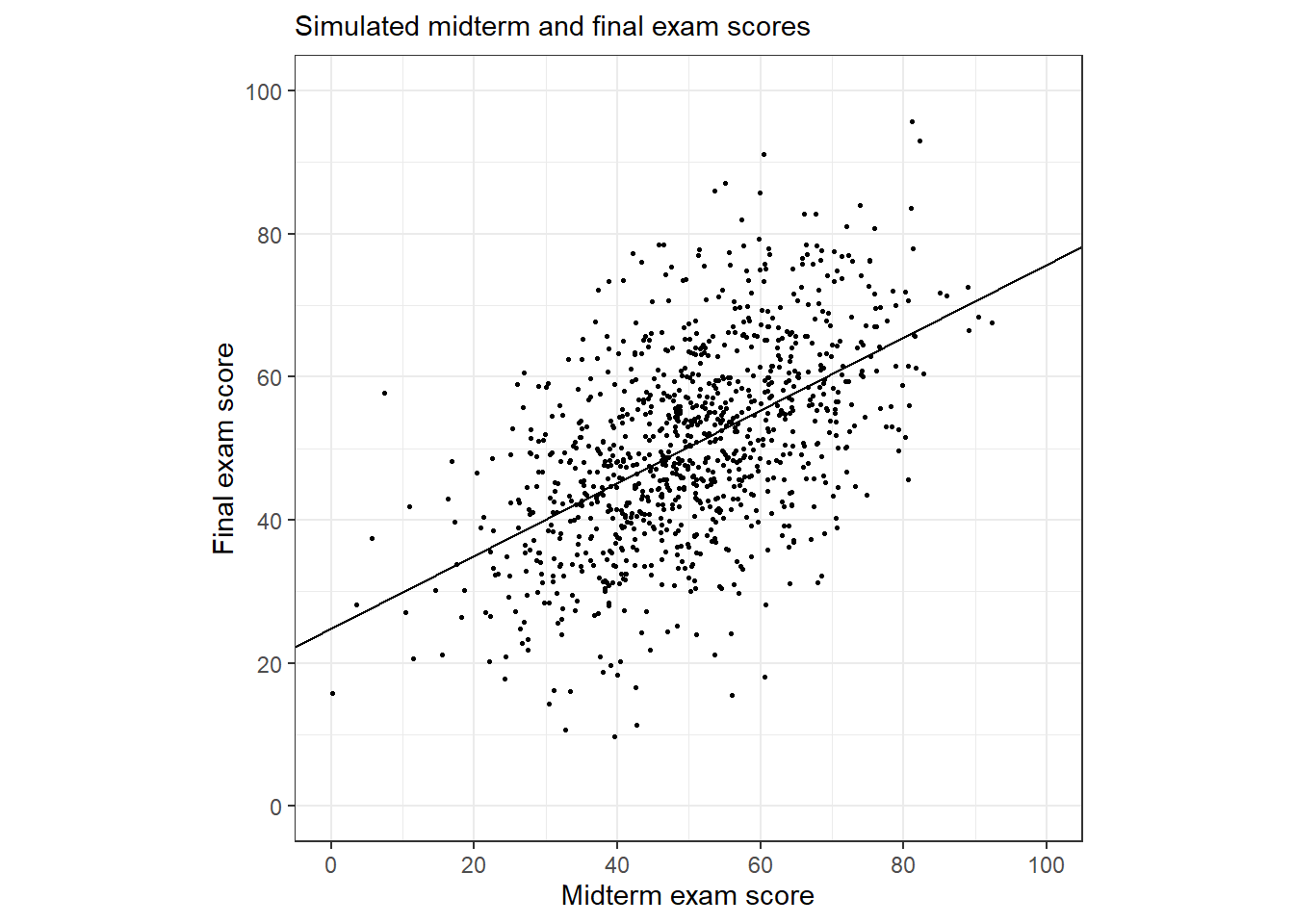
Scatterplot of simulated midterm and final exam scores with fitted regression line, which has a slope of 0.45, implying that if a student performs well on the midterm, he or she is expected to do not so well on the final, and if a student performs poorly on the midterm, he or she is expected to improve on the final; thus, regression to the mean.

Figure 6.4: Scatterplot of simulated midterm and final exam scores with fitted regression line, which has a slope of 0.45, implying that if a student performs well on the midterm, he or she is expected to do not so well on the final, and if a student performs poorly on the midterm, he or she is expected to improve on the final; thus, regression to the mean.

회귀분석 결과는 다음과 같다.

summary(fit)
## 
## Call:
## glm(formula = final ~ midterm, data = exams)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -37.732   -7.733   -0.233    7.275   35.487  
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 24.82407    1.33986   18.53   <2e-16 ***
## midterm      0.50864    0.02558   19.89   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 134.3792)
## 
##     Null deviance: 187250  on 999  degrees of freedom
## Residual deviance: 134110  on 998  degrees of freedom
## AIC: 7742.5
## 
## Number of Fisher Scoring iterations: 2

추정된 기울기는 약 0.5로 1보다 작다-평균으로의 회귀를 보여주는 결과이다. 중간고사에서 높은 점수를 받은 학생은 평균에 비해 약 절반 이상 높은 점수를 기말고사에 받는 경향이 나타났다. 중간고사에서 낮은 성적을 받은 학생은 기말고사에서도 평균보다 낮은 점수를 받는 경향이 나타났다.

  • 예를 들어, Figure 6.4에서 중간고사에서 0점을 받은 두 학생이 기말고사에서 각각 34, 42점을 받은 것을 확인할 수 있고, 반대로 중간고사에서 91점을받은 학생이 기말고사에서는 61점과 75점 사이를 받은 것을 확인할 수 있다.

이 결과를 인과적으로 해석하는 것은 자연스러워 보인다. 즉, 중간고사에서 점수를 잘 받은 학생들이 더 실력이 좋지만 실력에 자만해서 기말고사에서는 썩 잘하지 못한다는 식으로 말이다. 한편, 이러한 인과적 추론에 따르면 중간고사에서 성적이 나빴던 학생이 더 열심히 해서 기말고사에서는 성적을 높였다라고 할 수도 있다.

그러나 사실 데이터는 어떠한 효과를 목적으로 하는 모델에서 시뮬레이션된 것은 아니다. 중간고사와 기말고사 모두 실제 실력에 무작위 잡음(random noise; 오차)이 반영되었을 뿐이다.

평균으로의 회귀라는 경향성은 첫 번째와 두 번째 관측치들 간의 변동성에 따른 결과이다: 중간고사에서 점수를 매우 잘 받은 학생이 운이 좋거나 실력이 더 좋을 가능성이 크다. 마찬가지로 중간고사에서 망한 애들이 기말고사에서 열심히 준비해 평균보다 더 나은 성적을 냈다는 것도 말이 된다.

이 문제에서 핵심은 Figure 6.4의 데이터에 대한 “순진한” 해석이 종종 허위적인(spurious) 효과를 추론하도록 연구자를 유인할 수 있다는 것이다. 이 경우는 “중간고사를 잘 본 친구는 기말고사에 나태해져서 성적이 더 잘 안나오고, 중간고사를 망친 학생은 더 열심히 공부해서 기말고사에 더 나아졌을 것이다”라는 진술로 이해할 수 있다. 이러한 오류를 “회귀의 오류(regression fallacy)”라고 한다.

실제 사례로는 심리학자 Amos Tversky와 Daniel Kahneman의 1973년 연구가 있다.

항공학교에서 심리학자들의 조언에 따라 칭찬을 통해 성과를 제고하는 일종의 교육방침을 수립했는데, 강사들이 주장하기를 심리학자들이 이야기한 것과는 달리 칭찬해주니까 그 다음에 잘 못하더라는 것이었다.

이에 대한 설명은 다음과 같다.

항공 조작에 있어서 회귀란 필연적이다. 왜냐하면 조작 성과는 완벽하게 안정적이지 않고(reliable), 연이은 조작 간에 있어서 실력 향상은 더디기 때문이다. 따라서 한 번의 시도에 유독 좋은 성과를 낸 파일럿이 있다고 하더라도 다음 시도에서는 상대적으로 더 못할 가능성이 크다. 이는 첫 번째 성공에 대한 강사들의 반응(칭찬)에 무관하게 그러하다.\(\cdots\) 보통 뭘 잘할 때 칭찬하고, 못할 때 처벌한다. 하지만 회귀의 관점에서 보자면 처벌받고 난 이후에 더 잘할 가능성이 있고, 보상을 받고 난 이후에 더 못할 수 있다. 결과적으로, 처벌에 대한 보상, 그리고 보상에 대한 처벌에 일생동안 노출되어 있는 것이다.

이 이야기의 핵심은 예측에 대한 양적 이해(quantitative understanding)는 변동성(variation)과 인과성(causality)에 대한 근본적인 질적 혼동(qualitative confusion)을 명확하게 한다는 것이다.

  • 순수하게 수리적 관점에서 가장 조작을 잘 하는 파일럿은 실력이 다른 파일럿에 비하여 점점 떨어질 것이고, 가장 못하는 파일럿은 점차 잘 할 것이다.

  • 마찬가지로 모든 키 큰 엄마로부터 나온 딸들은 평균적으로 엄마들만큼은 크지 않을 것이고 평균으로 수렴하게 될 것이다.

6.5.2 Relation of “regression to the mean” to the larger themes of the book

앞서 설명한 회귀의 오류는 비교에 대한 잘못된 해석의 한 사례라고 볼 수 있다. 인과추론에 있어 보다 핵심적인 것은, “같은 것끼리 비교해야 한다”는 것이다.

중간고사와 기말고사 성적에 관련된 예제를 다시 생각해보자. 인과적 주장은 “중간고사에서 잘 못한 학생이 동기부여가 되어서 기말고사에 더 열심히 준비한 반면, 중간고사에서 잘 한 학생은 안심하고 노는 바람에 기말고사를 망치고 말았을 것이다”라고 할 수 있다. 이 비교에서 종속변수인 \(y\)는 기말고사 점수이고 예측변수 \(x\)는 중간고사 점수이다. 문제는 \(x\)에 있어서 한 단위가 변화한 학생을 비교할 때, \(y\)에 있어서 \(\frac{1}{2}\)만큼의 차이를 기대할 수 있다는 것에 있다.

이 결과는 기울기가 1인 경우와 비교되었기 때문에 나타난 결과이다. 회귀분석 결과와 Figure 6.4에서 나타난 경험적 패턴은 암묵적인 디폴트 모델, 중간고사와 기말고사 성적이 모두 같다라고 보는 모델과 비교한 것이다. 그러나 기울기가 1인 모델과 0.5인 모델 간의 비교는 부적절하다. 왜냐하면 디폴트 모델 자체가 문제가 있기 때문이다. 우리는 중간고사 기말고사가 어떠한 의도적 개입이 존재하지 않았을 때, 완전히 동일할 것이라고 생각할 그 어떠한 근거도 가지고 있지 않기 때문이다.

결국 Gelman, Hill, and Vehtari (2020) 은 이 부분에서 회귀분석이 경험적 경향성에 대한 정보는 줄 수 있지만 인과적 관계를 담보해주지 않는다는, “Association does not mean causation”이라는 말을 굉장히 돌려돌려 여러가지 방식으로 다른 표현을 가지고 설명해주고 있다.

References

Gelman, Andrew, Jennifer Hill, and Aki Vehtari. 2020. Regression and Other Stories. Cambridge University Press.