• GHV
  • 1 Overview
    • 1.1 The three challenges of statistics
    • 1.2 Why learn regression?
    • 1.3 Some examples of regression
      • 1.3.1 A randomized experiment on the effect of an educational television program
      • 1.3.2 Comparing the peacekeeping and gun-control studies
    • 1.4 Challenges in building, understanding, and interpreting regressions
      • 1.4.1 Regression to estimate a relationship of interest
      • 1.4.2 Regression to adjust for differences between treatment and control groups
      • 1.4.3 Interpreting coefficients in a predictive model
      • 1.4.4 Building, interpreting, and checking regression models
    • 1.5 Classical and Bayesian inference
      • 1.5.1 Information
      • 1.5.2 Assumptions
      • 1.5.3 Classical inference
      • 1.5.4 Bayesian inference
    • 1.6 Computing least squares and Bayesian regression
  • 2 Data and Measurement
    • 2.1 Examining where data come from
      • 2.1.1 Details of measurement can be important
    • 2.2 Validity and reliability
      • 2.2.1 Validity
      • 2.2.2 Reliability
      • 2.2.3 Sample selection
    • 2.3 All graphs are comparisons
      • 2.3.1 Simple scatterplots
      • 2.3.2 Displaying more information on a graph
      • 2.3.3 Multiple plots
      • 2.3.4 Grids of plots
      • 2.3.5 Applying graphical principles to numerical displays and communication more generally
      • 2.3.6 Graphics for understanding statistical models
      • 2.3.7 Graphs as comparisons
      • 2.3.8 Graphs of fitted models
    • 2.4 Data and adjustment: trends in mortality rates
  • 3 Some Basic Methods in Mathematics and Probability
    • 3.1 Weighted averages
    • 3.2 Vectors and matrices
    • 3.3 Graphing a line
    • 3.4 Exponential and power-law growth and decline; logarithmic and log-log relationships
    • 3.5 Probability distributions
      • 3.5.1 Mean and standard deviation of a probability distribution
      • 3.5.2 Normal distribution; mean and standard deviation
      • 3.5.3 Linear transformations
      • 3.5.4 Mean and standard deviation of the sum of correlated random variables
      • 3.5.5 Lognormal distribution
      • 3.5.6 Binomial distribution
      • 3.5.7 Poisson distribution
      • 3.5.8 Unclassified probability distribution
      • 3.5.9 Probability distributions for error
      • 3.5.10 Comparing distributions
    • 3.6 Probability modeling
      • 3.6.1 Using an empirical forecast
      • 3.6.2 Using an reasonable-seeming but inappropriate probability model
      • 3.6.3 General lessons for probability modeling
  • 4 Statistical Inference
    • 4.1 Sampling distributions and generative models
      • 4.1.1 Sampling, measurement error, and model error
      • 4.1.2 The sampling distribution
    • 4.2 Estimates, standard errors, and confidence intervals
      • 4.2.1 Parameters, estimands, and estimates
      • 4.2.2 Standard errors, inferential uncertainty, and confidence intervals
      • 4.2.3 Standard errors and confidence intervals for average and proportions
      • 4.2.4 Standard error and confidence interval for a proportion when \(y = 0\) or \(y = n\)
      • 4.2.5 Standard error for a comparison
      • 4.2.6 Sampling distribution of the sample mean and standard deviation; normal and \(\chi^2\) distributions
      • 4.2.7 Degrees of freedom
      • 4.2.8 Confidence intervals from the \(t\) distribution
      • 4.2.9 Inference for discrete data
      • 4.2.10 Linear transformations
      • 4.2.11 Comparisons, visual and numerical
      • 4.2.12 Weighted averages
    • 4.3 Bias and unmodeled uncertainty
      • 4.3.1 Bias in estimation
      • 4.3.2 Adjusting inferences to account for bias and unmodeled uncertainty
    • 4.4 Statistical significance, hypothesis testing, and statistical errors
      • 4.4.1 Statistical significance
      • 4.4.2 Hypothesis testing for simple comparisons.
      • 4.4.3 Hypothesis testing: general formulation.
      • 4.4.4 Comparisons of parameters to fixed values and each other: interpreting confidence intervals as hypothesis tests.
      • 4.4.5 Type 1 and type 2 errors and why we don’t like talking about them.
      • 4.4.6 4.4.6 Type M (magnitude) and type S (sign) errors.
      • 4.4.7 Hypothesis testing and statistical practice.
    • 4.5 Problems with the concept of statistical significance
      • 4.5.1 Statistical significance is not the same as practical importance.
      • 4.5.2 Non-significance is not the same as zero.
      • 4.5.3 The difference between “significant” and “not significant” is not itself statistically significant.
      • 4.5.4 Researcher degrees of freedom, \(p\)-hacking, and forking paths.
      • 4.5.5 The statistical significance filter.
    • 4.6 Moving beyond hypothesis testing
  • 5 Simulation
    • 5.1 Simulation of discrete probability models
      • 5.1.1 How many girls in 400 births?
      • 5.1.2 Accounting for twins
    • 5.2 Simulation of continuous and mixed discrete/continuous models
      • 5.2.1 Simulation in R using custom-made functions
    • 5.3 Summarizing a set of simulations using median and median absolute deviation
    • 5.4 Bootstrapping to simulate a sampling distribution
      • 5.4.1 Choices in defining the bootstrap distribution
      • 5.4.2 Limitations of bootstrapping
    • 5.5 Fake-data simulation as a way of life
  • 6 Background on regression modeling
    • 6.1 Regression models
    • 6.2 Fitting a simple regression to fake data
      • 6.2.1 Fitting a regression and displaying the results
      • 6.2.2 Comparing estimates to assumed parameter values
    • 6.3 Interpret coefficients as comparisons, not effects
    • 6.4 Historical origins of regression
      • 6.4.1 Daughters’ heights “regressing” to the mean
      • 6.4.2 Fitting the model in R
    • 6.5 The paradox of regression to the mean
      • 6.5.1 How regression to the mean can confuse people about causal inference; demonstration using fake data
      • 6.5.2 Relation of “regression to the mean” to the larger themes of the book
  • 7 Linear regression with a single predictor
    • 7.1 Example: predicting presidential vote share from the economy
      • 7.1.1 Fitting a linear model to data
      • 7.1.2 Understanding the fitted model
      • 7.1.3 Graphing the fitted regression line
      • 7.1.4 Using the model to predict
    • 7.2 Checking the model-fitting procedure using fake-data simulation
      • 7.2.1 Step 1: Creating the pretend world
      • 7.2.2 Step 2: Simulating fake data
      • 7.2.3 Step 3: Fitting the model and comparing fitted to assumed values
      • 7.2.4 Step 4: Embedding the simulation in a loop
    • 7.3 Formulating comparisons as regression models
      • 7.3.1 Estimating the mean is the same as regressing on a constant term
      • 7.3.2 Estimating a difference is the same as regressing on an indicator variable
  • 8 Fitting regression models
    • 8.1 Least squares, maximum likelihood, and Bayesian inference
      • 8.1.1 Least squares
      • 8.1.2 Estimation of residual standard deviation \(\sigma\)
      • 8.1.3 Computing the sum of squares directly
      • 8.1.4 Maximum likelihood
      • 8.1.5 Where do the standard errors come from? Using the likelihood surface to assess uncertainty in the parameter estimates
      • 8.1.6 Bayesian inference
      • 8.1.7 Point estimate, mode-based approximation, and posterior simulations
    • 8.2 Influence of individual points in a fitted regression
    • 8.3 Least squares slope as a weighted average of slopes of pairs
    • 8.4 Comparing two fitting functions: lm and stan_glm
      • 8.4.1 Reproducing maximum likelihood using stan_glm with flat priors and optimization
      • 8.4.2 Running lm
      • 8.4.3 Confidence intervals, uncertainty intervals, compatibility intervals
  • 9 Prediction and Bayesian inference
    • 9.1 Propagating uncertainty in inference using posterior simulations
      • 9.1.1 Uncertainty in the regression coefficients and implied uncertainty in the regression line
      • 9.1.2 Using the matrix of posterior simulations to express uncertainty about a parameter estimate or function of parameter estimates
    • 9.2 Prediction and uncertainty: predict, posterior_linpred, and posterior_predict
      • 9.2.1 Point prediction using predict
      • 9.2.2 Linear predictor with uncertainty using posterior_linpred or posterior_epred
      • 9.2.3 Predictive distribution for a new observation using posterior_predict
      • 9.2.4 Prediction given a range of input values
      • 9.2.5 Propagating uncertainty
      • 9.2.6 Simulating uncertainty for the linear predictor and new observations
    • 9.3 Prior information and Bayesian synthesis
      • 9.3.1 Expressing data and prior information on the same scale
      • 9.3.2 Bayesian information aggregation
      • 9.3.3 Different ways of assigning prior distributions and performing Bayesian calculations
    • 9.4 Example of Bayesian inference: beauty and sex ratio
      • 9.4.1 Prior information
      • 9.4.2 Prior estimate and standard error
      • 9.4.3 Data estimate and standard error
      • 9.4.4 Bayes estimate
      • 9.4.5 Understanding the Bayes estimate
    • 9.5 Uniform, weakly informative, and informative priors in regression
      • 9.5.1 Uniform prior distribution
      • 9.5.2 Default prior distribution
      • 9.5.3 Weakly informative prior distribution based on subject-matter knowledge
      • 9.5.4 Example where an informative prior makes a difference: Beauty and sex ratio
  • 10 Linear regression with multiple predictors
    • 10.1 Adding predictors to a model
      • 10.1.1 Starting with a binary predictor
      • 10.1.2 A single continuous predictor
      • 10.1.3 Including both predictors
      • 10.1.4 Understanding the fitted model
    • 10.2 Interpreting regression coefficients
      • 10.2.1 It’s not always possible to change one predictor while holding all others constant
      • 10.2.2 Counterfactual and predictive interpretations
    • 10.3 Interactions
      • 10.3.1 When should we look for interactions?
      • 10.3.2 Interpreting regression coefficients in the presence of interactions
    • 10.4 Indicator variables
      • 10.4.1 Centering a predictor
      • 10.4.2 Including a binary variable in a regression
      • 10.4.3 Using indicator variables for multiple levels of a categorical predictor
      • 10.4.4 Changing the baseline factor level
      • 10.4.5 Using an index variable to access a group-level predictor
    • 10.5 Formulating paired or blocked designs as a regression problem
      • 10.5.1 Completely randomized experiment
      • 10.5.2 Paired design
      • 10.5.3 Block design
    • 10.6 Example: uncertainty in predicting congressional elections
      • 10.6.1 Background
      • 10.6.2 Data issues
      • 10.6.3 Fitting the model
      • 10.6.4 Simulation for inferences and predictions of new data points
      • 10.6.5 Predictive simulation for a nonlinear function of new data
      • 10.6.6 Combining simulation and analytic calculations
    • 10.7 Mathematical notation and statistical inference
      • 10.7.1 Predictors
      • 10.7.2 Regression in vector-matrix notation
      • 10.7.3 Two ways of writing the model
      • 10.7.4 Nonidentified parameters, collinearity, and the likelihood function
      • 10.7.5 Hypothesis testing: why we do not like \(t\) tests and \(F\) tests
    • 10.8 Weighted regression
      • 10.8.1 Three models leading to weighted regression
      • 10.8.2 Using a matrix of weights to account for correlated errors
    • 10.9 Fitting the same model to many datasets
      • 10.9.1 Predicting party identification
  • 11 Assumptions, diagnostics, and model evaluation
    • 11.1 Assumptions of regression analysis
      • 11.1.1 Failures of the assumptions
      • 11.1.2 Causal inference
    • 11.2 Plotting the data and fitted model
      • 11.2.1 Displaying a regression line as a function of one input variable
      • 11.2.2 Displaying two fitted regression lines
      • 11.2.3 Displaying uncertainty in the fitted regression
      • 11.2.4 Displaying using one plot for each input variable
      • 11.2.5 Plotting the outcome vs. a continuous predictor
      • 11.2.6 Forming a linear predictor from a multiple regression
    • 11.3 Residual plots
      • 11.3.1 Using fake-data simulation to understand residual plots
      • 11.3.2 A confusing choice: plot residuals vs. predicted values, or residuals vs. observed values?
      • 11.3.3 Understanding the choice using fake-data simulation
    • 11.4 Comparing data to replications from a fitted model
      • 11.4.1 Example: simulation-based checking of a fitted normal distribution
    • 11.5 Example: predictive simulation to check the fit of a time-series model
      • 11.5.1 Fitting a first-order autoregression to the unemployment series
      • 11.5.2 Simulating replicated datasets
      • 11.5.3 Visual and numerical comparisons of replicated to actual data
    • 11.6 Residual standard deviation \(\sigma\) and explained variance \(R^2\)
      • 11.6.1 Difficulties in interpreting residual standard deviation and explained variance
      • 11.6.2 Bayesian \(R^2\)
    • 11.7 External validation: checking fitted model on new data
    • 11.8 Cross validation
      • 11.8.1 Leave-one-out cross validation
      • 11.8.2 Fast leave-one-out cross validation
      • 11.8.3 Summarizing prediction error using the log score and deviance
      • 11.8.4 Overfitting and AIC
      • 11.8.5 Interpreting differences in log scores
      • 11.8.6 Demonstration of adding pure noise predictors to a model
      • 11.8.7 \(K\)-fold cross validation
      • 11.8.8 Demonstration of \(K\)-fold cross validation using simulated data
      • 11.8.9 Concerns about model selection
  • 12 Transformations and regression
    • 12.1 Linear transformations
      • 12.1.1 Scaling of predictors and regression coefficients
      • 12.1.2 Standardization using z-scores
      • 12.1.3 Standardization using an externally specified population distribution
      • 12.1.4 Standardization using reasonable scales
    • 12.2 Centering and standardizing for models with interactions
      • 12.2.1 Centering by subtracting the mean of the data
      • 12.2.2 Using a conventional centering point
      • 12.2.3 Standardizing by subtracting the mean and dividing by 2 standard deviations
      • 12.2.4 Why scale by 2 standard deviations?
      • 12.2.5 Multiplying each regression coefficient by 2 standard deviations of its predictor
    • 12.3 Correlation and “regression to the mean”
      • 12.3.1 The principal component line and the regression line
      • 12.3.2 Regression to the mean
    • 12.4 Logarithmic transformations
      • 12.4.1 Earnings and height example
      • 12.4.2 Why we use natural log rather than log base 10
      • 12.4.3 Building a regression model on the log scale
      • 12.4.4 Further difficulties in interpretation
      • 12.4.5 Log-log model: transforming the input and outcome variables
      • 12.4.6 Taking logarithms even when not necessary
    • 12.5 Other transformations
      • 12.5.1 Square root transformations
      • 12.5.2 Idiosyncratic transformations
      • 12.5.3 Using continuous rather than discrete predictors
      • 12.5.4 Using discrete rather than continuous predictors
      • 12.5.5 Index and indicator variables
      • 12.5.6 Indicator variables, identifiability, and the baseline condition
    • 12.6 Building and comparing regression models for prediction
      • 12.6.1 General principles
      • 12.6.2 Example: predicting the yields of mesquite bushes
      • 12.6.3 Using the Jacobian to adjust the predictive comparison after a transformation
      • 12.6.4 Constructing a simpler model
    • 12.7 Models for regression coefficients
      • 12.7.1 Other models for regression coefficients
  • 13 Logistic regression
    • 13.1 Logistic regression with a single predictor
      • 13.1.1 Example: modeling political preference given income
      • 13.1.2 The logistic regression model
      • 13.1.3 Fitting the model using stan_glm and displaying uncertainty in the fitted model
    • 13.2 Interpreting logistic regression coefficients and the divide-by-4 rule
      • 13.2.1 Evaluation at and near the mean of the data
      • 13.2.2 The divide-by-4 rule
      • 13.2.3 Interpretation of coefficients as odds ratios
      • 13.2.4 Coefficient estimates and standard errors
      • 13.2.5 Statistical significance
      • 13.2.6 Displaying the results of several logistic regressions
    • 13.3 Predictions and comparisons
      • 13.3.1 Point prediction using predict
      • 13.3.2 Linear predictor with uncertainty using posterior_linpred
      • 13.3.3 Expected outcome with uncertainty using posterior_epred
      • 13.3.4 Predictive distribution for a new observation using posterior_predict
      • 13.3.5 Prediction given a range of input values
      • 13.3.6 Logistic regression with just an intercept
      • 13.3.7 Logistic regression with a single binary predictor
    • 13.4 Latent-data formulation
      • 13.4.1 Interpretation of the latent variables
      • 13.4.2 Nonidentifiability of the latent scale parameter
    • 13.5 Maximum likelihood and Bayesian inference for logistic regression
      • 13.5.1 Maximum likelihood using iteratively weighted least squares
      • 13.5.2 Bayesian inference with a uniform prior distribution
      • 13.5.3 Default prior in stan_glm
      • 13.5.4 Bayesian inference with some prior information
      • 13.5.5 Comparing maximum likelihood and Bayesian inference using a simulation study
    • 13.6 Cross validation and log score for logistic regression
      • 13.6.1 Understanding the log score for discrete predictions
      • 13.6.2 Log score for logistic regression
  • 14 Simulation
    • 14.1 Simulation of discrete probability models
      • 14.1.1 How many girls in 400 births?
      • 14.1.2 Accounting for twins
    • 14.2 Simulation of continuous and mixed discrete/continuous models
      • 14.2.1 Simulation in R using custom-made functions
    • 14.3 Summarizing a set of simulations using median and median absolute deviation
    • 14.4 Bootstrapping to simulate a sampling distribution
      • 14.4.1 Choices in defining the bootstrap distribution
      • 14.4.2 Limitations of bootstrapping
    • 14.5 Fake-data simulation as a way of life
  • 15 Simulation
    • 15.1 Simulation of discrete probability models
      • 15.1.1 How many girls in 400 births?
      • 15.1.2 Accounting for twins
    • 15.2 Simulation of continuous and mixed discrete/continuous models
      • 15.2.1 Simulation in R using custom-made functions
    • 15.3 Summarizing a set of simulations using median and median absolute deviation
    • 15.4 Bootstrapping to simulate a sampling distribution
      • 15.4.1 Choices in defining the bootstrap distribution
      • 15.4.2 Limitations of bootstrapping
    • 15.5 Fake-data simulation as a way of life
  • 16 Simulation
    • 16.1 Simulation of discrete probability models
      • 16.1.1 How many girls in 400 births?
      • 16.1.2 Accounting for twins
    • 16.2 Simulation of continuous and mixed discrete/continuous models
      • 16.2.1 Simulation in R using custom-made functions
    • 16.3 Summarizing a set of simulations using median and median absolute deviation
    • 16.4 Bootstrapping to simulate a sampling distribution
      • 16.4.1 Choices in defining the bootstrap distribution
      • 16.4.2 Limitations of bootstrapping
    • 16.5 Fake-data simulation as a way of life
  • 17 Simulation
    • 17.1 Simulation of discrete probability models
      • 17.1.1 How many girls in 400 births?
      • 17.1.2 Accounting for twins
    • 17.2 Simulation of continuous and mixed discrete/continuous models
      • 17.2.1 Simulation in R using custom-made functions
    • 17.3 Summarizing a set of simulations using median and median absolute deviation
    • 17.4 Bootstrapping to simulate a sampling distribution
      • 17.4.1 Choices in defining the bootstrap distribution
      • 17.4.2 Limitations of bootstrapping
    • 17.5 Fake-data simulation as a way of life
  • 18 Simulation
    • 18.1 Simulation of discrete probability models
      • 18.1.1 How many girls in 400 births?
      • 18.1.2 Accounting for twins
    • 18.2 Simulation of continuous and mixed discrete/continuous models
      • 18.2.1 Simulation in R using custom-made functions
    • 18.3 Summarizing a set of simulations using median and median absolute deviation
    • 18.4 Bootstrapping to simulate a sampling distribution
      • 18.4.1 Choices in defining the bootstrap distribution
      • 18.4.2 Limitations of bootstrapping
    • 18.5 Fake-data simulation as a way of life
  • 19 Simulation
    • 19.1 Simulation of discrete probability models
      • 19.1.1 How many girls in 400 births?
      • 19.1.2 Accounting for twins
    • 19.2 Simulation of continuous and mixed discrete/continuous models
      • 19.2.1 Simulation in R using custom-made functions
    • 19.3 Summarizing a set of simulations using median and median absolute deviation
    • 19.4 Bootstrapping to simulate a sampling distribution
      • 19.4.1 Choices in defining the bootstrap distribution
      • 19.4.2 Limitations of bootstrapping
    • 19.5 Fake-data simulation as a way of life
  • 20 Simulation
    • 20.1 Simulation of discrete probability models
      • 20.1.1 How many girls in 400 births?
      • 20.1.2 Accounting for twins
    • 20.2 Simulation of continuous and mixed discrete/continuous models
      • 20.2.1 Simulation in R using custom-made functions
    • 20.3 Summarizing a set of simulations using median and median absolute deviation
    • 20.4 Bootstrapping to simulate a sampling distribution
      • 20.4.1 Choices in defining the bootstrap distribution
      • 20.4.2 Limitations of bootstrapping
    • 20.5 Fake-data simulation as a way of life
  • 21 Simulation
    • 21.1 Simulation of discrete probability models
      • 21.1.1 How many girls in 400 births?
      • 21.1.2 Accounting for twins
    • 21.2 Simulation of continuous and mixed discrete/continuous models
      • 21.2.1 Simulation in R using custom-made functions
    • 21.3 Summarizing a set of simulations using median and median absolute deviation
    • 21.4 Bootstrapping to simulate a sampling distribution
      • 21.4.1 Choices in defining the bootstrap distribution
      • 21.4.2 Limitations of bootstrapping
    • 21.5 Fake-data simulation as a way of life
  • 22 Simulation
    • 22.1 Simulation of discrete probability models
      • 22.1.1 How many girls in 400 births?
      • 22.1.2 Accounting for twins
    • 22.2 Simulation of continuous and mixed discrete/continuous models
      • 22.2.1 Simulation in R using custom-made functions
    • 22.3 Summarizing a set of simulations using median and median absolute deviation
    • 22.4 Bootstrapping to simulate a sampling distribution
      • 22.4.1 Choices in defining the bootstrap distribution
      • 22.4.2 Limitations of bootstrapping
    • 22.5 Fake-data simulation as a way of life
  • 23 Exercises of Regression and Other Stories
    • 23.1 Overview
      • 23.1.1 From design to decision
      • 23.1.2 Sketching a regression model and data
      • 23.1.3 Goals of regression
      • 23.1.4 Problems of statistics
      • 23.1.5 Goals of regression
    • 23.2 Causal inference
    • 23.3 Statistics as generalization
    • 23.4 Statistics as generalization
    • 23.5 A problem with linear models
      • 23.5.1 Working through your own example
    • 23.6 Some basic methods in mathematics and probability
      • 23.6.1 Weighted averages
      • 23.6.2 Weighted averages
      • 23.6.3 Probability distributions
      • 23.6.4 Probability distributions
      • 23.6.5 Probability distributions
      • 23.6.6 Linear transformations
      • 23.6.7 Linear transformations
      • 23.6.8 Correlated random variables
      • 23.6.9 Comparison of distributions
      • 23.6.10 Working through your own example
  • References
  • Published with bookdown

Reading Notes for Regression and Other Stories

Chapter 23 Exercises of Regression and Other Stories

23.1 Overview

Data for examples and assignments in this and other chapters are at www.stat.columbia.edu/~gelman/regression/. See Appendix A for an introduction to R, the software you will use for computing.

23.1.1 From design to decision

Figure 1.9 displays the prototype for a paper “helicopter.” The goal of this assignment is to design a helicopter that takes as long as possible to reach the floor when dropped from a fixed height, for example 8 feet. The helicopters are restricted to have the general form shown in the sketch. No additional folds, creases, or perforations are allowed. The wing length and the wing width of the helicopter are the only two design parameters, that is, the only two aspects of the helicopter that can be changed. The body width and length must remain the same for all helicopters. A metal paper clip is attached to the bottom of the helicopter. Here are some comments from previous students who were given this assignment:

Rich creased the wings too much and the helicopters dropped like a rock, turned upside down, turned sideways, etc. Helis seem to react very positively to added length. Too much width seems to make the helis unstable. They flip-flop during flight. Andy proposes to use an index card to make a template for folding the base into thirds. After practicing, we decided to switch jobs. It worked better with Yee timing and John dropping. 3 – 2 – 1 – GO.

Your instructor will hand out 25 half-sheets of paper and 2 paper clips to each group of students. The body width will be one-third of the width of the sheets, so the wing width can be anywhere from \(\frac{1}{6}\) to \(\frac{1}{2}\) of the body width; see Figure 1.9a. The body length will be specified by the instructor. For example, if the sheets are U.S.-sized (\(8.5\times5.5\) inches) and the body length is set to 3 inches, then the wing width could be anywhere from 0.91 to 2.75 inches and the wing length could be anywhere from 0 to 5.5 inches. In this assignment you can experiment using your 25 half-sheets and 10 paper clips. You can make each half-sheet into only one helicopter. But you are allowed to design sequentially, setting the wing width and body length for each helicopter given the data you have already recorded. Take a few measurements using each helicopter, each time dropping it from the required height and timing how long it takes to land.

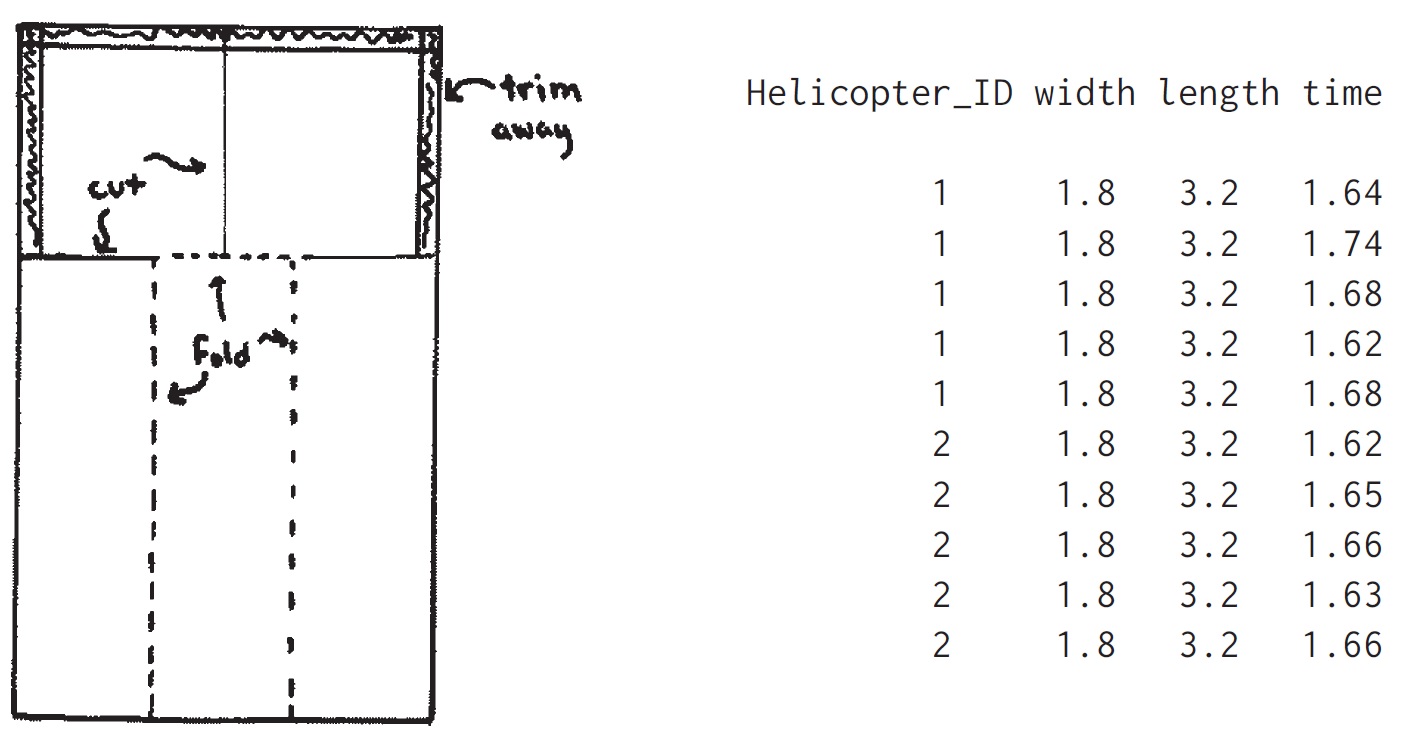
(a) Diagram for making a “helicopter” from half a sheet of paper and a paper clip. The long segments on the left and right are folded toward the middle, and the resulting long 3-ply strip is held together by a paper clip. One of the two segments at the top is folded forward and the other backward. The helicopter spins in the air when dropped. (b) Data file showing flight times, in seconds, for 5 flights each of two identical helicopters with wing width 1.8 inches and wing length 3.2 inches dropped from a height of approximately 8 feet. From Gelman and Nolan (2017).

Figure 23.1: (a) Diagram for making a “helicopter” from half a sheet of paper and a paper clip. The long segments on the left and right are folded toward the middle, and the resulting long 3-ply strip is held together by a paper clip. One of the two segments at the top is folded forward and the other backward. The helicopter spins in the air when dropped. (b) Data file showing flight times, in seconds, for 5 flights each of two identical helicopters with wing width 1.8 inches and wing length 3.2 inches dropped from a height of approximately 8 feet. From Gelman and Nolan (2017). 

library(tidyverse)
file_helicopters <- here::here("data/ros-master/Helicopters/data/helicopters.txt")
helicopters <- 
  file_helicopters %>% 
  read.table(header = TRUE) %>% 
  as_tibble(.name_repair = str_to_lower)

23.1.1.1 (a)

Record the wing width and body length for each of your 25 helicopters along with your time measurements, all in a file in which each observation is in its own row, following the pattern of helicopters.txt in the folder Helicopters, also shown in Figure 1.9b.

# The wing length and the wing width of the helicopter are the only two design variables, that is, the only two measurements on the helicopter that can be changed. The body width and length must remain the same for all helicopters. 

# wing width 4.6 centimeters and wing length 8.2 centimeters



helicopters %>% arrange(time_sec) %>% mutate(
  wing_width = c(seq(0.91, 2.75, 0.1), 2.75),
  wing_length = sample(0:5.5, 20, replace=TRUE),
  body_length = 3) %>%
  select(helicopter_id, time_sec, wing_width, 
         body_length, everything())-> helicopters
## Error in select(., helicopter_id, time_sec, wing_width, body_length, everything()): unused arguments (helicopter_id, time_sec, wing_width, body_length, everything())

23.1.1.2 (b)

Graph your data in a way that seems reasonable to you.

helicopters %>% mutate(
  helicopter_id = as.factor(helicopter_id)) %>%
  ggplot(aes(y = time_sec, x =  wing_width,
             group = helicopter_id,
             color = helicopter_id, 
             fill = helicopter_id)) + 
  geom_point() + theme_bw() + 
  theme(legend.position = "bottom")
## Error in FUN(X[[i]], ...): object 'wing_width' not found

23.1.1.3 (c)

Given your results, propose a design (wing width and length) that you think will maximize the helicopter’s expected time aloft. It is not necessary for you to fit a formal regression model here, but you should think about the general concerns of regression. The above description is adapted from Gelman and Nolan (2017, section 20.4). See Box, Hunter, and Hunter (2005) for a more advanced statistical treatment of this sort of problem.

## 
## Call:
## lm(formula = time_sec ~ width_cm + length_cm + helicopter_id, 
##     data = helicopters)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.0560 -0.0285 -0.0005  0.0175  0.0750 
## 
## Coefficients: (2 not defined because of singularities)
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.68400    0.02713  62.080   <2e-16 ***
## width_cm            NA         NA      NA       NA    
## length_cm           NA         NA      NA       NA    
## helicopter_id -0.01900    0.01716  -1.107    0.283    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.03836 on 18 degrees of freedom
## Multiple R-squared:  0.06379,    Adjusted R-squared:  0.01178 
## F-statistic: 1.227 on 1 and 18 DF,  p-value: 0.2827

23.1.2 Sketching a regression model and data

Figure 1.1b shows data corresponding to the fitted line y = 46.3 + 3.0x with residual standard deviation 3.9, and values of x ranging roughly from 0 to 4%.

23.1.2.1 (a)

Sketch hypothetical data with the same range of x but corresponding to the line \(y = 30 + 10x\) with residual standard deviation 3.9.

## 
## Call:
## lm(formula = vote_est1 ~ growth_est1, data = q1.2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -15.2023  -5.7359  -0.8188   3.8556  22.5308 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  48.4689     2.7733  17.477 6.63e-11 ***
## growth_est1   1.9846     0.6469   3.068  0.00835 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.81 on 14 degrees of freedom
## Multiple R-squared:  0.402,  Adjusted R-squared:  0.3593 
## F-statistic: 9.411 on 1 and 14 DF,  p-value: 0.00835
## Error in select(., growth_est1, growth_est2, vote_est1, vote_est2): unused arguments (growth_est1, growth_est2, vote_est1, vote_est2)

23.1.2.2 (b)

Sketch hypothetical data with the same range of x but corresponding to the line \(y = 30 + 10x\) with residual standard deviation 10.

## 
## Call:
## lm(formula = vote_est2 ~ growth_est2, data = q1.2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -25.834  -3.974   0.102   5.189  32.754 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  50.1440     3.7354  13.424 2.19e-09 ***
## growth_est2   0.3817     0.3549   1.075      0.3    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.76 on 14 degrees of freedom
## Multiple R-squared:  0.07631,    Adjusted R-squared:  0.01034 
## F-statistic: 1.157 on 1 and 14 DF,  p-value: 0.3003
## Error in select(., growth_est1, growth_est2, vote_est1, vote_est2): unused arguments (growth_est1, growth_est2, vote_est1, vote_est2)

23.1.3 Goals of regression

Download some data on a topic of interest to you. Without graphing the data or performing any statistical analysis, discuss how you might use these data to do the following things:

23.1.3.1 (a) Fit a regression to estimate a relationship of interest.

With V-Dem dataset, I will fit the model, \(\text{EDI} \sim \beta X\), which \(X\) includes various covariates that can affect the levels of democracy, which existing studies have found.

23.1.3.2 (b) Use regression to adjust for differences between treatment and control groups.

23.1.3.3 (c) Use a regression to make predictions.

23.1.4 Problems of statistics

Give examples of applied statistics problems of interest to you in which there are challenges in:

23.1.4.1 (a) Generalizing from sample to population.

23.1.4.2 (b) Generalizing from treatment to control group.

23.1.4.3 (c) Generalizing from observed measurements to the underlying constructs of interest.

23.1.5 Goals of regression

Give examples of applied statistics problems of interest to you in which the goals are:

23.1.5.1 (a) Forecasting/classification.

23.1.5.2 (b) Exploring associations.

23.1.5.3 (c) Extrapolation.

23.1.5.4 (d) Causal inference.

23.2 Causal inference

Find a real-world example of interest with a treatment group, control group, a pre-treatment predictor, and a post-treatment predictor. Make a graph like Figure 1.8 using the data from this example.

23.3 Statistics as generalization

Find a published paper on a topic of interest where you feel there has been insufficient attention to:

23.3.0.1 (a) Generalizing from sample to population.

23.3.0.2 (b) Generalizing from treatment to control group.

23.3.0.3 (c) Generalizing from observed measurements to the underlying constructs of interest.

23.4 Statistics as generalization

Find a published paper on a topic of interest where you feel the following issues have been addressed well:

23.4.0.1 (a) Generalizing from sample to population.

23.4.0.2 (b) Generalizing from treatment to control group.

23.4.0.3 (c) Generalizing from observed measurements to the underlying constructs of interest.

23.5 A problem with linear models

Consider the helicopter design experiment in Exercise 1.1. Suppose you were to construct 25 helicopters, measure their falling times, fit a linear model predicting that outcome given wing width and body length: \[ \text{time} = \beta_0 + \beta_1 ∗ \text{width} + \beta_2 ∗ \text{length}+ \text{error}, \]

and then use the fitted model \(\text{time} = \beta_0 + \beta_1 ∗ \text{width} + \beta_2 ∗ \text{length}\) to estimate the values of wing width and body length that will maximize expected time aloft.

23.5.0.1 (a) Why will this approach fail?

23.5.0.2 (b) Suggest a better model to fit that would not have this problem.

23.5.1 Working through your own example

Download or collect some data on a topic of interest of to you. You can use this example to work though the concepts and methods covered in the book, so the example should be worth your time and should have some complexity. This assignment continues throughout the book as the final exercise of each chapter. For this first exercise, discuss your applied goals in studying this example and how the data can address these goals.

23.6 Some basic methods in mathematics and probability

23.6.1 Weighted averages

A survey is conducted in a certain city regarding support for increased property taxes to fund schools. In this survey, higher taxes are supported by 50% of respondents aged 18–29, 60% of respondents aged 30–44, 40% of respondents aged 45–64, and 30% of respondents aged 65 and up. Assume there is no nonresponse.Suppose the sample includes 200 respondents aged 18–29, 250 aged 30–44, 300 aged 45–64, and 250 aged 65+. Use the weighted average formula to compute the proportion of respondents in the sample who support higher taxes.

## # A tibble: 4 x 6
##   age       support     n total weight supportweighted
##   <chr>       <dbl> <dbl> <dbl>  <dbl>           <dbl>
## 1 18-29         0.5   200  1000   0.2            0.1  
## 2 30-44         0.6   250  1000   0.25           0.15 
## 3 45-64         0.4   300  1000   0.3            0.12 
## 4 65 and up     0.3   250  1000   0.25           0.075
## # A tibble: 1 x 1
##     sum
##   <dbl>
## 1 0.445

23.6.2 Weighted averages

Continuing the previous exercise, suppose you would like to estimate the proportion of all adults in the population who support higher taxes, so you take a weighted average as in Section 3.1. Give a set of weights for the four age categories so that the estimated proportion who support higher taxes for all adults in the city is 40%.

## # A tibble: 1 x 1
##     sum
##   <dbl>
## 1 0.405

23.6.3 Probability distributions

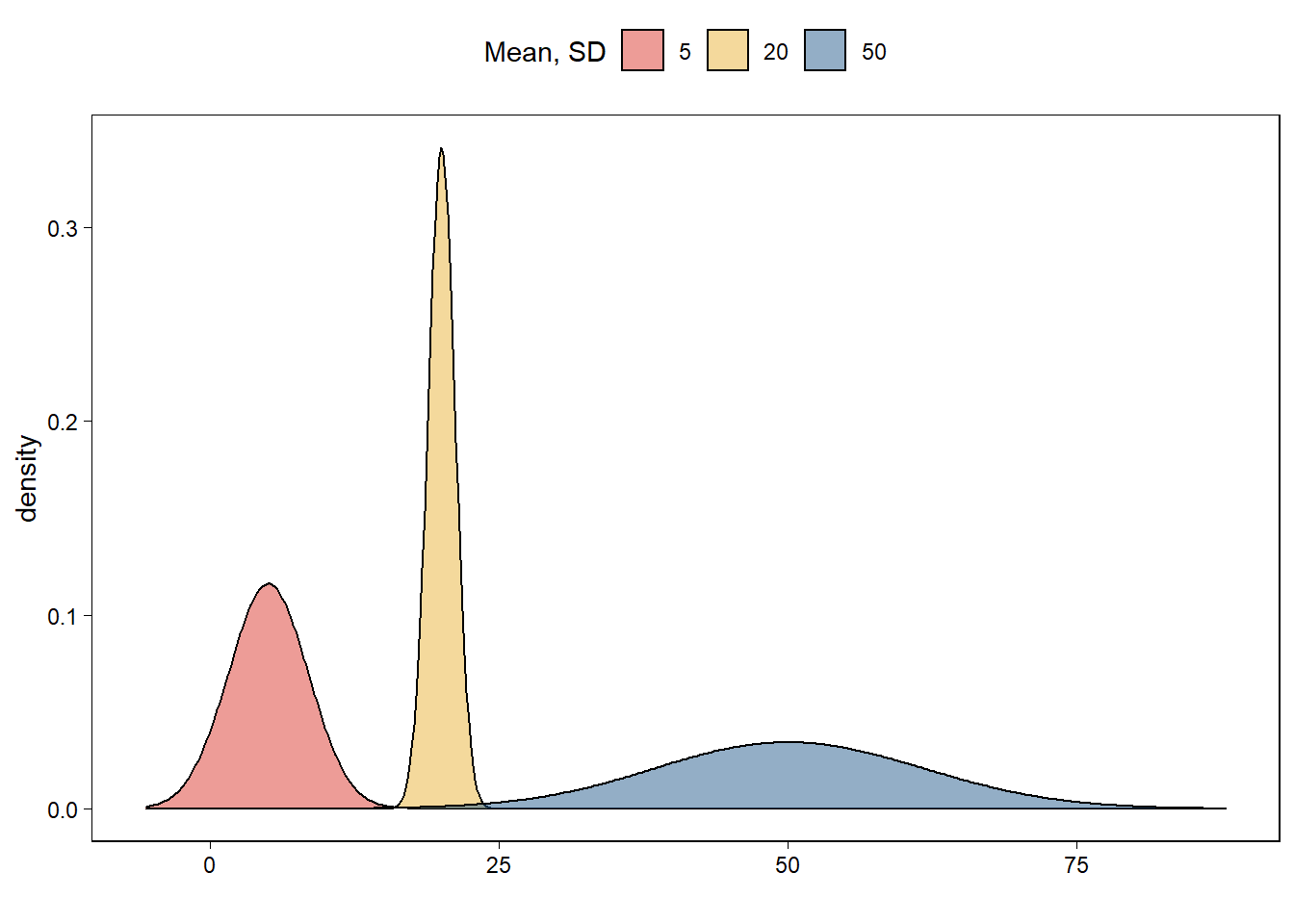
Using R, graph probability densities for the normal distribution, plotting several different curves corresponding to different choices of mean and standard deviation parameters.

23.6.4 Probability distributions

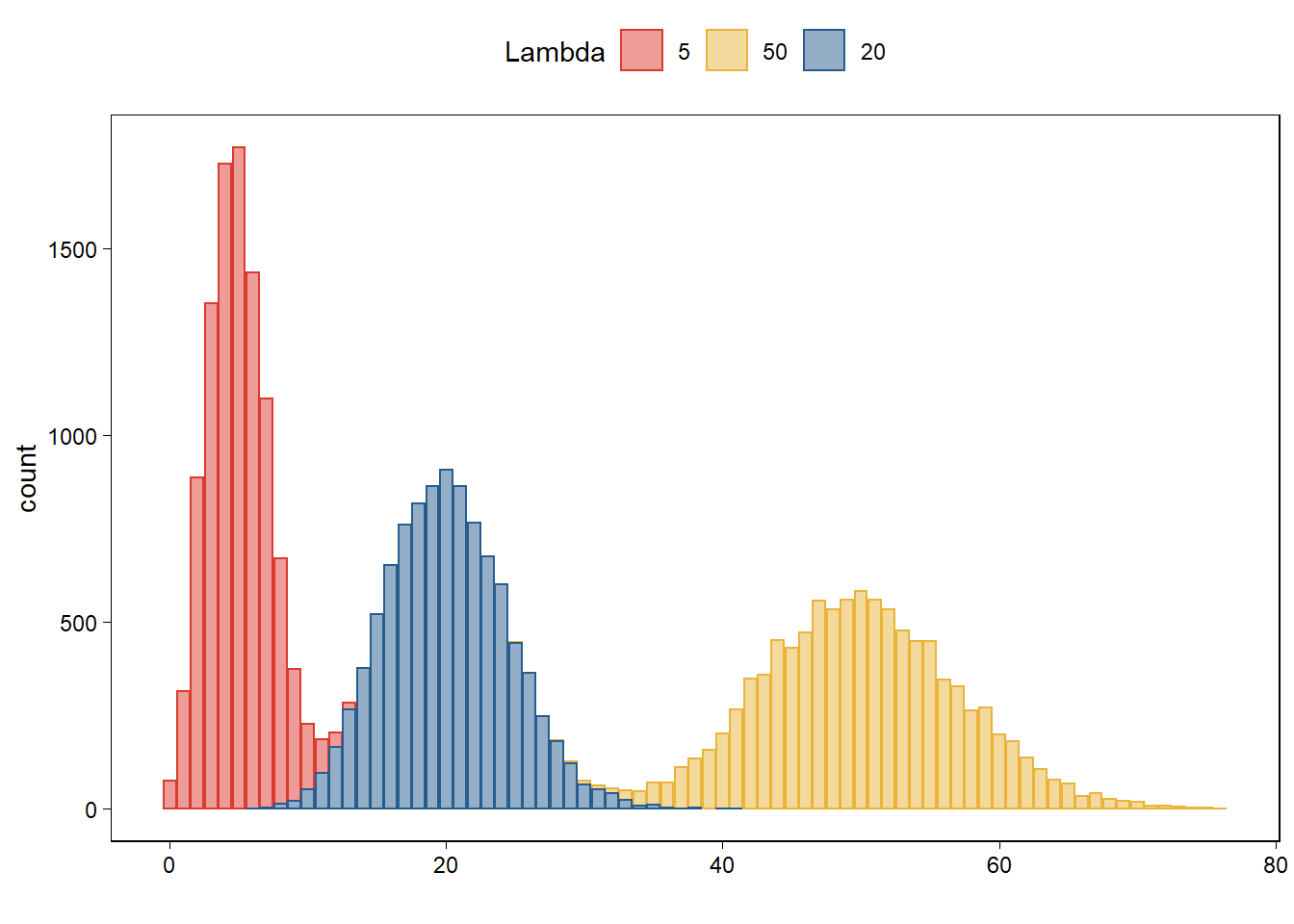
Using a bar plot in R, graph the Poisson distribution with parameter 3.5.

23.6.5 Probability distributions

Using a bar plot in R, graph the binomial distribution with n = 20 and p = 0.3.

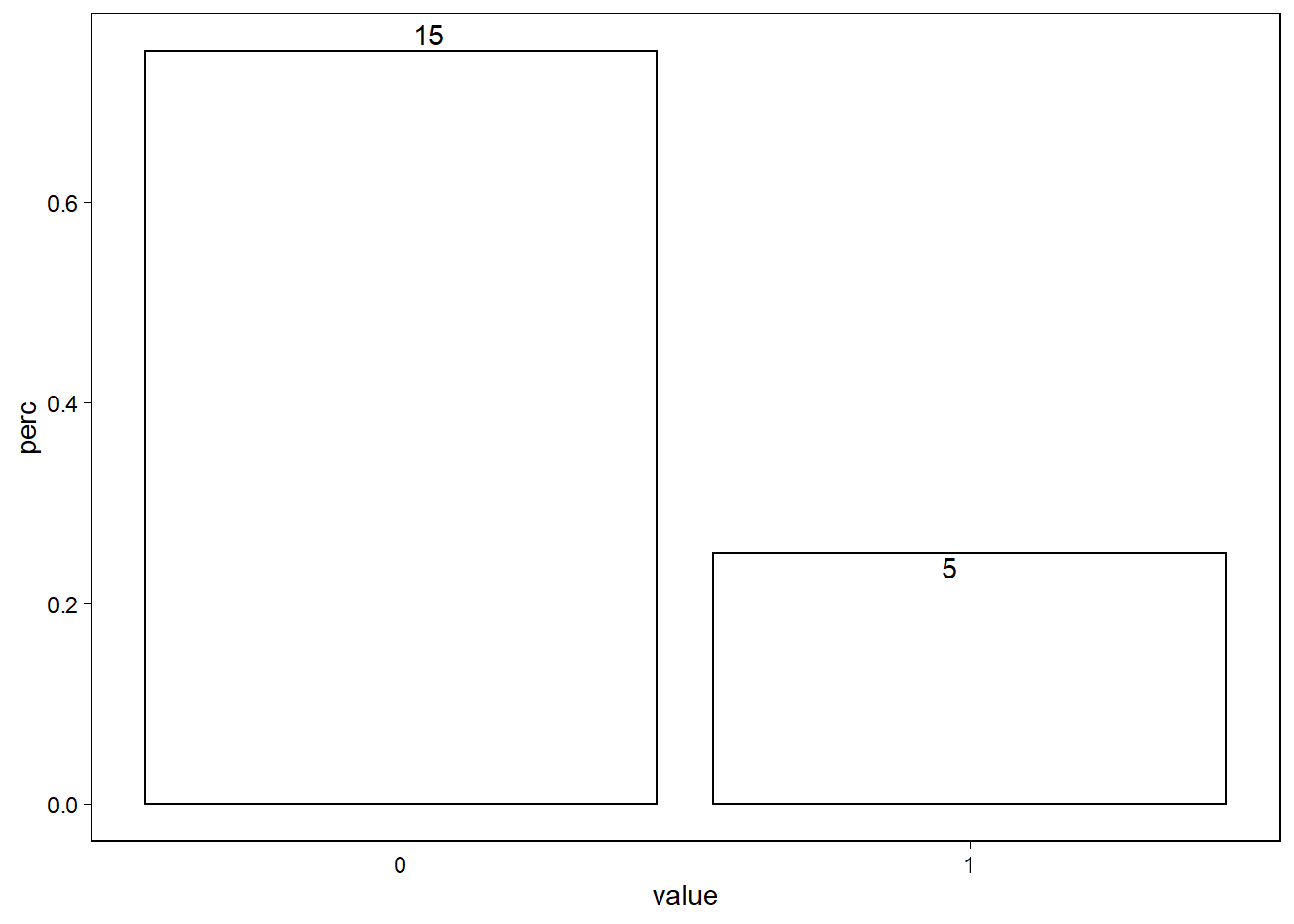
23.6.6 Linear transformations

A test is graded from 0 to 50, with an average score of 35 and a standard deviation of 10. For comparison to other tests, it would be convenient to rescale to a mean of 100 and standard deviation of 15.

23.6.6.1 (a)

Labeling the original test scores as x and the desired rescaled test score as \(y\), come up with a linear transformation, that is, values of a and b so that the rescaled scores \(y = a + bx\) have a mean of 100 and a standard deviation of 15.

23.6.6.2 (b)

What is the range of possible values of this rescaled score \(y\)?

23.6.6.3 (c)

Plot the line showing y vs. x.

23.6.7 Linear transformations

Continuing the previous exercise, there is another linear transformation that also rescales the scores to have mean 100 and standard deviation 15. What is it, and why would you not want to use it for this purpose?

23.6.8 Correlated random variables

Suppose that the heights of husbands and wives have a correlation of 0.3, husbands’ heights have a distribution with mean 69.1 and standard deviation 2.9 inches, and wives’ heights have mean 63.7 and standard deviation 2.7 inches. Let x and y be the heights of a married couple chosen at random. What are the mean and standard deviation of the average height, (x + y)/2?

23.6.9 Comparison of distributions

Find an example in the scientific literature of the effect of treatment on some continuous outcome, and make a graph similar to Figure 3.9 showing the estimated population shift in the potential outcomes under a constant treatment effect.

23.6.10 Working through your own example

Continuing the example from Exercises 1.10 and 2.10, consider a deterministic model on the linear or logarithmic scale that would arise in this topic. Graph the model and discuss its relevance to your problem.