Probabilities, Distribution, and Hypotheses
Probability into R
패키지 불러오기
library(knitr)
library(kableExtra)
library(ggplot2)
library(patchwork)
library(tidyverse)
# install.packages("devtools")
# devtools::install_github("JoeyStanley/futurevisions")
library(futurevisions)
theme_set(theme_bw())확률 관련 포스팅에서는 몇 가지 간단한 확률을 R을 통해서 증명하고(Some simple probability demonstrations), 정규분포(normal distributions)와 이항분포(binomial distributions)로부터 분위(quantiles)를 얻어내는 방법을 살펴보고자 합니다.
여기서는 일단 간단하게 정규분포랑 이항분포, 그리고 독립사건과 종속사건만 간단하게 살펴보겠습니다.
- 분위(Quantiles)에 대해 어떻게 설명할까 고민을 좀 했는데 좋은 블로그 포스팅을 찾아서 참조용으로 링크하겠습니다.
- 링크는 여기를 보시면 됩니다. Q-Q Plot 설명하면서 Quantile의 정의도 잘 정리해놓으셨습니다.
확률이란?
확률모델은 우리가 어떠한 이론-모델을 가지고 있을 때, 어떠한 데이터를 관측할 확률에 대해 알려줍니다. 동전 던지기를 예로 들어보겠습니다. 동전 던지기를 할 때, 우리는 앞면을 관측할 확률에 대해서 대강 알고 있습니다. 누구든지 물어보면 0.5의 확률이라고 말할 것입니다. 동전을 던졌을 때, 얻을 수 있는 가능성이 앞면과 뒷면이라는 두 가지밖에 없고 이 동전에 아무런 문제가 없을 때, 그 기대값이 0.5일 것이라는 일종의 이론, 모델을 가지고 있기 때문입니다. 정확히는 동전을 반복해서 던졌을 때(=관측이 반복될 때) 데이터가 어떻게 나타날 것(앞면 뒷면이 반반)이라는 자료생성과정에 관한 이론을 우리가 가지고 있다는 것입니다. 우리가 어떤 모델, 이론을 가지고 있을 때, \(Y\)라는 결과를 얻을 확률을 아래와 같이 적어보겠습니다.
\[ \Pr(Y|M) = \Pr(\text{데이터}|\text{모델}) \]
다음으로는 확률의 종류에 대해서 알아보도록 하겠습니다. 예전에 배우셨던 집합 개념을 조금 떠올리실 필요가 있습니다. 먼저, 사건 A와 사건 B가 있다고 하겠습니다. 그리고 이 두 사건이 동시에 일어날 확률을 A와 B에 대한 결합확률(joint probability)이라고 하겠습니다. 집합 기호로 나타내면 \(\Pr(A\cap B)\)로 나타낼 수 있으며, \(\Pr(A\;\text{and}\;B)\)라고도 합니다.
한계확률은 전체 중에서 특정 사건이 발생할 확률을 말합니다. 예를 들어서, 아래와 같은 상황이 있다고 하겠습니다. A라는 국가와 B라는 국가가 서로 갈등하는 국면에 놓여있는 상황입니다. A와 B 모두가 싸우기로 결정할 확률은 \(\Pr(A_{\text{Fight}}\;\cap\;B_{\text{Fight}}) = 0.3\)이라고 할 수 있습니다. 반대로 두 국가 모두가 서로 싸움을 회피하고 상대방의 요구에 순응할 확률은 \(\Pr(A_{\text{Comply}}\;\cap\;B_{\text{Comply}}) = 0.4\)입니다. 이 두 경우 모두 결합확률이죠. 그렇다면 A가 싸울 한계확률은 얼마일까요? 전체 중에 \(A_{\text{Fight}}\)일 경우이므로 0.4라고 할 수 있습니다. 마찬가지로 \(\Pr(A_{\text{Comply}}) = 0.6\)이며, 같은 논리로 \(\Pr(B_{\text{Fight}}, B_{\text{Comply}})\)는 각각 0.5, 0.5 라고 할 수 있습니다.
| 구분 | A\(_{\text{Fight}}\) | A\(_{\text{Comply}}\) | 총합 |
|---|---|---|---|
| B\(_{\text{Fight}}\) | 0.3 | 0.2 | 0.5 |
| B\(_{\text{Comply}}\) | 0.1 | 0.4 | 0.5 |
| 총합 | 0.4 | 0.6 | 1 |
그럼 위의 표를 바탕으로 조건부확률(conditional probability)도 한 번 살펴보겠습니다. 조건부확률이란 한계확률 대비 결합확률의 비율이라고 할 수 있습니다. A와 B라는 사건으로 일반화된 진술로 표현하자면, \(\Pr(A|B) = \Pr(A \cap B)/\Pr(B)\)라고 할 수 있으며, 이때 조건부확률은 사건 B 일어났을 경우에 A라는 사건이 나타날 확률을 의미합니다.
하나 더 살펴보도록 하겠습니다. 유권자들에게 A라는 후보에게 투표했는지, 혹은 B라는 후보에게 투표했는지 묻고, 동시에 그들이 남성인지 여성인지에 대해 물었다고 해보겠습니다.
| 구분 | A | B | 총합 |
|---|---|---|---|
| 남성 | 40 | 60 | 100 |
| 여성 | 65 | 35 | 100 |
| 총합 | 105 | 95 | 200 |
이때, 한계확률과 조건부확률, 그리고 결합확률을 각각 살펴보겠습니다.
먼저 응답자가 여성일 한계확률은 전체 200명 중에 여성 100명이므로 \(\Pr(\text{female}) = 100/200 = 0.5\)라고 할 수 있습니다.
그렇다면 이 여성 중에서
A후보에게 투표했을 조건부확률은 전체 여성 100명 중A후보에게 투표한 65명, 즉 \(\Pr(\text{A}|\text{female}) = 65/100 = 0.65\)입니다.그렇다면
A후보에 투표했으면서 동시에 여성일 확률은 어떻게 될까요? 일단 이 두 사건이 독립적이라는 가정 하에서 우리는 이 두 사건의 확률을 곱해주면 됩니다. 즉, \(\Pr(\text{A}, \text{female}) = \Pr(\text{A})\;\;\text{AND}\;\;\Pr(\text{female}) = 65/200 = 0.325\)라는 얘기입니다.
조건부확률은 한계확률에 대한 결합확률의 비율이라고 이해할 수 있습니다:
\(\Pr(A|B) = \Pr(A, \;B)/\Pr(B)\)
\(\Pr(\text{A}|\text{female}) = \Pr(\text{A}, \;\;\text{female})/\Pr(\text{female})\)
\(\Pr(\text{A}|\text{female})/\Pr(\text{female}) = 0.325/0.5 = 0.65\)
결합확률, 한계확률, 그리고 조건부확률은 앞으로를 개념들을 이해하는 데 중요하니까 머리에 잘 담아두시고, 이제 다음으로 넘어가겠습니다.
주사위굴리기 게임!
확률을 공부할 때, 지겹도록 등장하는 놈들이 총 셋이 있습니다. 동전, 카드, 그리고 주사위입니다. 인류는 아마도 이 셋을 만듦으로써 스스로를 괴롭히는 통계학을 발전시켰는지도 모르겠습니다… 일단 주사위 굴리기는 직관적으로 확률과 통계를 이해하기 좋은 방식입니다. 먼저 주사위 하나를 한 번 굴리는 것을 시뮬레이팅하는 함수를 코딩해보겠습니다.
die <- as.integer(runif(1, min=1, max=7))
die[1] 2die는 ?runif 라고 입력하여 살펴보면 generates random deviates.라고 기술되어 있는 것을 확인할 수 있습니다. 이어지는 함수를 풀어서 설명하면 다음과 같습니다: > 다음의 결과를 정수의 형태로 저장하라(as.integer) \(\rightarrow\) 무작위로 다음의 범주 내에서 다른 값을 1번 추출하라 \(\rightarrow\) 최소값은 1, 최대값은 6 (1 이상 7미만)을 갖게하라.
그러면 이번에는 두 개의 주사위를 굴려보도록 하겠습니다. 굴리는 횟수는 한 번입니다.
dice <- (as.integer(runif(1, min=1, max=7))) +
(as.integer(runif(1, min=1, max=7)))
dice[1] 9여기서 + 연산자는 부울리안 논리에 따르면 OR를 의미합니다. 즉 각 주사위를 한 번씩 랜덤으로 굴려 얻는 값을 더한 결과를 dice에 저장하라는 명령입니다. 그럼 이번에는 100번, 1000번, 그리고 100만번을 돌려겠습니다.
# Draw 100 times of two dice
dice100 <- (as.integer(runif(100, min=1, max=7))) +
(as.integer(runif(100, min=1, max=7)))
dice100 %>% table() %>% kable(col.names = c("Dice", "Freq"))| Dice | Freq |
|---|---|
| 2 | 4 |
| 3 | 4 |
| 4 | 11 |
| 5 | 12 |
| 6 | 9 |
| 7 | 21 |
| 8 | 12 |
| 9 | 10 |
| 10 | 8 |
| 11 | 6 |
| 12 | 3 |
# Draw 1000 times of two dice
dice1000 <- (as.integer(runif(1000, min=1, max=7))) +
(as.integer(runif(1000, min=1, max=7)))
dice1000 %>% table() %>% kable(col.names = c("Dice", "Freq"))| Dice | Freq |
|---|---|
| 2 | 19 |
| 3 | 50 |
| 4 | 78 |
| 5 | 89 |
| 6 | 151 |
| 7 | 178 |
| 8 | 145 |
| 9 | 116 |
| 10 | 83 |
| 11 | 62 |
| 12 | 29 |
# Draw 1 milion times of two dice
dice10000 <- (as.integer(runif(1e4, min=1, max=7))) +
(as.integer(runif(1e4, min=1, max=7)))
dice10000 %>% table() %>% kable(col.names = c("Dice", "Freq"))| Dice | Freq |
|---|---|
| 2 | 292 |
| 3 | 531 |
| 4 | 847 |
| 5 | 1055 |
| 6 | 1357 |
| 7 | 1658 |
| 8 | 1379 |
| 9 | 1144 |
| 10 | 881 |
| 11 | 571 |
| 12 | 285 |
이렇게 시뮬레이팅한 세 결과를 히스토그램으로 살펴보겠습니다.
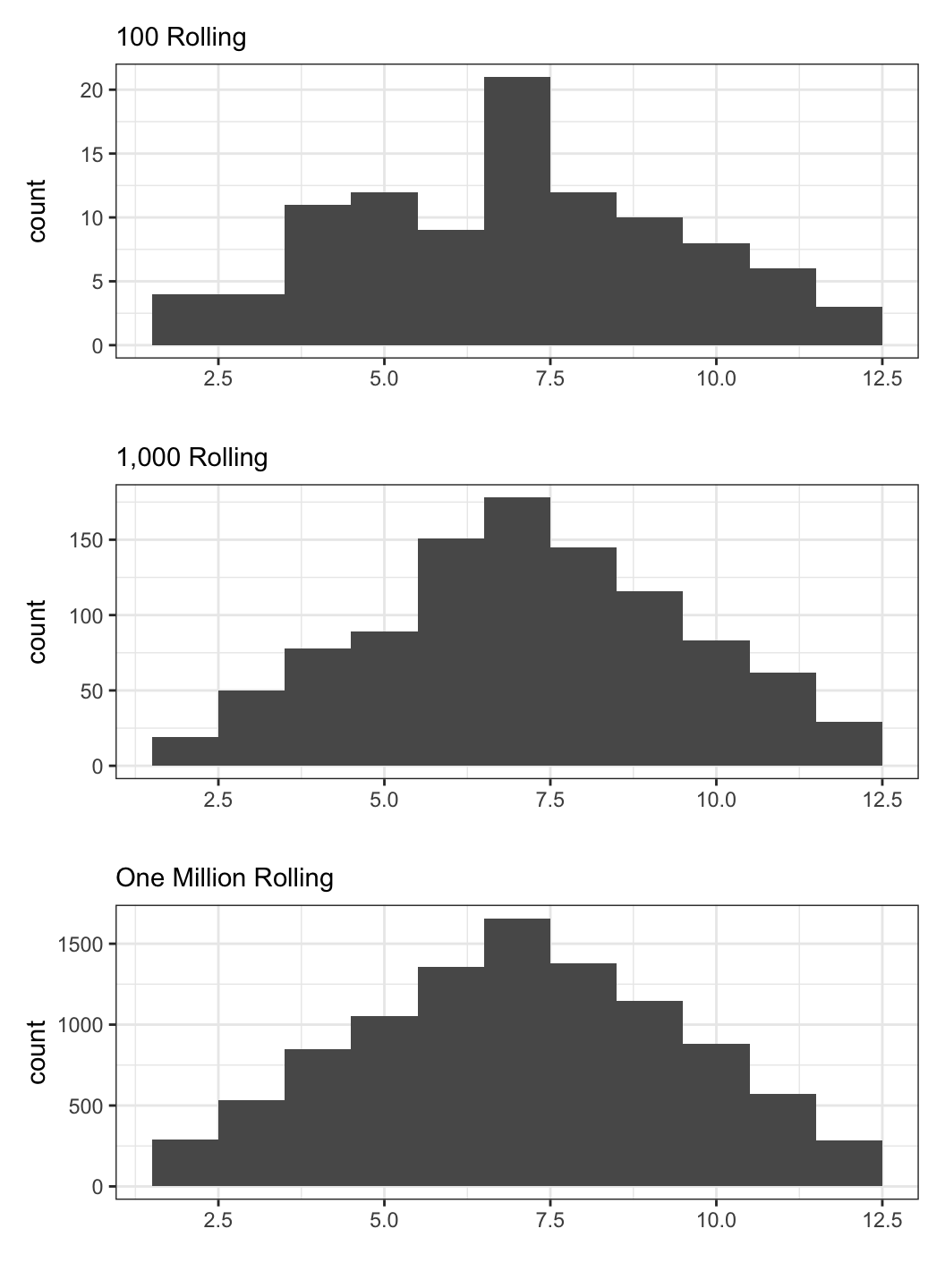
일단 가시적으로 살펴볼 수 있게 각 코드 이후에 그 결과값의 빈도를 표로 나타내보았습니다. 그리고 그 표를 히스토그램으로 재구성해보았습니다. 역시 N이 늘어날 수록 우리(?)가 사랑하는 그 녀석의 모습이 드러나기 시작합니다.
주사위는 1에서 6까지의 한정된 값을 가지고, 두 개를 합쳐서 굴려봐야 2부터 12까지의 한정된(bounded) 값이긴 하지만 이 주사위 굴리기를 통해서 우리는 지난 번 포스팅에서 살펴보았던 것처럼 정규분포(normal distribution)와 표본 크기(n), 혹은 표집(sampling)의 관계를 간접적으로 다시 한 번 살펴볼 수 있습니다.
동전 던지기
그럼 이번에는 동전을 한 번 던져보겠습니다. 저는 아직까지 앞면 뒷면 이외에 옆면에도 표기를 지닌 동전을 본 적이 없으니, 여기서의 동전도 앞면과 뒷면이라는 두 개의 값만을 가진다고 가정하겠습니다. 삼면이나 사면을 가진 동전을 보신 분들은 부디 댓글로 알려주시길… 나와라 검은 백조야(김웅진 · 김지희 2012, p.53).
아무튼 앞면과 뒷면이 있는 경우에 그 각각이 나올 확률은 0.5, 0.5라고 할 수 있습니다. rbinom()은, randomly [drawn] binomial, 무작위로 이항변수를 추출하라는 함수라고 할 수 있습니다. 백문이 불여일코드.
coin <- rbinom(5, 1, .5)
coin[1] 1 1 1 0 0이어지는 함수를 풀어서 설명하면 다음과 같습니다.: 이항변수로 무작위로 추출하라(rbinom()) \(\rightarrow\) 5번 추출하라 \(\rightarrow\) 최대값은 1 (=최소값은 0) \(\rightarrow\) 추출확률은 0.5. 즉, 1이 나올 확률을 50%로 설정하여 무작위로 추출하라는 것입니다. 그럼 이번에는 100개의 동전을 던져보겠습니다.
# Draw a coin 100 times
coin100 <- rbinom(100, 1, .5)
coin100 %>% table() %>% kable(col.names = c("Coin", "Freq"))| Coin | Freq |
|---|---|
| 0 | 51 |
| 1 | 49 |
# Draw a coin 1000 times
coin1000 <- rbinom(1000, 1, .5)
coin1000 %>% table() %>% kable(col.names = c("Coin", "Freq"))| Coin | Freq |
|---|---|
| 0 | 476 |
| 1 | 524 |
# Draw a coin 1 milion times
coin10000 <- rbinom(10000, 1, .5)
coin10000 %>% table() %>% kable(col.names = c("Coin", "Freq"))| Coin | Freq |
|---|---|
| 0 | 5077 |
| 1 | 4923 |
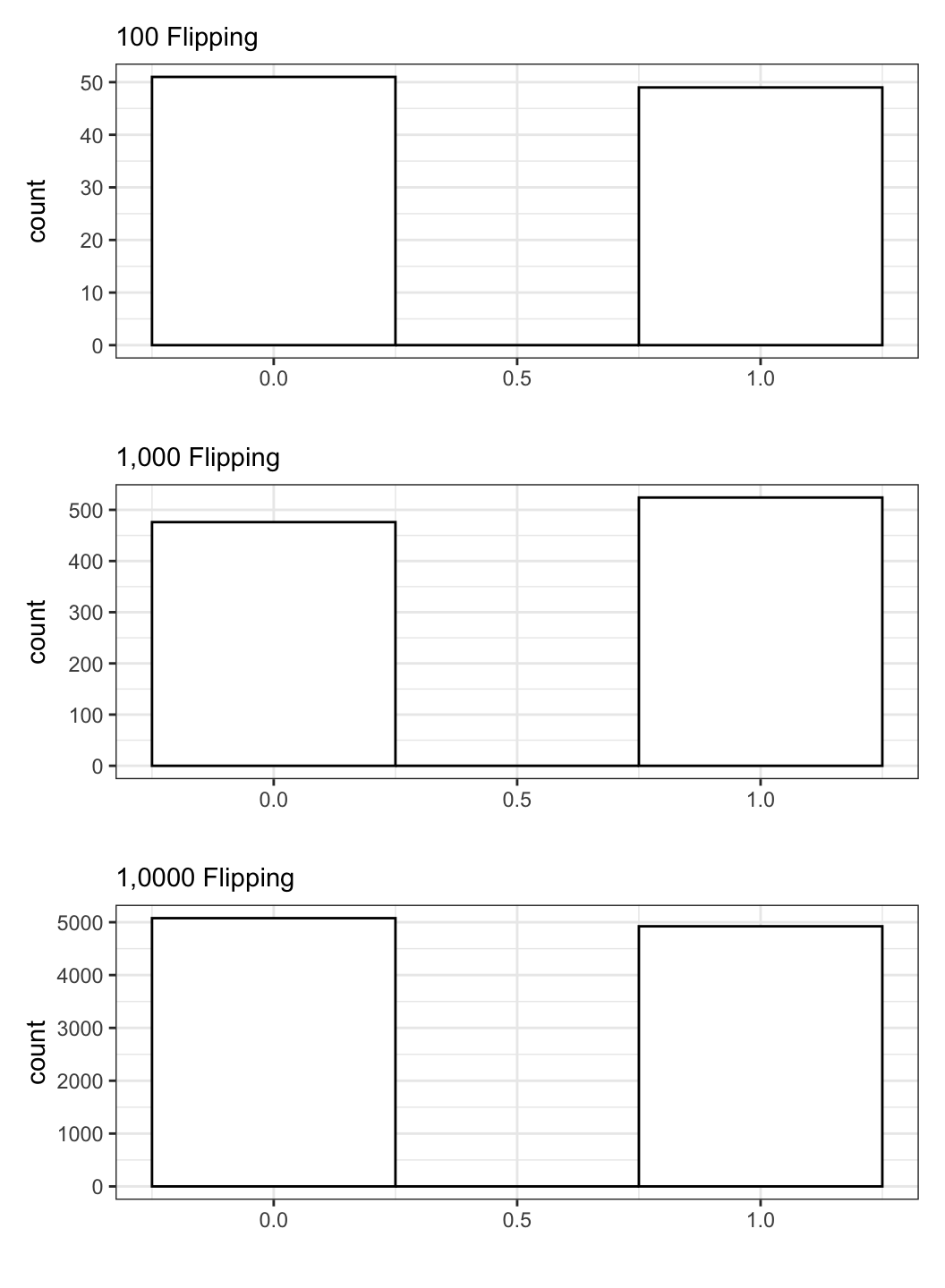
이와 같이 이항변수는 나뉘어진(discrete) 값을 가집니다. 히스토그램으로 그리면 0이 나오는 빈도랑 1이 나오는 빈도만 보여주는 것이지요. 이번에는 100개의 동전을 1000번 던지는 경우를 시뮬레이팅해보겠습니다.
coin1Mx <- rep(NA, 1e6)
for (i in 1:1e6) {
coin1Mx[i] <- sum(rbinom(100, 1, .5))
}
coin1Mx %>% as_tibble() %>%
ggplot(aes(value)) +
geom_histogram(aes(y = ..density..),
color = "black", fill = "white") +
labs(x = "Number of heads") +
theme_bw()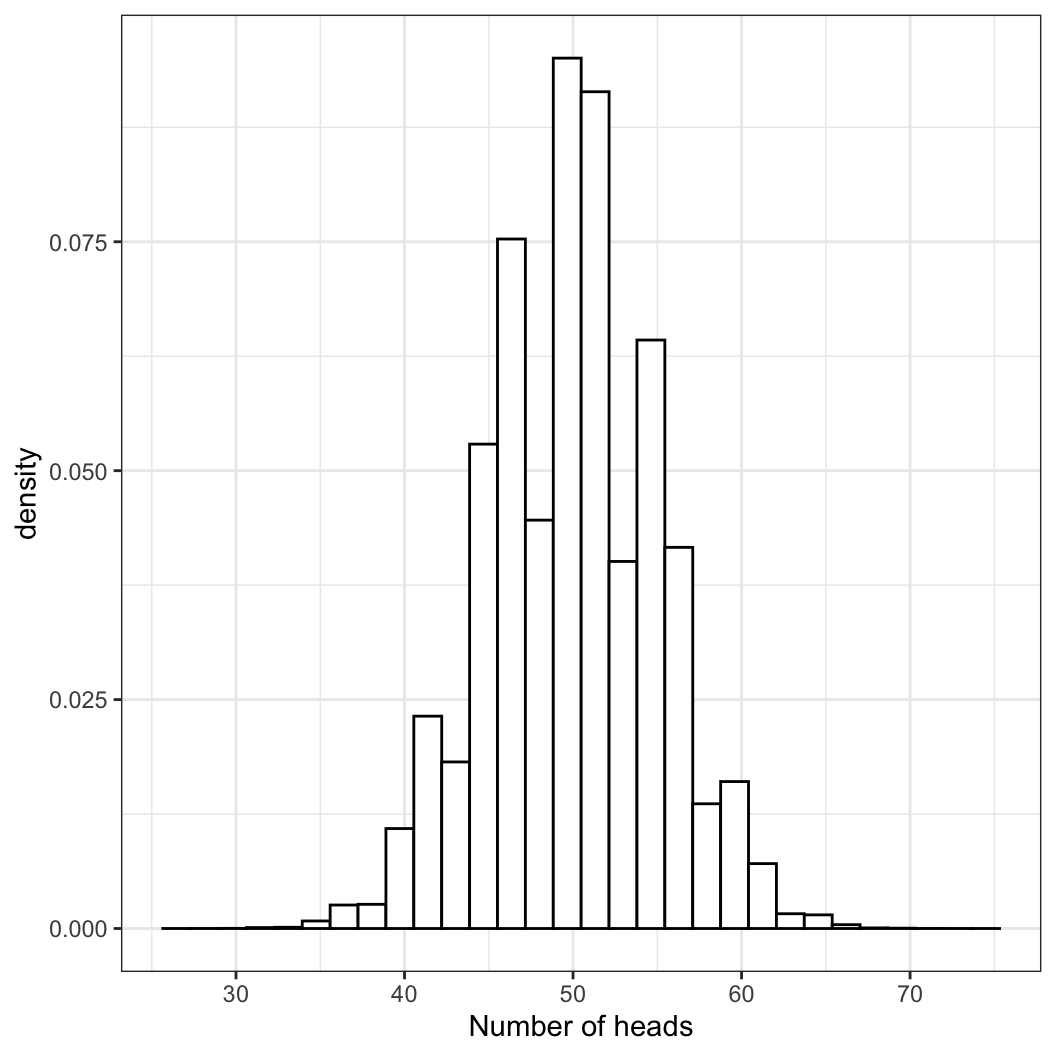
100만 개의 셀을 결측치(NA)로 갖는 텅빈 coinMx라는 벡터를 만들어보겠습니다. 그리고 i가 1에서 100만까지 반복되는 loop를 구성합니다. coin1Mx_1부터 coin1Mx_1000000까지 총 100만개의 coin1Mx_n들은 모두 100개의 동전을 던져서 앞면(1)이 나오는 경우의 수를 더한 각각의 값을 가질 것입니다. 따라서 coin1Mx는 100만개의 요소를 지닌 벡터입니다.
이 자료를 활용해서 만약 100개를 던졌을 때, 앞면이 60번 나오는 것이 과연 극단적인 확률일지 아니면 무던한 것일지 확인해보겠습니다. 먼저, 60번 이상 앞면이 나온 경우를 세는 함수를 짜보겠습니다.
coin1Mx[coin1Mx > 60] %>% table() %>%
kable(col.names = c("Head > 60", "Freq."))| Head > 60 | Freq. |
|---|---|
| 61 | 7179 |
| 62 | 4551 |
| 63 | 2670 |
| 64 | 1580 |
| 65 | 883 |
| 66 | 468 |
| 67 | 221 |
| 68 | 108 |
| 69 | 45 |
| 70 | 11 |
| 71 | 8 |
| 72 | 1 |
| 73 | 3 |
| 75 | 1 |
앞면이 나오는 빈도가 61번 이상부터는 점차 감소하는 것을 확인할 수 있습니다. 그렇다면 이번에는 앞면이 60번 넘게 나올 확률을 구해보겠습니다.
먼저 앞면이 60번 넘게 나온 시뮬레이션 횟수/전체 시뮬레이션 횟수를 구합니다.
length(coin1Mx[coin1Mx > 60])/length(coin1Mx)[1] 0.017729앞면이 60번 넘게 나온 시뮬레이션 횟수를 표로 나타내서 총합을 구한 뒤 시뮬레이션 전체 횟수로 나누어 줍니다. 위와 동일합니다.
sum(table(coin1Mx[coin1Mx > 60]))/1e6[1] 0.017729length()는 count()랑 같은 개념이라고 할 수 있습니다. 전체 coin1Mx의 수, 즉 100만 건 중에서 앞면이 60번보다 많이 나온 경우의 수가 어느 정도인지를 계산한 것입니다. 즉, 앞면이 60번보다 더 많이 나올 확률은 매우 작다고 할 수 있습니다다. 앞면이 60번 초과하여 나올 확률은 “평균적” or “일반적”인 것은 아니라는 뜻입니다.
독립사건 시뮬레이션
두 개의 독립적인 사건을 시뮬레이션해보겠습니다. 첫 번째 함수는 rand1이라는 자료에 최소값 0, 최대값 10 미만의 값을 가지는 100개의 수를 무작위로 담으라는 명령입니다. 두 번째 함수는 정규분포를 따라 평균이 0이고 표준편차가 2의 값을 갖는 분포에서 100개의 값을 무작위로 추출해 rand2라는 자료에 담으라는 명령입니다.
일단 보면
rand2의 경우, 비록 명령으로 평균을 0으로 하라고 설정했지만 무작위 추출 결과 100개의 값의 평균은 0보다 약간 큰 것을 확인할 수 있습니다.이제 두 값을 각각 \(x\)축, \(y\)축으로 설정하여 100개의 값을 좌표에 매칭시킨 그래프로 나타내보겠습니다.
rand1 <- runif(100, min = 0, max = 10)
summary(rand1) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0841 2.3154 4.6746 4.8714 7.3492 9.9875 rand2 <- rnorm(100, mean = 0, sd = 2)
summary(rand2) Min. 1st Qu. Median Mean 3rd Qu. Max.
-4.44421 -1.05345 0.04528 0.32399 1.66519 5.07324 rand.dat <- tibble(rand1 = rand1,
rand2 = rand2)
rand.dat %>% ggplot(aes(x = rand1, y = rand2)) +
geom_point(alpha = 0.3, size = 2, fill = "#752021", shape = 21) +
theme_bw()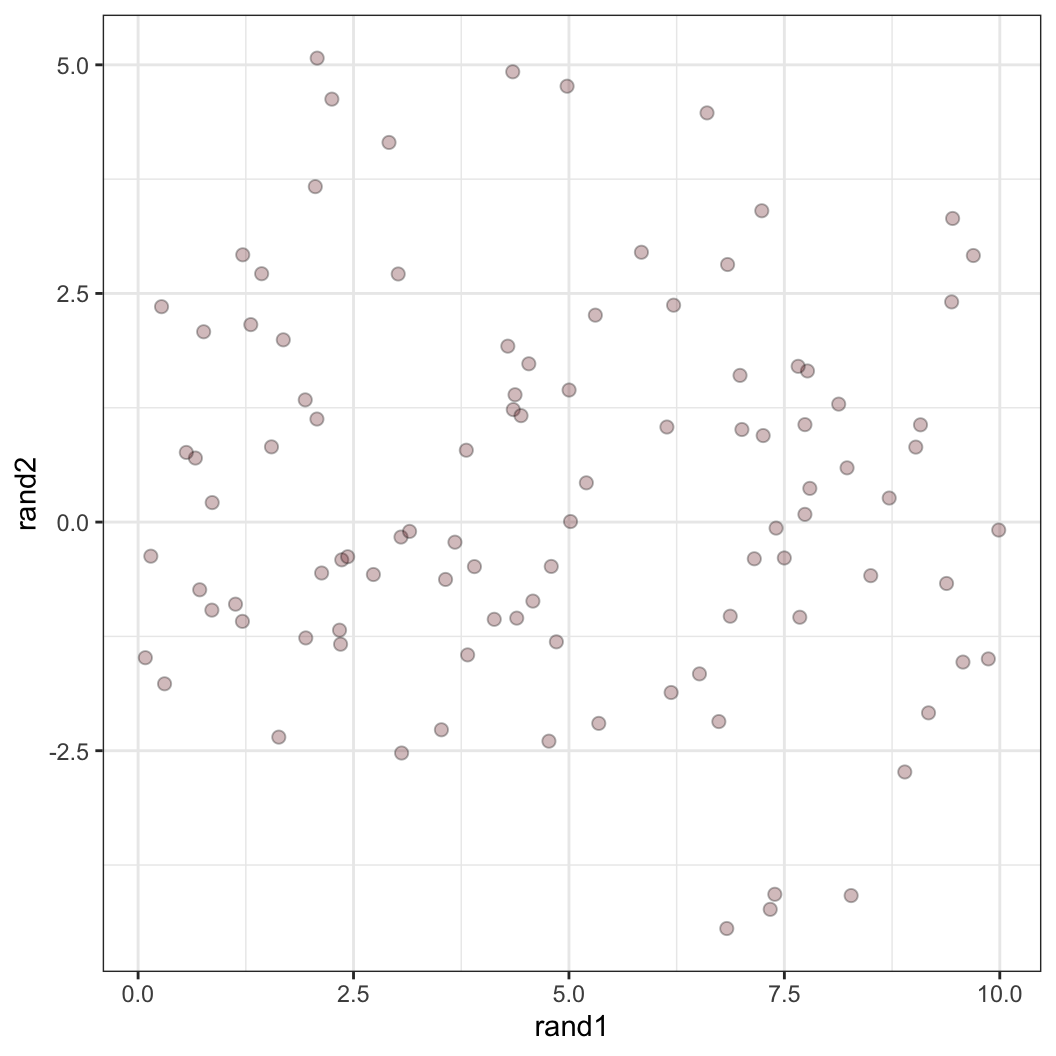
결과적으로 이 그래프에서 우리는 rand1과 rand2 간에는 어떠한 경향성을 발견하기 힘듭니다. 즉, 독립적이라는 것은 두 변수 간에 어떠한 관계를 상정할 수 없다는 것으로 이해할 수 있습니다.
종속사건 시뮬레이션
이번에는 두 사건이 종속적 관계에 있는, 즉 한 사건에서의 변화가 다른 사건에 영향을 미치는 경우를 시뮬레이션해 보겠습니다.
rand3는 아까 만들어놓은 rand1에다가 0.75를 곱해서 4를 더한 100개의 값에다가 사실 상 rand2와 같은 방식으로 구한 값을 더하여 구한 자료입니다. 즉, 이 값은 rand1의 값에 어떠한 조치를 취하여 얻은 값이므로 rand1에 영향을 받은 결과물이라고 할 수 있습니다. 이렇게 구한 rand3와 rand1 간의 관계를 그래프로 나타내봅시다.
rand.dat <- rand.dat %>%
mutate(
rand3 = 4 + 0.75 * rand1 + rnorm(100, mean = 0, sd = 2)
)
rand.dat %>% ggplot(aes(x = rand1, y = rand3)) +
geom_point(alpha = 0.3, size = 2, fill = "#752021", shape = 21) +
theme_bw()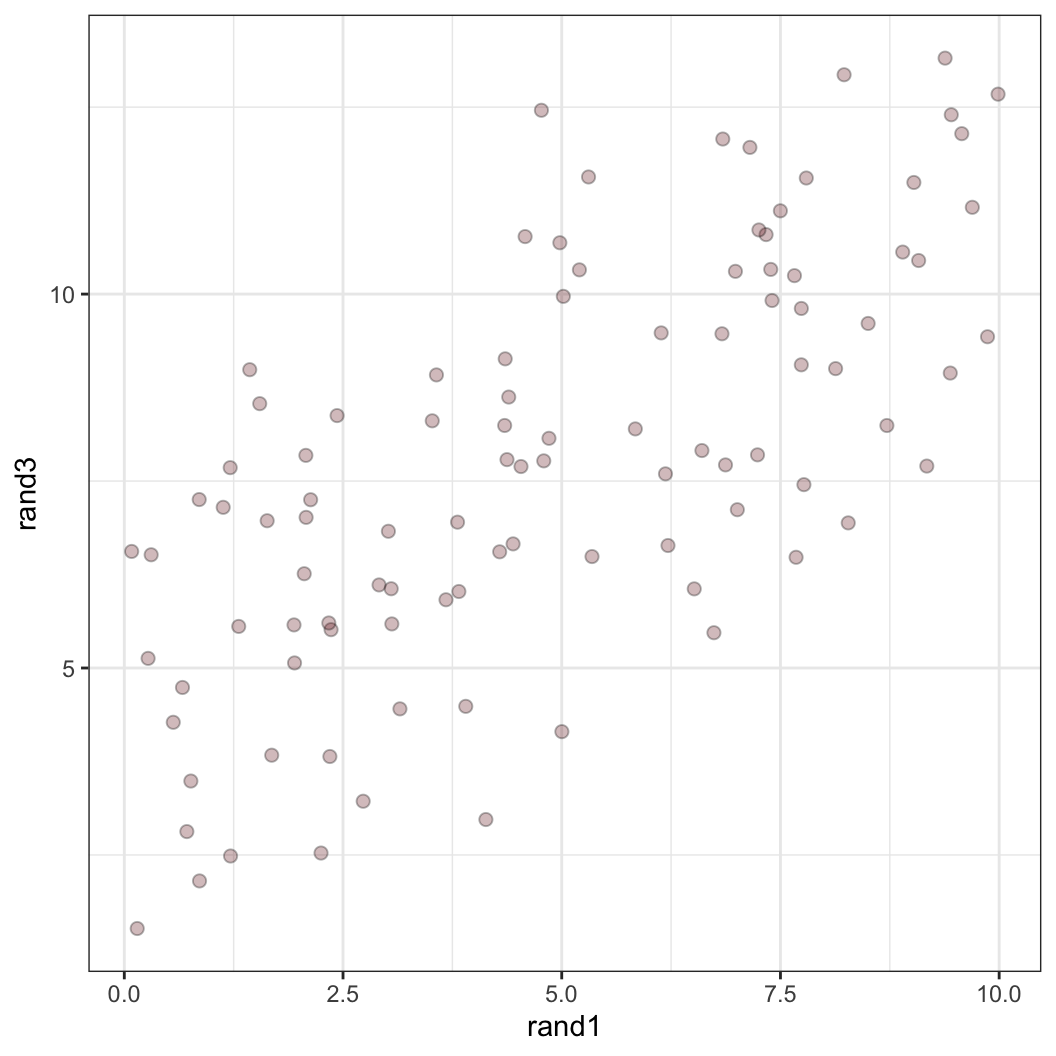
이 그래프의 해석은 나중에 산포도(scatter plot) 및 단순회귀분석(simple regression)을 살펴볼 때 다시 한 번 다룰 것입니다. 일단 여기서는 rand1이 증가할 때, rand3도 증가세를 보이는—둘의 인과적 관계는 확인할 수 없지만 아무튼—양(positive)의 관계를 보이고 있다는 것을 알 수 있습니다.
cor(rand1, rand3)로 두 변수 간의 상관계수를 구해보면1, 양수의 기울기를 얻게 됩니다.
이번에는 보다 더 불확실성을 가지는 종속사건의 관계를 시뮬레이션해보겠습니다. 여기서 말하는 불확실성은 더 큰 표준편차를 의미합니다.
- 표준편차가 평균에서 각 관측치가 떨어져 있는 거리의 평균이라고 할 때,
- 표준편차 값이 크다는 것은 개별 값들이 평균에서 더 넓게 분포해 있다는 것을 의미합니다.
rand.dat <- rand.dat %>%
mutate(
rand4 = 4 + 0.75 * rand1 + rnorm(100, mean = 0, sd = 5)
)
rand.dat %>% ggplot(aes(x = rand1, y = rand4)) +
geom_point(alpha = 0.3, size = 2, fill = "#752021", shape = 21) +
theme_bw()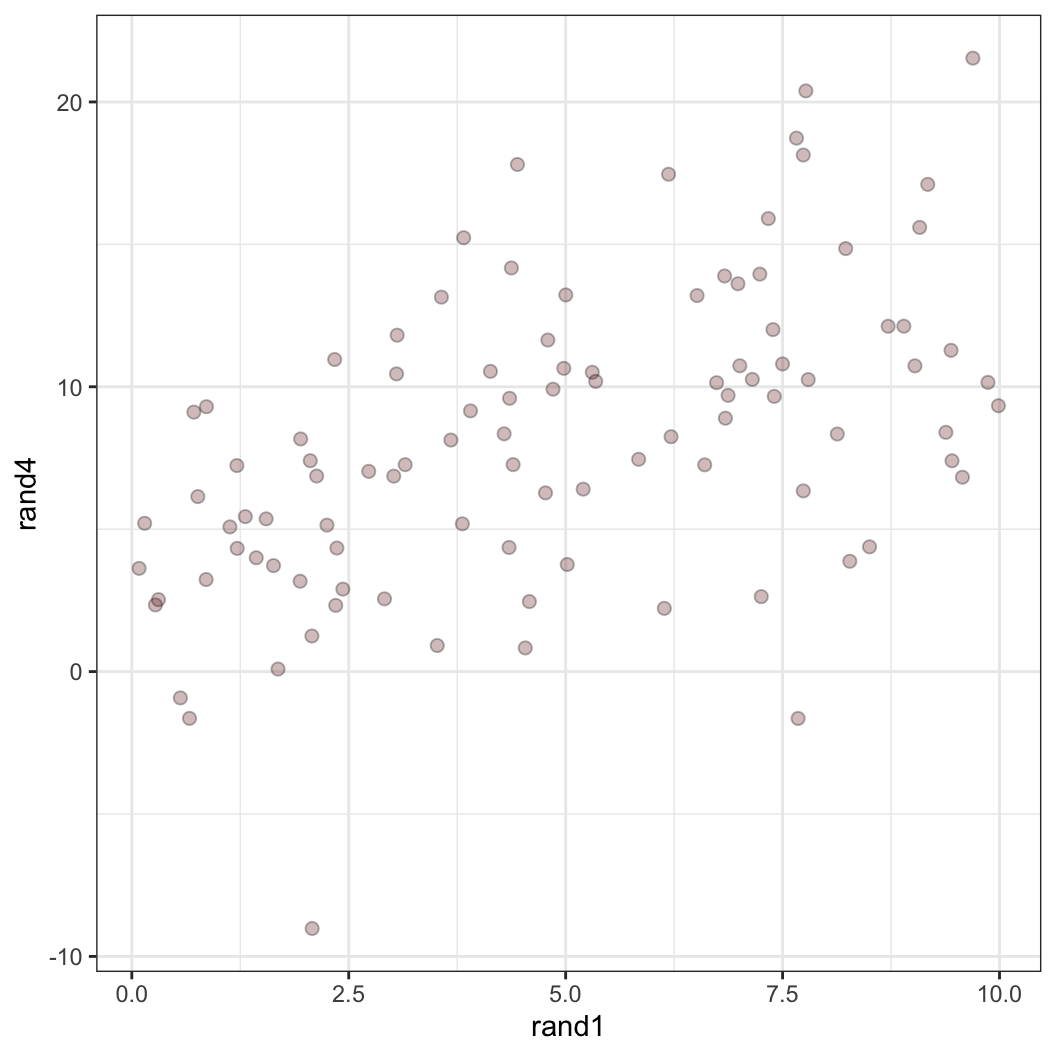
cor(rand.dat$rand1, rand.dat$rand4)[1] 0.5179773데이터 프레임을 가지고도 상관관계를 구할 수 있습니다. {corr} 패키지를 이용해보겠습니다.
## install.packages("corrr")
library(corrr)
rand.dat %>% select(rand1, rand4) %>% correlate(quiet = T) %>%
kable(col.names = c("Variables", "rand1", "rand4"), digits = 3)| Variables | rand1 | rand4 |
|---|---|---|
| rand1 | NA | 0.518 |
| rand4 | 0.518 | NA |
rand1과 rand4의 산포도는 좀 더 넓게 퍼진 모양새를 보이고 둘의 상관관계는 식에서 상정한 0.75라는 기울기보다 더 낮아지는 것을 확인할 수 있습니다.
Distribution into R
분포(Distribution)
이전 주차의 확률 파트에서 설명한 것과 같이 확률이란 “하나의 사건이 일어날 수 있는 가능성을 수치로 나타낸 것”이라고 할 수 있으며, 일반적으로 사건 A가 나타날 확률을 P(A)라고 표현합니다. 통계학에서 확률이란 일종의 경험적 확률로 한 사건 A가 일어날 확률을 P(A)라고 할 때, \(n\)번의 반복 시행에서 사건 A가 나타난 횟수를 \(r\)이라고 하면, 상대도수 \(\frac{r}{n}\)은 \(n\)이 커질수록 확률 P(A)에 가까워진다는 것을 알 수 있습니다. 즉, \(\lim r/n = P(A)\)인 경우, 이 P(A)를 사건 A의 통계적 확률이라고 합니다. 이에 기초해서 조건부 확률과 한계확률에 대한 내용을 떠올려주시면 될 것 같습니다.
그렇다면 분포란 무엇일까요? 우리가 관심을 가지고 있는 것은 바로 확률분포(probability distribution)입니다. 확률분포란 “한 번의 시행에서 변수 \(X\)가 취할 수 있는 값에 대하여 \(X\)가 취할 수 있는 값, \(x_1, x_2, x_3, \dots, x_n\)에 대응하는 확률을 \(p_1, p_2, p_3, \dots, p_n\)이라고 할 때, 이 관계를 확률분포라고 합니다. 그럼 확률변수란 무엇이냐? 무작위로 어떠한 값을 가질 수 있는 변수 정도로 이해하실 수 있을 것 같습니다.
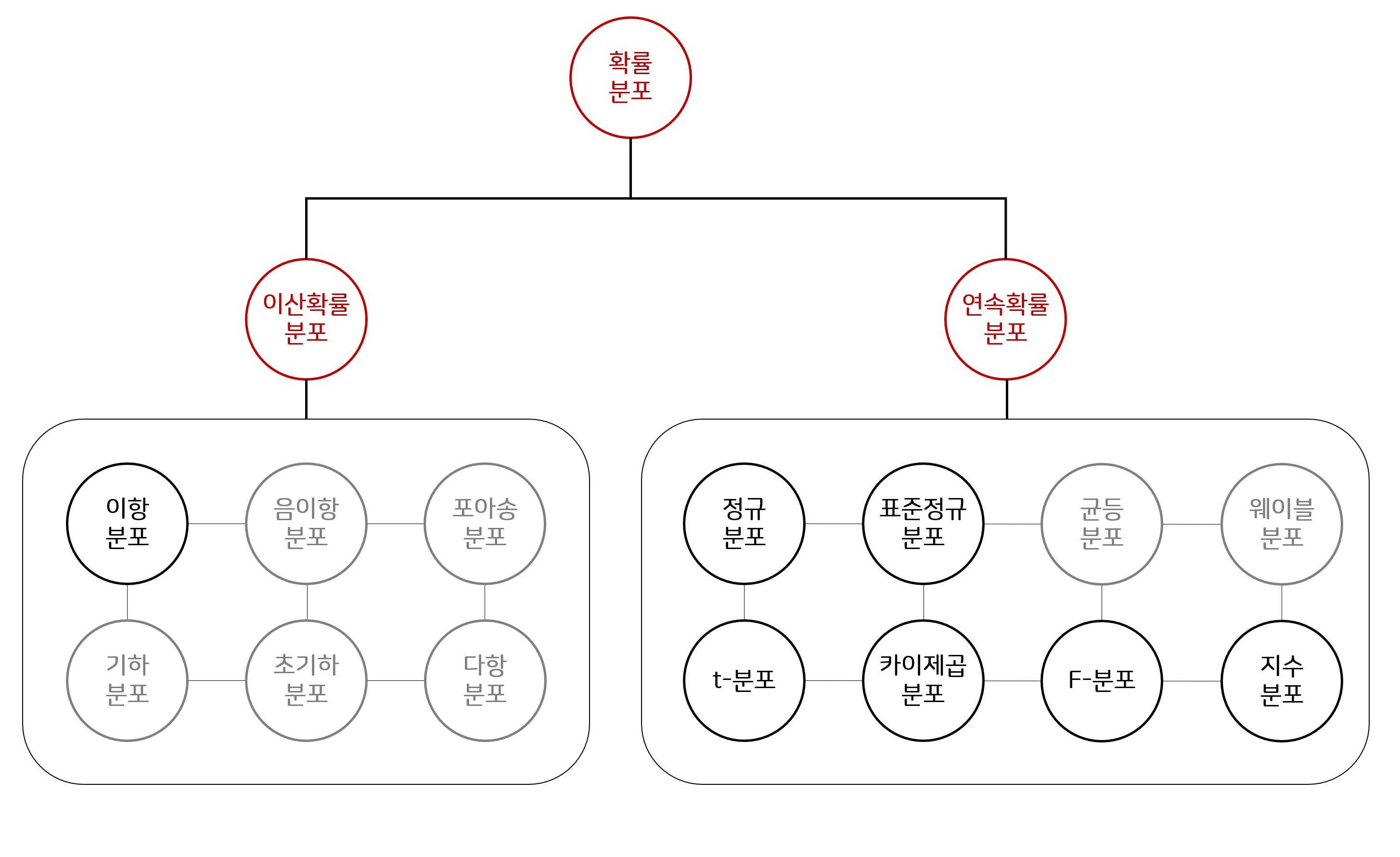
통계분석에 앞서서 일반적으로 알아두어야 할 분포 함수(distribution functions)를 살펴보겠습니다. 첫 번째 그림은 확률분포의 종류를 간략하게 보여주는 것입니다. 일종의 자료생성과정(data generating process)가 어떠한 확률분포를 따라 이루어졌을 것이라고 기대하느냐에 따라 우리는 우리가 얻은 표본의 관측치가 모집단 수준에서는 어떠한 형태의 분포를 가지게 될 것이라고 기대할 수 있고, 그 기대에 따라 다른 통계방법을 사용할 수 있습니다. 위의 분포들 중에는 이 스터디에서 다루지 않는 범위에 있는 분포들이 존재하고, 당장은 굳이 아실 필요가 없다고 생각하여 제외한 분포들도 존재합니다(예, 웨이블 분포, 베타 분포 등). 이전 데이터의 종류에서 살펴보았던 연속형과 이산형의 차이에 유의하셔서 이해하시면 좋을 것 같습니다.
다른 통계분포를 가지고 분석을 할 때, 우리는 종종 그 분포에 기초하여 확률적 진술(probabilistic statements)을 하고는 합니다. 대개 우리가 분포를 통해서 알고 싶은 것은 네 가지로 정리할 수 있습니다.
특정한 값이 확률밀도함수(probability density function)에서 어디에 위치하는지
특정한 값이 누적분포함수(cumulative distribution function)에서 어디에 위치하는지
특정한 확률에 대응하는 분위의 값(quantile value)이 어떻게 되는지
특정한 분포로부터 값을 무작위로 추출(ramdom draw)했을 때의 결과
확률밀도함수는 간단히 얘기하면, “연속확률변수인 \(X\)의 확률을 결정하는 함수”입니다. 즉, 연속형 변수, 0.01, 0.05, 1.23 과 같은 연속적인 값을 가지는 변수가 존재한다고 할 때, 우리가 어떤 값을 뽑을 확률은 그 확률함수에 대한 확률밀도함수로 결정됩니다. 만약 \(X\)가 연속형이 아니라 이산형 변수일 경우에는 \(X\)가 가질 수 있는 값, \(x_1, x_2, x_3, \dots\)에 대한 확률 \(\Pr(X = x_1)\)에 대응하는 관계를 보여주는 함수인 확률질량함수(probability mass function)이 동일한 역할을 수행합니다.
한편, 누적분포함수는 주어진 확률변수에서 어떤 특정한 값과 같거나 작은 값을 뽑을 확률을 보여주는 함수입니다. 그래프로 보면 조금 더 편하실 것 같습니다.
x <- seq(-5, 5, length = 100)
plot(x, dnorm(x), type = "l", col = "#DB3A2F",
ylab = "Density",
xlim = c(-5, 5), ylim = c(0, 1))
text(-3, 0.2, "PDF of Normal Distribution", col = "#DB3A2F")
par(new=TRUE)
plot(x, pnorm(x), type = "l", col = "#275D8E",
ylab = "Density",
xlim = c(-5, 5), ylim = c(0, 1))
text(2, 0.5, "CDF of Normal Distribution", col = "#275D8E")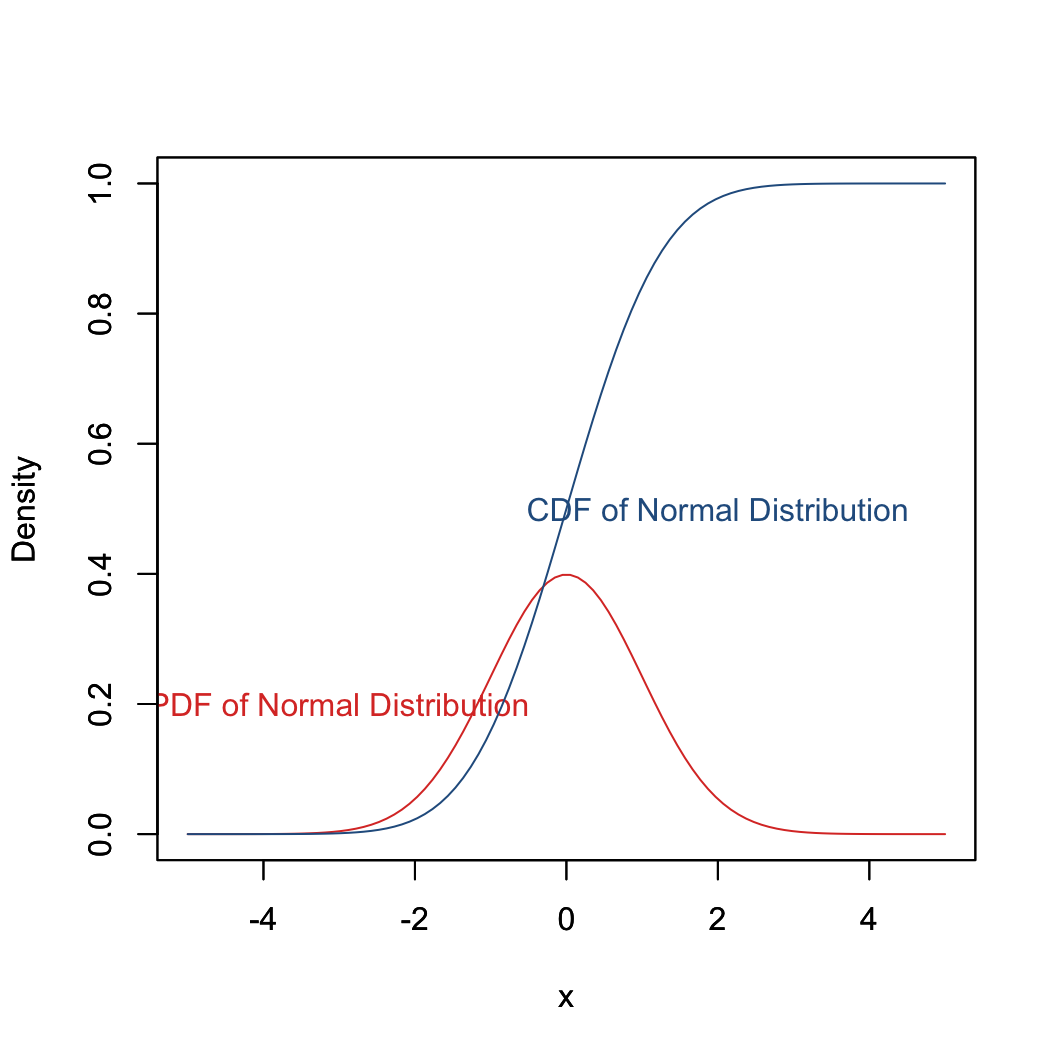
R은 기본적으로 이러한 밀도(density), 분포(distribution), 분위(quantile), 그리고 확률값(random values)을 구할 수 있는 함수를 제공합니다.
dname은 투입된 값x가 확률밀도함수의 어디에 위치하는지를 보여줍니다(density).pname은 투입된 값x가 누적밀도함수의 어디에 위치하는지를 보여줍니다(distribution).qname은 투입된 확률의 분위를 계산해줍니다.,rname은 특정한 분포로부터 무작위로 뽑은 하나의 값을 생성합니다.
예를 들어, 확률변수 \(X\)를 분포, \(N(\mu = 2, \sigma^2 = 25)\)인 분포에서 추출하였다고 하겠습니다. 이때, \(x=3\)일 때의 확률밀도함수의 값을 구해보도록 하겠습니다.
dnorm(x = 3, mean = 2, sd = 5)[1] 0.07820854마찬가지로 \(x=3\)일 때의 누적분포함수의 값을 구하는 것, 즉 \(\Pr(x\leq 3)\)인 값을 구하기 위해서는 다음과 같은 코드를 사용할 수 있습니다.
pnorm(q = 3, mean = 2, sd = 5)[1] 0.5792597확률이 0.975인 경우의 분위수를 구하고 싶다면?
qnorm(p = 0.975, mean = 2, sd = 5)[1] 11.79982마지막으로 표본크기가 10(n=10)인 확률변수를 해당 분포에서 추출하려면?
rnorm(n = 10, mean = 2, sd = 5) [1] 1.3348737 0.9130350 3.9093328 6.2176856 14.1860359 0.5448274
[7] -11.1182227 -3.7093660 4.8861493 8.6717278위의 분포와 관련된 함수는 다른 분포들에도 동일하게 적용되어 뒤의 분포를 나타내주는 단어만 바꿔주면 됩니다.
| Command | Distribution |
|---|---|
| `*binom` | Binomial |
| `*t` | t |
| `*pois` | Poisson |
| `*f` | F |
| `*chisq` | Chi-Squared |
* 뒤의 분포 이름을 d, p, q, r 뒤에 붙임으로써 각 분포에 대한 밀도, 확률, 분위, 무작위 난수에 대한 함수를 적용할 수 있습니다. 예를 들어 dbinom()은 이항분포로부터 값의 밀도를 계산해줍니다. 다만, 정규분포와는 달리 mean과 sd를 가지지 않습니다. 이항분포의 모수는 \(n\)과 \(p\)로 0과 1, 즉 관측치의 개수가 몇개인지를 보여주는 size와 어떤 확률로 0과 1이 분포할 것인지를 의미하는 prob이라는 모수를 설정해주어야 합니다.
dbinom(x= 6, size = 10, prob = 0.75)[1] 0.145998기초적인 분포의 개념을 직관적으로 이해하기 위하여 정규분포(normal distributions)와 이항분포(binomial distributions)로부터 분위(quantiles)를 얻어내는 방법을 살펴보겠습니다.
정규분포 (The normal distribution)
일단 정규분포라는게 어떻게 생겨먹은 놈인지 한 번 살펴보도록 하겠습니다.
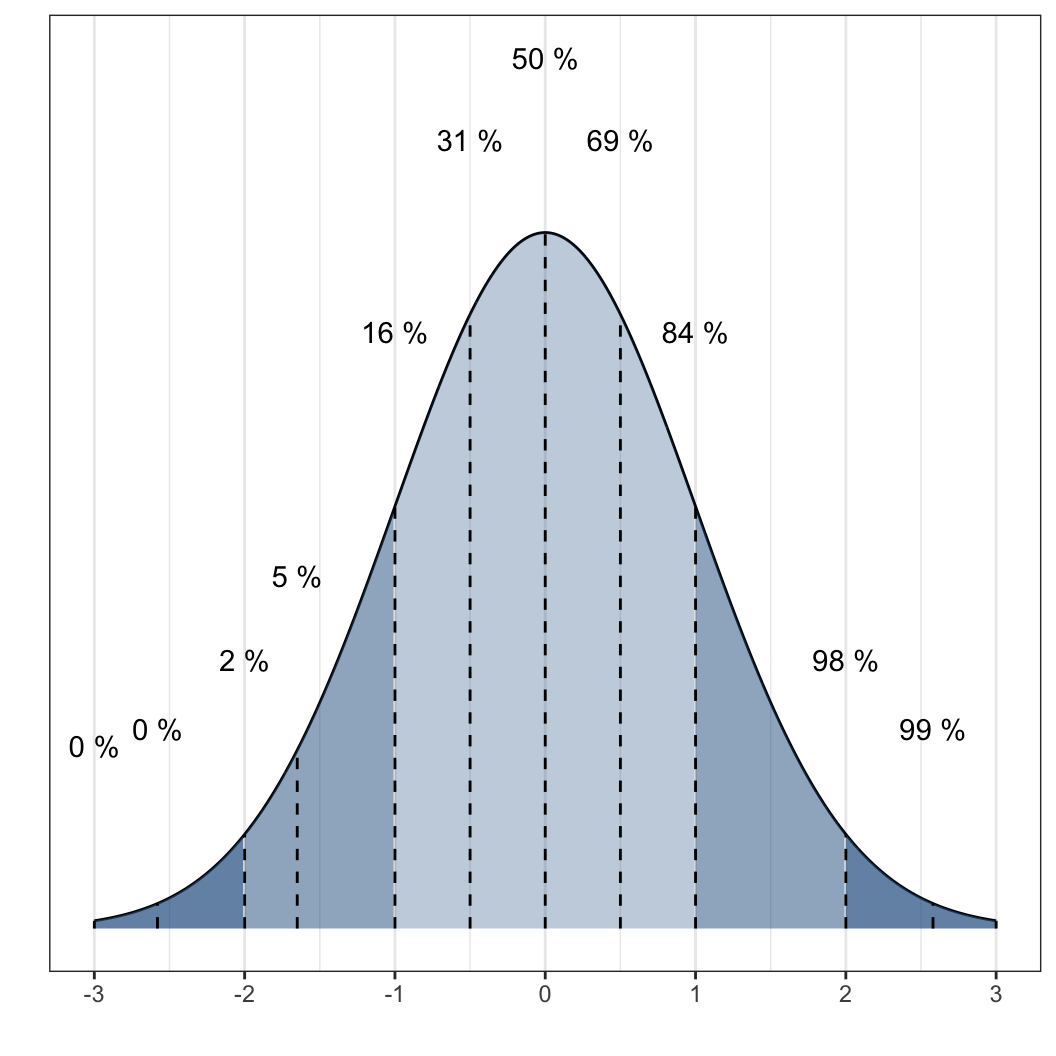
위의 정규분포를 살펴보면, 일종의 기준점(thresholds)을 볼 수 있습니다. 즉, 전체 관측치의 약 2%가 그 기준점보다 값이 작거나 클것 등이 그런 것이죠. 나중에 가설검정과 유의수준에 대한 논의를 할 때 자세하게 살펴보도록 하겠습니다. 수학의 정석 확률과 통계 파트에서 배웠던 1.96 등과 같은 숫자들을 보게 될 것입니다. 위의 정규분포에서 좌측의 끝에 분포한 경우를 좌측꼬리(lower tail), 오른쪽 끝의 분포를 우측꼬리(upper tail)이라고 부릅니다.
pnorm(70, mean = 50, sd = 10, lower.tail = TRUE)[1] 0.9772499pnorm(70, mean = 50, sd = 10, lower.tail = FALSE)[1] 0.022750131 - pnorm(70, mean = 50, sd = 10, lower.tail = TRUE)[1] 0.02275013첫번째 코드는 50을 평균으로 하고 10을 표준편차로 하는 정규분포가 있을 때, 그 분포에서 70이라는 숫자는 어디에 위치하는지를 묻는 것입니다.
두 번째도 동일한 의미인데, 두 식의 차이는 lower.tail 옵션을 어떻게 설정하느냐에 달려있습니다.
각 식이 도출한 결과를 보면 이해하시겠지만 근본적으로 두 식은 동일하며, 좌측에서 누적확률을 계산할 것인지 우측으로부터 계산할 것인지의 차이일 뿐입니다.
간단하게 말하면 첫 번째 식은 70이라는 숫자는 이 분포에서 하위 97.7%에 위치한 값이다라고 말하는 것이고 두 번째 식은 상위 2.2%라고 말하는 것입니다.
따라서 두 번째 식은 전체 확률에서 첫 번째 식으로 계산한 확률을 제한 값과 같으므로 세 번째의 형태로 계산할 수도 있습니다.
그렇다면 만약에 양측꼬리 확률(two-tailed probability)에서 최소한 70만큼 ‘극단적인’(extreme) 확률을 얻고 싶을 때는 어떻게 해야할까요? 이 경우는 생각을 좀 달리 해보면 됩니다. 평균을 기점으로 70은 오른쪽 끝쪽에 위치하는 셈입니다. 그만큼 왼쪽 끝에 위치한 값을 상정하고 그 값이 나올 확률을 함께 계산해주어야 합니다.
이 경우 평균 50에서 70은 20만큼 떨어져 있습니다(우측으로, + 방향). 따라서 우리는 좌측으로 20만큼 떨어진 30이 나올 확률을 함께 고려해주어야 하는 것입니다. 이러한 결과를 얻는 데는두 가지 방법이 존재합니다.
## First
pnorm(70, mean = 50, sd = 10, lower.tail = FALSE) +
pnorm(30, mean = 50, sd = 10, lower.tail = TRUE)[1] 0.04550026## Second
2 * pnorm(70, mean = 50, sd = 10, lower.tail = FALSE)[1] 0.04550026그렇다면 이렇게 구한 분포에서의 누적확률 값을 가지고 분위를 구하여 보겠습니다. 마찬가지로 평균 50에 표준편차가 10인 분포를 상정합니다. 이때 사용할 함수는 qnorm()입니다.
qnorm(0.9772499, mean = 50, sd = 10, lower.tail = TRUE)[1] 70.00001역으로 계산한 것인데, 평균 50에 표준편차 10인 분포에서 좌측부터 앞서 구한 누적확률에 해당하는 값을 구하라는 명령입니다. 앞에서 우리가 입력한 70과 근사한 값을 얻을 수 있습니다. 근소한 차이는 소수점에 의해 발생하는 것으로 이해하시면 됩니다.
다음으로는 주어진 평균 50, 표준편차 10의 분포에서 70이라는 값이 분포에서 차지하는 밀도를 확인해보겠습니다 밀도(density)를 알아보기 위한 함수는 다음과 같습니다.
dnorm(70, mean = 50, sd = 10)[1] 0.005399097그렇다면 이번에는 정규분포에서 관측치를 무작위로 추출(draws)을 해보겠습니다. 이번에도 함수에는 70이라는 값이 사용될 것인데, 여기서 사용되는 70은 특정한 값이 아니라 추출 횟수를 의미합니다.
x <- rnorm(70, mean = 50, sd = 10)
x [1] 43.97510 56.74811 40.56546 52.09211 48.71484 45.49678 33.27438 60.26518
[9] 35.79757 45.16348 44.39599 31.43620 49.10290 47.74355 53.66895 58.22063
[17] 53.39984 51.94731 49.05272 40.86825 49.88982 73.93079 46.49727 50.35070
[25] 39.76499 51.68567 57.48304 44.22915 47.13556 52.91615 62.50642 58.95241
[33] 59.69020 58.14508 58.35131 40.23608 51.78740 51.12004 55.94715 64.32060
[41] 44.38094 56.31792 48.07166 23.27829 40.85056 44.80070 52.62612 48.42972
[49] 41.26224 50.69592 32.04993 33.83697 64.89256 53.46143 44.30335 49.94032
[57] 54.96654 83.95703 62.98055 47.14896 45.84600 49.11855 64.47021 63.76422
[65] 37.21350 44.02801 57.29268 27.46894 49.26964 49.80080총 70개의 값이 무작위로 추출되어 x라는 벡터에 담겨 있는 것을 확인할 수 있습니다.
이번에는 좀 더 구체적으로 정규분포 사례들을 살펴보겠습니다. 서로 다른 평균(mean)과 표준편차(standard deviation)를 가지는 세 개의 정규분포를 그려보겠습니다.
normal5 <- rnorm(n = 10000, mean = 5, sd = 3)
normal50 <- rnorm(n = 10000, mean = 50, sd = 10)
normal20 <- rnorm(n = 10000, mean = 20, sd = 1)세 함수 모두 표본의 크기는 1만 개이며, 각자 다른 평균과 표준편차를 따르는 정규분포를 가정하여 무작위로 추출된 값을 담는 벡터로 출력됩니다. 이렇게 값을 갖는 세 개의 벡터를 하나의 데이터로 합쳐보겠습니다. 간단하게 말하면 하나의 표로 합친다는 것과 같습니다.
norm <- bind_rows(tibble(x = normal5, Mean = 5, SD = 3),
tibble(x = normal50, Mean = 50, SD = 10),
tibble(x = normal20, Mean = 20, SD = 1))
norm <- norm %>% mutate(
Mean = as.factor(Mean))그리고 이렇게 만들어진 데이터프레임의 평균 값을 Factor 자료 유형으로 변환해줍니다. 이것이 의미하는 게 뭘까요? 평균5, 평균50, 평균20을 문자열로 인식하게 하여 일종의 “이름”으로 인식하게 만드는 것입니다. 그러면 이제 이렇게 만들어진 데이터로 그래프를 그려보겠습니다.
ggplot(norm, aes(x = x, fill = factor(Mean))) +
geom_density(adjust = 4, alpha = 1/2) +
guides(color=guide_legend(title = "Mean, SD")) +
guides(fill=guide_legend(title = "Mean, SD")) +
scale_fill_manual(values = futurevisions("mars")) +
scale_color_manual(values = futurevisions("mars")) +
labs(x = "") +
theme(legend.position = "top")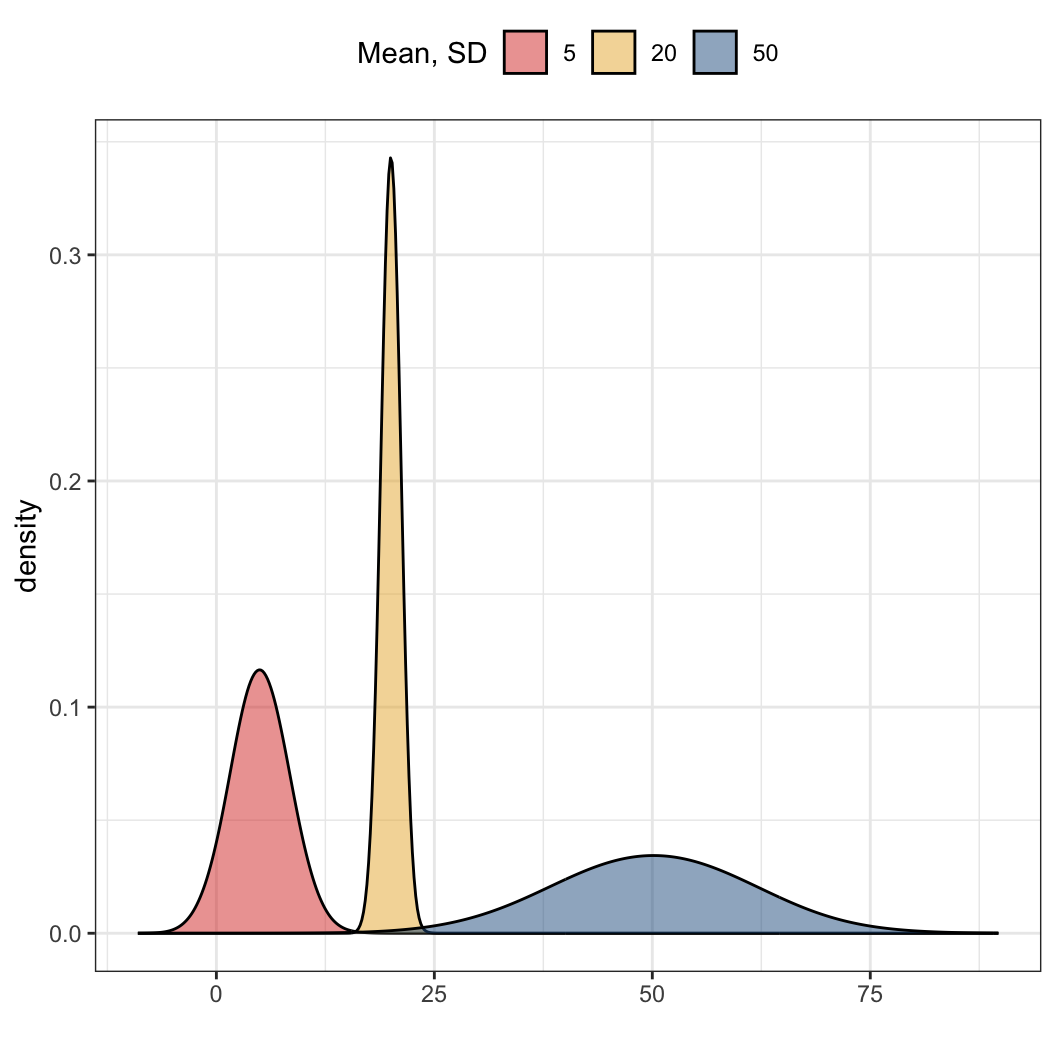
ggplot2 패키지는 R에서 그래프를 그리는 데 있어서 유용하게 사용됩니다. 먼저 ggplot2 패키지를 불러오고 나서, ggplot(데이터프레임 이름, aes(x = x축으로 삼을 변수이름))을 설정하면 일단 수학적으로 지정한 데이터의 변수에 대한 기본적인 작업은 진행이 됩니다.
그러나 이 단계에서는 아직 가시화(visualization)라고 할 수는 없는데, 주어진 데이터를 컴퓨팅했을 뿐이지 어떻게 가시적인 형태로 보여주라는 명령을 부여하지 않았기 때문입니다. 컴퓨터로 그림을 그려본 사람들은 이해가 쉬운데, ggplot()은 레이어 시스템을 이용해서, 우리가 뭔가 그려진 걸 얻고 싶을 때마다 레이어를 하나씩 추가해서 보여달라고 R에게 요구해야만 합니다.
그리고 이때, 레이어를 추가하는 것은 +로 가능합니다. 하나씩 뜯어서 보면,
ggplot(norm, aes(x = x)) +:ggplot2패키지를 이용하여norm이라는 데이터 프레임에서x축에는x라는 변수를 기준으로 늘어놓아라. 그리고 뒤에 더해지는 레이어 명령을 덮어 씌워라 라는 의미의 코드입니다.geom_density(aes(fill = as.factor(Mean)), adjust = 4, alpha = 1/2) +: 밀도함수의 형태로 그래프를 그리되,Mean이라는Factor변수가 같은 것들 끼리 같은 색으로 칠해서 보여주어라 라는 코드입니다.- 뒤의 옵션은 세세한 조정이니 굳이 언급하지는 겠습니다.
- 뒤에 더해지는 옵션들은 레이어를 추가하여 기존의 코드에 덮어 씌워, 그래프를 덧칠하는 역할을 합니다.
guides(color=guide_legend(title = "Mean, SD")): 우측에 더해지는 그래프 테두리의 범례의 이름을 어떻게 지으라는 명령입니다.guides(fill=guide_legend(title = "Mean, SD")): 우측에 더해지는 색을 채우는 범례의 이름을 어떻게 지으라는 명령입니다.- 이 경우에는 색도 있고 그래프를 선명하게 보여주는 선도 있기 때문에 그 각각이 레이어를 이루고 있어 둘 모두에게 이러한 명령어를 적용해야 합니다.
scale_color_discrete(labels = c("5, 3", "20, 1", "50, 10")):color를 뒤에 이어지는 라벨로 구분해주라는 코드입니다.
++ scale_fill_discrete(labels = c("5, 3", "20, 1", "50, 10")) +: fill을 뒤에 이어지는 라벨로 구분해주라는 코드입니다.
- ggtitle(
Probability Density Function\nNormal Distribution) : 표 전체의 이름을 지정하는 명령어이고,\n은 R에서는 강제 개행(enter)하는 명령어입니다.
\(t\) 분포 (Student’s \(t\); the \(t\) distribution)
\(t\) 분포는 거의 정규분포와 비슷합니다.
\(t\) 분포를 이용한 방법은 더블린의 기네스 맥주공장에서 일하던 통계학자 William Gosset에 의해서 1908년에 고안되었습니다. 회사 정책 상 자신의 이름으로 논문을 내는 것이 불가능했기 때문에, Gosset은 가명으로 Student라는 이름을 이용하여 논문을 작성하였습니다. 때로 Student’s \(t\)라고 불리는 이유는 그 때문입니다. 공장에서 Gosset에게는 테스트할 맥주 표본이 매우 소수만 제공되었기 때문에, 그는 그 표본사례를 가지고 기존의 표준오차 공식의 정규 \(z\)-score에 사용할 수 없다는 것을 알게 되었습니다. 그 결과가 소수의 사례로 구성된 꼬리가 정규표준분포에 비해 약간 더 두꺼운 \(t\) 분포입니다. 자세한 내용은 다음에 다루도록 하겠습니다.
특징으로는
0을 중심으로 종 형태(bell-shaped)를 취하는 분포
표준편차는 1보다 조금 큰 분포; 따라서 표준정규분포보다 양 꼬리가 조금은 더 두꺼운 모습을 보임.
정확한 형태는 자유도(degree of freedom)를 따르는데, 평균을 추론할 때 자유도는 대개 전체 표본규모에서 -1을 취한 값을 의미함.
자유도가 증가함에 따라 \(t\) 분포는 표준정규분포와 거의 흡사해짐.
따라서 표본규모가 커질수록 우리는 \(t\) 분포가 정규분포에 수렴할 것이라고 기대할 수 있음.
평균에 대한 신뢰구간은 오차한계를 \(t(se)\)로 갖게 됨.
이항분포 (Binomial distribution)
이항분포는 우리에게 n번의 시행에서 k번 성공할 확률을 보여주는 분포입니다. 단순하게 말하자면 0과 1의 값만 갖는다고 가정된 벡터가 있다고 하겠습니다. 이때 벡터의 요소의 총 개수는 100개이고 랜덤으로 0과 1 중 하나가 벡터에 들어간다고 할 수 있습니다. 이때 전체 요소의 수 100개 중 1이 뽑혔을 경우를 계산하면 결국 1을 뽑을 성공 사례의 총합을 100으로 나눔으로써, 전체 대비 성공의 확률을 구하는 것이라 할 수 있습니다. 즉, 정규분포에서와는 다르게 이항분포에서는 평균(mean)이 아니라 비율(proportion)에 초점을 맞추게 됩니다.
pbinom(27, size=100, prob=0.25, lower.tail = TRUE)[1] 0.7223805시도가 성공할 확률을 0.25라고 놓고 시행 횟수를 100번으로 가정한 경우입니다. 즉, 100번 시도했을 때 성공할 확률이 25%인 이항분포를 가지는 데, 실제로는 27번 성공했다고 한다면 누적확률에서 어느 위치에 해당하는지를 묻는 함수입니다. lower.tail()이 TRUE로 설정되어 있으므로 좌측에서부터 계산한 것입니다. 즉, 27번 성공한 것은 하위 72.2%, 상위 27.8%에 해당한다는 것을 알 수 있습니다.
qbinom(0.7223805, size = 100, prob = 0.25, lower.tail = TRUE)[1] 27이렇게 구한 누적확률로 다시금 성공 횟수를 추정해보겠습니다. 정규분포때와 거의 유사합니다. size = 100은 서로 독립적인 사건의 시행, 즉 베르누이 시행(Bernoulli trials)의 횟수를 의미합니다. 그렇다면 100번 시도했을 때 27번 성공할 정확한 확률을 구해보겠습니다.
dbinom(27, size=100, prob=0.25)[1] 0.08064075choose(100, 27)*.25^27*(1-.25)^(100-27)[1] 0.08064075두 가지 방법으로 구할 수 있는데, 첫 번째는 R에 내장된 기본 함수인 dbinom()으로 구하는 것입니다. 두 번째는 choose() 함수를 이용해서 구하는 것입니다. 개인적으로는 dbinom() 함수가 있는데 굳이 choose() 함수 사용법까지 알아야 하나 싶기는 합니다. 그러나 choose() 함수로 보여지는 식이 좀 더 직관적으로 이해하기에는 도움이 됩니다.
rbinom(27, size=100, prob=0.25) [1] 21 23 29 22 24 25 20 21 30 22 29 25 28 25 25 17 30 33 27 31 20 22 15 29 31
[26] 25 21sd(rbinom(27, size=100, prob=0.25))[1] 4.906243마지막으로는 0.25의 확률을 가진 100번의 베르누이 시행을 27번을 반복하는 결과를 보여줍니다. 즉, 평균적으로는 100번 시행 중 25번의 성공을 할 것으로 기대되지만, 실제 시행을 27번 해보면 무작위 추출이기 때문에 25를 중심으로 표준편차 4.21의 범위 내에서 여러 값들이 추출되는 것을 확인할 수 있습니다. 무작위로 추출하기 때문에 돌릴 때마다 값은 다르게 나올 것입니다.
다시 한 번, n번의 독립적인 베르누이 사건을 시행할 때, k번 성공할 확률을 구하는 이항분포로 실습해보겠습니다. 구체적으로 모집단의 성공 확률을 p, 모집단의 크기를 n으로 특정하겠습니다.
binom10 <- rbinom(n = 10000, p = .5, size = 10)
binom50 <- rbinom(n = 10000, p = .5, size = 50)
binom100 <- rbinom(n = 10000, p = .5, size = 100)정규분포와 다르지는 않습니다. 다만 여기서의 size는 전체 동전을 던지는 횟수로 이해하면 되고 10,000은 그렇게 동전을 10번, 50번, 100번 던지는 걸 10,000번 반복한다는 의미라고 할 수 있습니다. 그럼 이제 마찬가지로 하나의 데이터프레임으로 세 번의 시도(binom10, binom50, binom100)의 결과를 합쳐주고 그래프를 그려보겠습니다.
binom <- bind_rows(tibble(k = binom10, Size = 10),
tibble(k = binom50, Size = 50),
tibble(k = binom100, Size = 100)) %>%
mutate(Size = as.factor(Size))
ggplot(binom, aes(x = k)) +
geom_density(aes(group = Size, color = Size, fill = Size),
adjust = 4, alpha = 1/2) +
scale_color_manual(values = futurevisions("mars")) +
scale_fill_manual(values = futurevisions("mars")) +
labs(x = "") +
theme(legend.position = "top")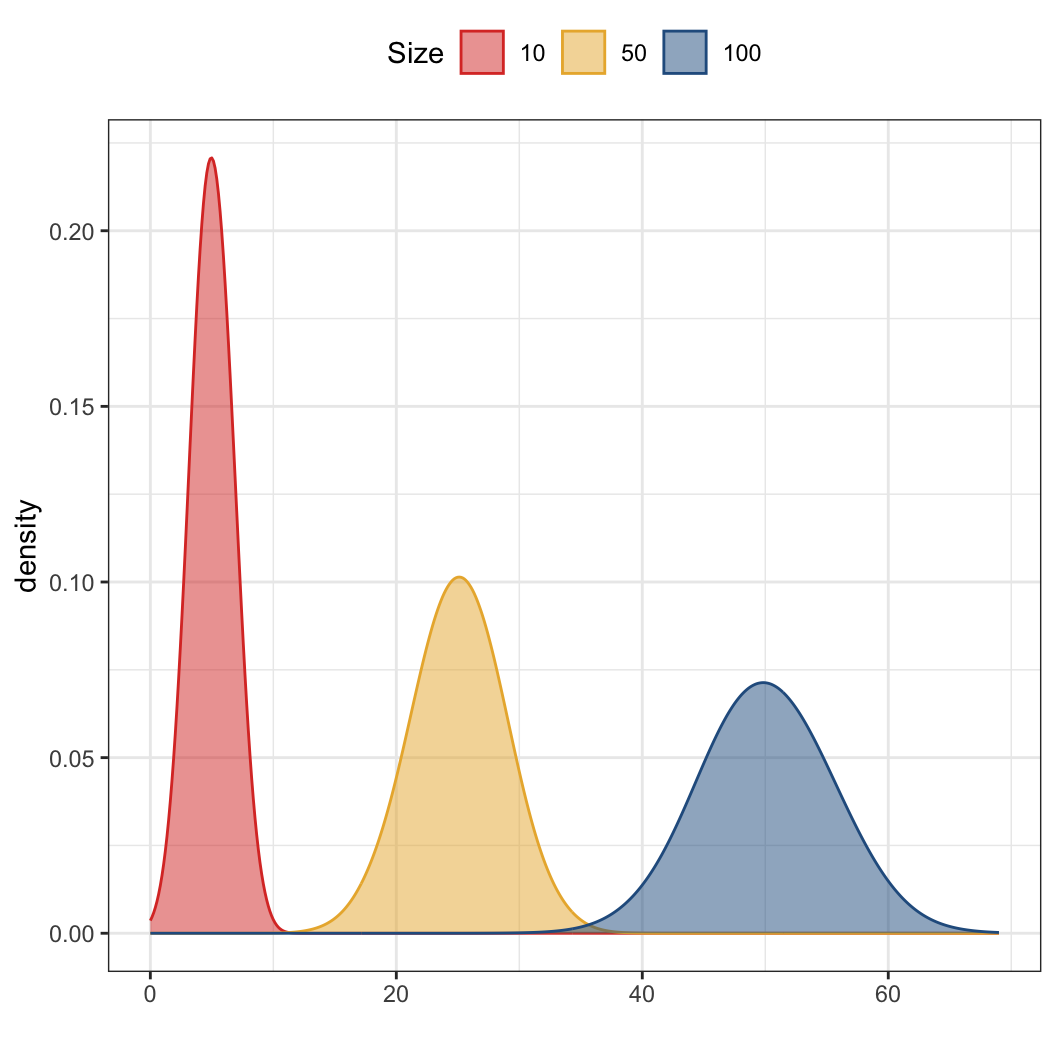
포와송 분포 (Poisson distribution)
이 포스팅은 주로 R 코드에 관한 것이기 때문에 분포에 대한 수리통계적인 설명은 가급적 피하도록 하겠습니다. 포와송 분포는 고정된 대규모 모집단(fixed large population)에서 짧은 시간에 걸쳐서 희소한 사건(rare events)의 발생 횟수를 추정하는 데 용이한 분포입니다.
포와송 분포에서 그 희소한 사건의 발생 확률은 시간 단위 별 발생의 평균 횟수로 나타나며 그리스어 람다(Lambda, \(\lambda\))로 표기됩니다. 람다는 평균과 분산을 결정합니다.
포와송 분포의 확률을 이용해서 우리는 단일 시간 단위에서 k라는 희소한 사건을 정확하게 관측할 확률을 기술할 수 있습니다. 나머지는 앞의 정규분포랑 이항분포에서 했던 코드를 기계적으로 반복해서 살펴보는 것과 같습니자. 단, 포와송 분포에서 코드 중에는 이전과 다른 부분이 있으니 그 점만 유의하면 될 것 같습니다.
pois1 <- rpois(n = 10000, lambda = 1)
pois2 <- rpois(n = 10000, lambda = 2)
pois5 <- rpois(n = 10000, lambda = 5)
pois20 <- rpois(n = 10000, lambda = 20)
pois <- tibble(Lambda.1 = pois1,
Lambda.2 = pois2,
Lambda.5 = pois5,
Lambda.20 = pois20)
pois# A tibble: 10,000 × 4
Lambda.1 Lambda.2 Lambda.5 Lambda.20
<int> <int> <int> <int>
1 1 3 4 19
2 1 3 2 19
3 2 3 6 20
4 3 1 6 24
5 3 2 2 15
6 0 3 6 17
7 0 0 1 24
8 0 1 4 16
9 1 0 2 26
10 0 0 3 16
# ℹ 9,990 more rows이번에는 만들어진 pois라는 데이터를 tidyr의 gather() 함수를 이용해서 다른 변수로 재구성해줄 것입니다. 또한 정해진 값에서 변수명으로 변환할 때 문자열을 추출하기 위한 str_extract() 함수는 stringr 패키지에서 로드하도록 하겠습니다.
pois <- pois %>% tidyr::gather("Lambda", "x")
pois # gather 함수를 이용해 wide -> long으로 바뀐 데이터# A tibble: 40,000 × 2
Lambda x
<chr> <int>
1 Lambda.1 1
2 Lambda.1 1
3 Lambda.1 2
4 Lambda.1 3
5 Lambda.1 3
6 Lambda.1 0
7 Lambda.1 0
8 Lambda.1 0
9 Lambda.1 1
10 Lambda.1 0
# ℹ 39,990 more rowspois <- pois %>% mutate(
Lambda = Lambda %>%
str_remove("Lambda.") %>%
parse_factor(.,
levels = c("1", "2", "5", "20"),
ordered = T, include_na = F)
)
pois # Lambda라는 문자열을 지우고 숫자만 factor 로 변환# A tibble: 40,000 × 2
Lambda x
<ord> <int>
1 1 1
2 1 1
3 1 2
4 1 3
5 1 3
6 1 0
7 1 0
8 1 0
9 1 1
10 1 0
# ℹ 39,990 more rows처음 만든 pois 데이터에서 tidyr의 gather()를 이용해서 Lambda라는 변수 아래에 1, 2, 5, 20의 라벨을 길게(long-shape) 합쳤습니다. 그리고 마지막으로는 Lambda 변수의 문자열 Lambda.을 제외한 라벨 숫자만 남겨놓은 것입니다. 결과적으로 Lambda 변수에는 각 Lambda 값이 얼마였는지를 나타내는 순위를 가진 요인형 변수값만 남았습니다. 이렇게 만들어진 포와송 분포의 값들을 하나의 그래프로 만들어서 시각화해보도록 하겠습니다.
ggplot(pois, aes(x = x)) +
geom_density(aes(group = Lambda,
color = Lambda,
fill = Lambda),
adjust = 4, alpha = 1/2) +
scale_color_manual(values = futurevisions("mars")) +
scale_fill_manual(values = futurevisions("mars")) +
labs(x = "") +
theme(legend.position = "top")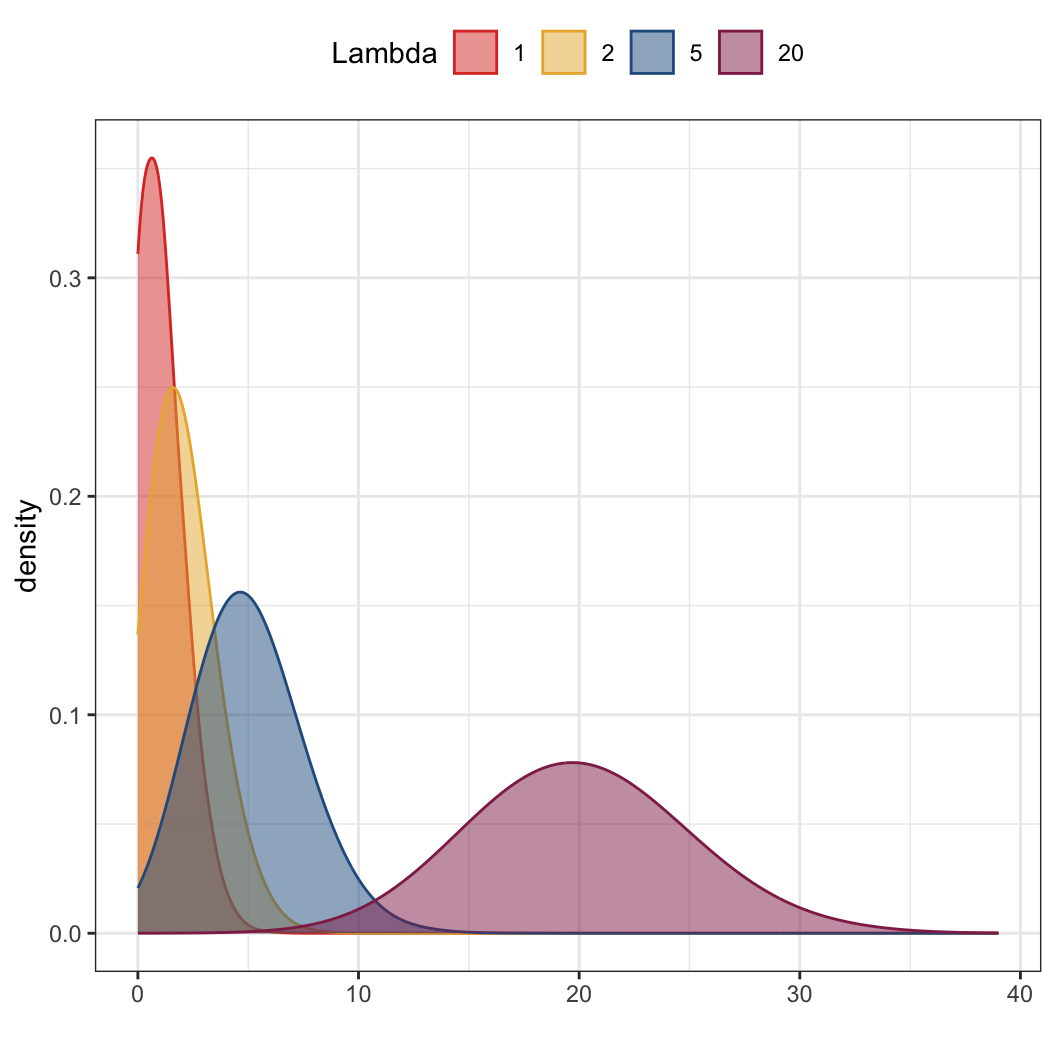
음이항 분포 (Negative Binomial Distribution)
음이항 분포는 n번째 시도에서 k번째에 성공할 확률을 보여줍니다. 음이항 분포는 다음과 같은 네 조건이 충족될 때 유용합니다.
- 모든 시도는 독립적이다.
- 각 시도의 결과는 성공 혹은 실패로 구분될 수 있다.
- 성공 확률 (
p)은 각 시도마다 동일하다. - 마지막 시도는 항상 성공이어야만 한다.
여기서 보면 알 수 있듯이, 처음 세 조건은 이항분포와 동일합니다. 세 개의 음이항 분포 결과를 계산하여 세 개의 벡터로 저장하겠습니다. 그리고 이걸 마찬가지로 하나의 데이터로 합칩니다.
nbinom1 <- rnbinom(n = 10000, p = .3, size = 1)
nbinom5 <- rnbinom(n = 10000, p = .3, size = 5)
nbinom10 <- rnbinom(n = 10000, p = .3, size = 10)
nbinom <- bind_rows(tibble(x = nbinom1, Size = 1),
tibble(x = nbinom5, Size = 5),
tibble(x = nbinom10, Size = 10)) %>%
mutate(Size = as.factor(Size))포와송이랑 이항분포에서 사용했던 함수들과 거의 유사합니다. 이렇게 만들어진 그래프는 다음과 같습니다.
ggplot(nbinom, aes(x = x)) +
geom_density(aes(group = Size, color = Size, fill = Size),
adjust = 4, alpha = 1/2) +
scale_color_manual(values = futurevisions("mars")) +
scale_fill_manual(values = futurevisions("mars")) +
labs(x = "") + theme(legend.position = "top")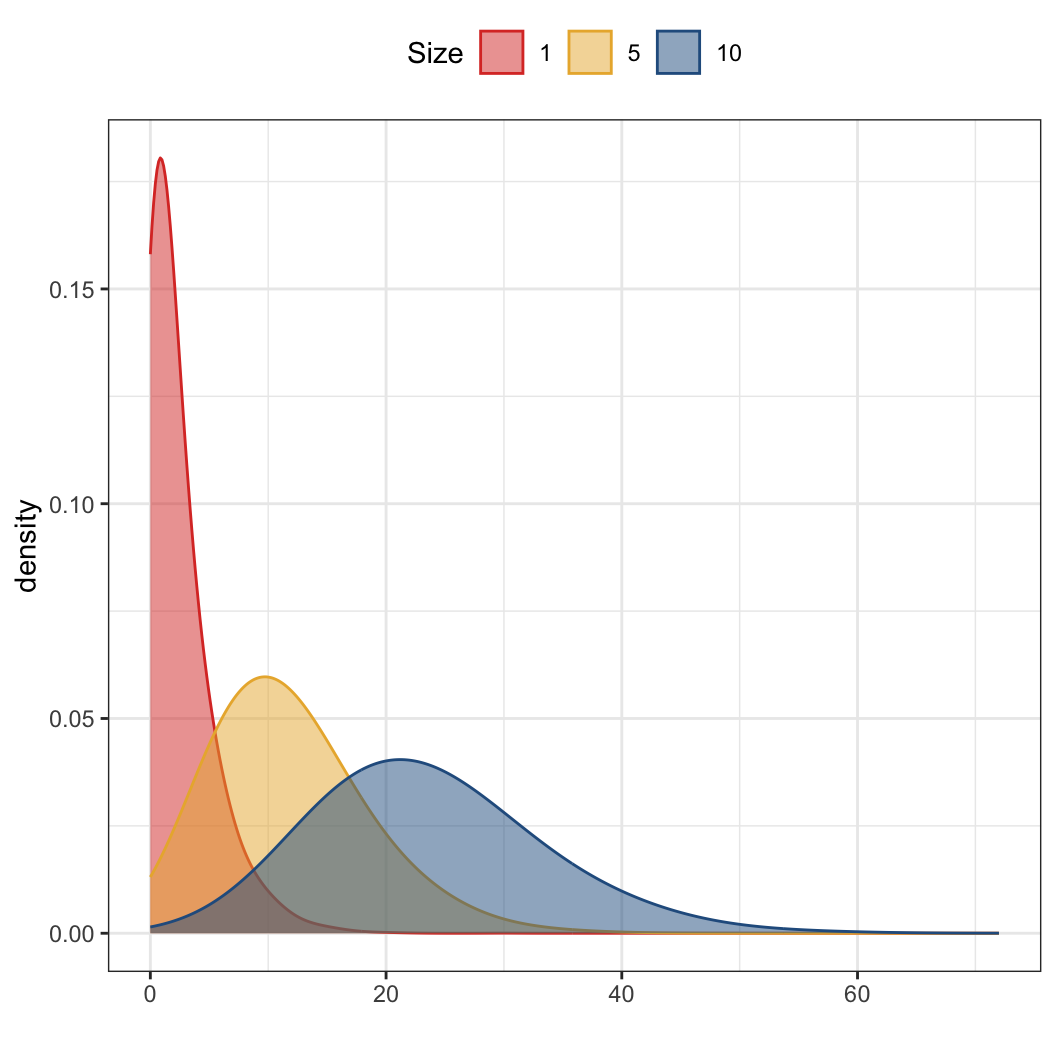
F 분포 (F Distribution)
rf()를 통해서 F 분포에서 무작위로 10,000개의 값을 서로 다른 자유도를 이용하여 추출하여 네 개의 벡터에 저장합니다. 이제는 아시겠지만 rf()의 r은 random을 의미합니다.
fa <- rf(n = 10000, df1 = 1, df2 = 50)
fb <- rf(n = 10000, df1 = 5, df2 = 100)
fc <- rf(n = 10000, df1 = 50, df2 = 50)
fd <- rf(n = 10000, df1 = 50, df2 = 500)
f <- bind_rows(tibble(x = fa, DF1 = 5, DF2 = 5),
tibble(x = fb, DF1 = 5, DF2 = 10),
tibble(x = fc, DF1 = 10, DF2 = 5),
tibble(x = fd, DF1 = 10, DF2 = 10))이렇게 만들어진 데이터의 결과는 그림과 같습니다. 그리고 이제 x 값이 6보다 작거나 같은 경우로 하위 데이터를 만듭니다. 왜냐하면 굉장히 극단적인 수치들이 희소한 확률로 있기 때문에 그냥 그래프를 그리면 집단 별 차이를 보기가 조금 힘들 수도 있기 때문입니다. 그리고 전체 자유도를 지정해줄 것입니다. 자세한 내용은 나중에 F-distribution을 언급할 때 설명하도록 하겠습니다.
f <- f %>% dplyr::filter(x <= 6) %>%
mutate(DF = DF1 * 100 + DF2) %>%
mutate(DF = as.factor(DF))
ggplot(f, aes(x = x)) +
geom_density(aes(color = DF, fill = DF),
adjust = 4, alpha = 1/2) +
guides(color=guide_legend(title = "DF1, DF2")) +
guides(fill=guide_legend(title = "DF1, DF2")) +
scale_color_manual(
values = futurevisions("mars"),
labels = c("1, 50", "5, 500", "50, 50", "50, 500")) +
scale_fill_manual(
values = futurevisions("mars"),
labels = c("1, 50", "5, 500", "50, 50", "50, 500"))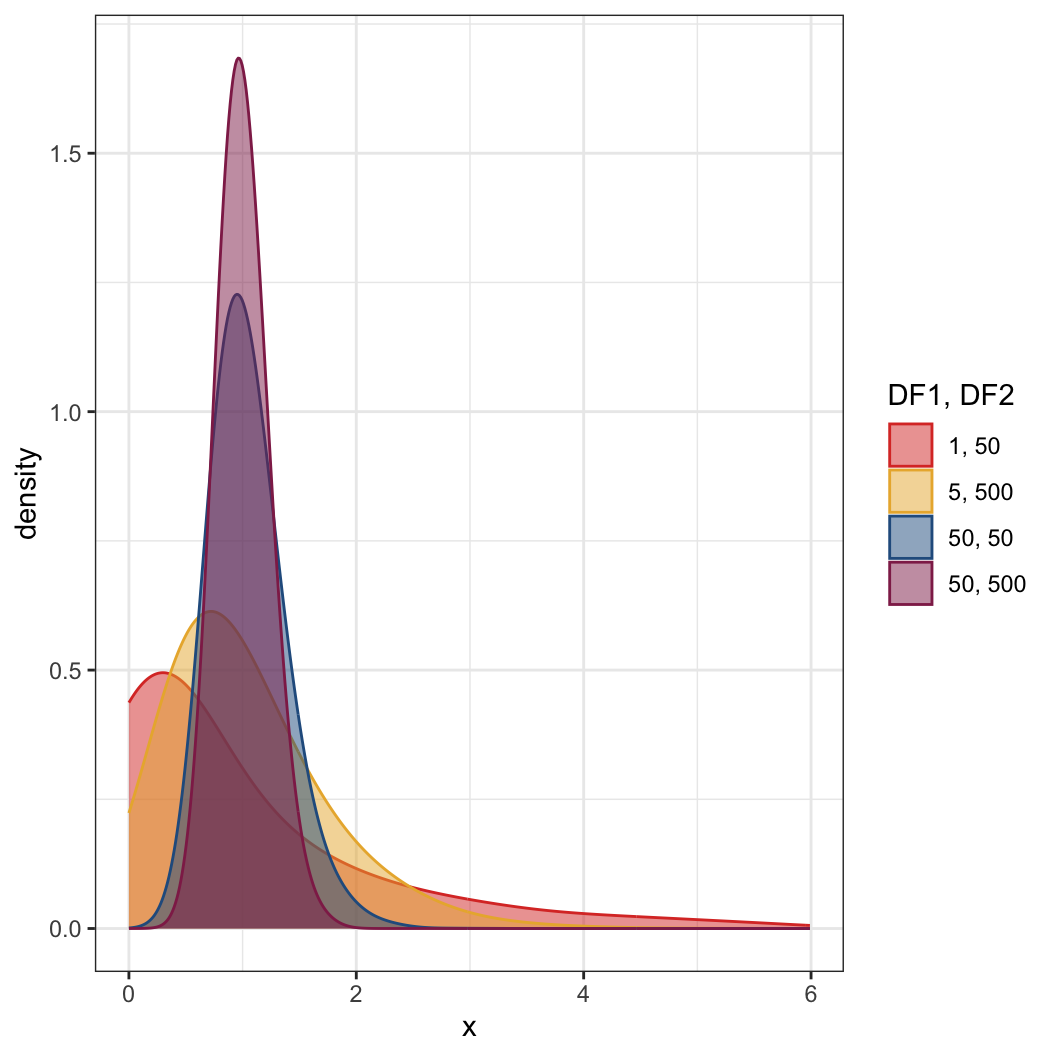
DF1이랑 DF2를 합쳐준다는 것은 F-분포의 특징 때문인데, 간단하게 말하자면 t-분포와 다르게 F-분포는 분자, 분모에 자유도가 하나씩 즉 2개가 필요하기 때문입니다.
오늘 포스팅한 내용 중에서는 처음 두 분포, 정규분포와 이항분포에 대해서는 숙지할 필요가 있고 나머지 분포들은 추후에 다시 다룰 기회가 있을 것이라고 생각합니다. 사실 분포는 엄청 많습니다: 웨이블, 토빗… 뭐 여럿 있기 때문에 다 외우는 것은 어렵고 여기서는 단지 R-code로 구현하는 방법을 러프하게 살펴보았다고 할 수 있을 것입니다.
그리고 ggplot()은 손에 익도록 연습하는 것이 좋습니다. R의 장점 중 하나는 여타의 통계툴들에 비해 그래프 기능이 뛰어나다는 것입니다. ggplot()은 R이 그러한 명성을 얻게 해 준 공신 중 하나라고 할 수 있습니다.
Hypothesis Tests in R
이 워크샵에서의 핵심 중 하나는 가설검정에 대한 기초를 이해하는 것입니다. 가설검정의 구조는 다음과 같이 정리할 수 있습니다.
전체적인 모델과 그 모델에 관계된 일련의 가정들을 수립한다.
- 예를 들면, 관측치들이 정규분포를 따른다는 가정 등.
영가설(null hypothesis; \(H_0\))과 대안가설(혹은 연구가설; alternative hypothesis, research hypothesis; \(H_1\), \(H_A\))을 수립한다. 대개 영가설은 모수가 어떤 값을 것이라고 특정한 값을 고정적으로 설정한다.
주어진 데이터를 가지고 검정통계치(test statistics)의 값을 계산한다.
일반적인 가정 하에서, 영가설이 참이라는 가정 하에 검정통계량의 분포(distribution)는 알려져 있다.
주어진 분포와 검정통계치 값을 가지고 우리는 \(p\)-값을 계산할 수 있다.
\(p\)-값과 사전에 특정한 신뢰수준의 값에 따라서 다음과 같은 결정을 내릴 수 있다.
영가설을 기각하는 데 실패하거나
영가설을 기각하거나
단일표본(One Sample) t-Test
\(x_i\sim \mathrm{N}(\mu,\sigma^2)\)라고 할 때, 우리는 \(H_0 : \mu=\mu_0\)이라는 영가설을 \(H_1 : \mu \neq \mu_0\)이라는 대안가설에 미루어 검정하게 됩니다. 이때, \(\sigma\)가 알려져 있다고 가정하면 우리는 단일표본 스튜던트 \(t\) 검정 통계량을 사용할 수 있습니다.
\[ t = \frac{x-\mu_0}{s/\sqrt{n}}\sim t_{n-1},\\ \text{where}\: x = \frac{\sum^n_{i=1}x_i}{n}\:\text{and}\:s=\sqrt{\frac{n-1}{1}\sum^{n}_{i=1}(x_i-x)^2}, \]
\(\mu\)에 대한 \(100(1-\alpha)\)%에서의 신뢰구간은 다음과 같이 계산할 수 있습니다.
\[ x \pm t_{n-1}(\alpha/2)\frac{s}{\sqrt{n}} \]
그리고 이때 \(t_{n-1}(\alpha/2)\)는 \(n-1\)의 자유도에서 \(\Pr(t>t_{n-1}(\alpha/2))=\alpha/2\)로 계산되는 결정값(critical value)입니다.
단일표본 t-Test: Example
어떤 가게에서 16온스짜리 시리얼 박스를 판다고 가정해보겠습니다. 9개의 박스를 무작위로 꺼내서 무게를 재보았더니 다음과 같습니다.
capt_crisp =
data.frame(weight = c(15.5, 16.2, 16.1, 15.8, 15.6,
16.0, 15.8, 15.9, 16.2))시리얼을 만드는 회사는 박스 당 평균 무게는 적어도 16온스가 된다고 주장하고 있습니다. 우리가 시리얼 박스의 무게가 정규분포를 따르고, 회사의 주장에 대해 신뢰수준 0.05 수준에서 이를 검정해본다고 하면 영가설은 \(H_0: \mu \geq 16\), 즉 16온스보다 크거나 같을 것이다, 대안가설은 \(H_A: \mu < 16\), 16온스보다 작다라고 할 수 있습니다. 그리고 검정통계량은 다음과 같습니다.
\[ t = \frac{x-\mu_0}{s/\sqrt{n}} \]
이때, 표본의 평균 \(x\)와 표본의 표준편차 \(s\)는 R로 간단히 계산할 수 있습니다. 그리고 가설에 필요한 평균과 표본규모도 쉽게 확인할 수 있습니다.
x_bar <- mean(capt_crisp$weight)
s <- sd(capt_crisp$weight)
mu_0 <- 16
n <- 9검정통계량은 다음과 같이 구할 수 있습니다.
t <- (x_bar - mu_0) / (s / sqrt(n))
t[1] -1.2주어진 영가설 하에서 검정통계량은 \(n-1\) 자유도에서 \(t\) 분포를 따릅니다. 즉, 9개의 박스를 뽑았으니 자유도는 8이 됩니다. 검정에 대한 \(p\)-값을 구하기 위해서 단측 검정을 실시합니다. 단측이라고 하는 이유는 이미 영가설을 통해 우리가 관계의 방향을 상정했기 때문입니다. 즉, 특정한 값에 비해 크다, 작다라는 한쪽 방향만을 검정하면 되기 때문입니다.
\[ \Pr(t_s < -1.2) \]
pt(t, df = n - 1)[1] 0.1322336이제 검정에 대한 \(p\)-값을 확보하였으니, 이것이 신뢰수준에 비해 더 큰지, 즉 영가설을 기각할 충분한 근거를 가지는지를 확인해보면 됩니다.
t.test(x = capt_crisp$weight,
mu = 16, alternative = c("less"),
conf.level = 0.95)
One Sample t-test
data: capt_crisp$weight
t = -1.2, df = 8, p-value = 0.1322
alternative hypothesis: true mean is less than 16
95 percent confidence interval:
-Inf 16.05496
sample estimates:
mean of x
15.9 자, 하나씩 뜯어보겠습니다.
\(t\) 값은 -1.2이고, 자유도는 8, \(p\)-값은 0.1322입니다.
대안가설은 모평균(시리얼 박스의 모집단이 가지는 무게의 평균)이 16온스보다 작을 것이다, 입니다.
- 만약 우리가 영가설을 기각하지 못한다면 우리는 대안가설을 믿을만한 경험적 근거를 확보했다고 볼 수 있을 것입니다.
단측검정을 했기 때문에,
R은 한쪽 신뢰구간만 제시합니다. 일단 위의 결과에 따르면 \(p\)-값은 0.1322, 즉 신뢰수준 0.05보다 큽니다.이 결과는 100개의 표본을 뽑아서 평균을 내보았을 때, 약 13개에 해당하는 표본들이 16온스보다 크거나 같은 무게를 지녔다는 것을 의미합니다.
따라서 우리는 100개 중에서 95개 이상이 16온스보다 작아야 시리얼 회사가 주장하는 바와 달리 시리얼 무게는 평균 16온스보다 작을 것이라고 주장할 수 있는데, 그 주장을 할 근거가 부족하다는 것을 알 수 있습니다.
이번에는 양측검정(two-sided test)을 한 번 해보겠습니다. 이번에는 정확하게 16온스이냐 아니냐를 가지고 보겠습니다.
capt_test_results <-
t.test(capt_crisp$weight, mu = 16,
alternative = c("two.sided"), conf.level = 0.95)
capt_test_results
One Sample t-test
data: capt_crisp$weight
t = -1.2, df = 8, p-value = 0.2645
alternative hypothesis: true mean is not equal to 16
95 percent confidence interval:
15.70783 16.09217
sample estimates:
mean of x
15.9 양측검정은 신뢰구간을 다음과 같이 제시합니다.
capt_test_results$conf.int[1] 15.70783 16.09217
attr(,"conf.level")
[1] 0.95양측검정은 방향이 정해진 것이 아니다보니까 특정한 값, 여기서는 16온스죠, 그 값보다 음의 방향으로 다를 경우와 양의 방향으로 다를 경우를 모두 고려했을 때, 신뢰수준 5%의 검정을 하게 됩니다. 즉, 결정값(critical value)는 영가설의 값을 기준으로 음의 방향에서 2.5%, 양의 방향에서 2.5%에 대한 것이 됩니다. 결정값을 구하는 공식이 \(t_{n-1}(\alpha/2) = t_s(0.025)\)라고 할 때, R의 분위수를 구하는 qt()를 이용하면 다음과 같습니다.
qt(0.975, df = 8)[1] 2.306004시리얼 박스의 평균무게에 대한 95% 신뢰구간을 공식에 대입해서 구하면:
\[
x\pm t_{n-1}(\alpha/2)\frac{s}{\sqrt{n}}
\] 이므로 R로는
c(mean(capt_crisp$weight) -
qt(0.975, df = 8) * sd(capt_crisp$weight) / sqrt(9),
mean(capt_crisp$weight) +
qt(0.975, df = 8) * sd(capt_crisp$weight) / sqrt(9))[1] 15.70783 16.09217t.test()로 구한 결과와 동일하다는 것을 알 수 있습니다.
2표본 t-Test
\(x_i \sim \mathrm{N}(\mu_x, \sigma^2)\)라고 하고, \(y_i \sim \mathrm{N}(\mu_y, \sigma^2)\)라고 할 때, 우리는 2표본 검정을 위해 영가설을 \(H_0 :\mu_x - \mu_y = \mu_0\), 연구가설을 \(H_A:\mu_x-\mu_y\neq \mu_0\)이라고 수립할 수 있습니다.
\(\sigma\)를 알고 있다고 할 때, 2표본 스튜던트 \(t\) 검정통계량은 다음과 같이 구할 수 있습니다.
\[ t = \frac{(\bar{x}-\bar{y})-\mu_0}{s_p\sqrt{\frac{1}{n} + \frac{1}{m}}} \sim t_{n+m-2} \]
간단히 얘기하면 두 표본의 차이가 서로 다른 모집단에서 나와서 진짜로 다를 차이인지, 혹은 하나의 표본에서 나왔는데 표본추출의 문제로 인해 나타난 불확실성으로 인한 차이일지 구별하기 위한 것입니다.
위의 공식에서 \(\bar x= \frac{\sum^n_{i=1}x_i}{n}, \bar y = \frac{\sum^m_{i=1}x_i}{m}\)이고, \(s^2_p = \frac{(n-1)s^2_x + (m-1)s^2_y}{n+m-2}\)입니다.
이때, \(\mu_x-\mu_y\)에 대한 \(100(1-\alpha)\)%의 신뢰구간은 다음과 같이 계산할 수 있습니다.
\[ (\bar x - \bar y)\pm t_{n+m-2}(\alpha/2)\Bigg(s_p\sqrt{\frac{1}{n} + \frac{1}{m}}\Bigg) \]
그리고 이때, \(t_{n+m-2}(\alpha/2)\)는 \(\Pr(t>t_{n+m-2}(\alpha/2))=\alpha/2\)로 계산되는 결정값입니다.
2표본 t-Test: Example
\(X\)와 \(Y\)라는 두 표본이 각각 \(\mathrm{N}(\mu_1,\sigma^2)\)과 \(\mathrm{N}(\mu_2,\sigma^2)\)의 분포를 따른다고 할 때, 표본규모가 6인(\(n=6\))인 확률변수 \(X\)와 표본규모가 8인 확률변수 \(Y\)를 다음과 같이 얻었다고 하겠습니다.
x <- c(70, 82, 78, 74, 94, 82)
n <- length(x)
y <- c(64, 72, 60, 76, 72, 80, 84, 68)
m <- length(y)이때, 우리는 영가설을 \(H_0:\mu_1=\mu_2\), 대안가설이 \(H_A: \mu_1 > \mu_2\)라고 할 수 있습니다.
첫째, 표본평균과 표준편차를 구해보겠습니다.
x_bar <- mean(x)
s_x <- sd(x)
y_bar <- mean(y)
s_y <- sd(y)이때, 두 확률변수를 합쳤을 때의 표준편차는 다음과 같습니다.
\[ s_p = \sqrt{\frac{(n-1)s^2_x + (m-1)s^2_y}{n+m-2}} \]
당연히 R로 계산할 수 있습니다.
s_p <- sqrt(((n - 1) * s_x ^ 2 +
(m - 1) * s_y ^ 2) / (n + m - 2))그리고 이에 해당하는 \(t\) 검정통계량은 다음의 공식대로 구할 수 있습니다.
\[ t = \frac{(\bar x - \bar y)-\mu_0}{s_p\sqrt{\frac{1}{n} + \frac{1}{m}}} \]
t <- ((x_bar - y_bar) - 0) /
(s_p * sqrt(1 / n + 1 / m))
t[1] 1.823369\(t \sim t_{n+m-2} = t_{12}\)라고 할 때, \(p\)-값은 다음과 같이 계산할 수 있습니다.
\[ \Pr(t_{12} > 1.823369) \]
1 - pt(t, df = n + m - 2)[1] 0.04661961위의 전 과정은 t.test() 함수를 이용해 동일하게 구할 수 있습니다.
t.test(x, y, alternative = c("greater"), var.equal = TRUE)
Two Sample t-test
data: x and y
t = 1.8234, df = 12, p-value = 0.04662
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
0.1802451 Inf
sample estimates:
mean of x mean of y
80 72 두 확률변수 \(X\)와 \(Y\)를 데이터프레임으로 변환하여 분석할 수도 있습니다.
t_test_data <-
data.frame(values = c(x, y),
group = c(rep("A", length(x)),
rep("B", length(y))))
t_test_datavalues group 1 70 A 2 82 A 3 78 A 4 74 A 5 94 A 6 82 A 7 64 B 8 72 B 9 60 B 10 76 B 11 72 B 12 80 B 13 84 B 14 68 B
데이터프레임을 이용할 시에는 ~ 명령어를 이용해 프레임 안의 변수로 2표본 t.test()를 수애할 수 있습니다.
t.test(values ~ group, data = t_test_data,
alternative = c("greater"), var.equal = TRUE)
Two Sample t-test
data: values by group
t = 1.8234, df = 12, p-value = 0.04662
alternative hypothesis: true difference in means between group A and group B is greater than 0
95 percent confidence interval:
0.1802451 Inf
sample estimates:
mean in group A mean in group B
80 72 Footnotes
뒤의
rnorm()을 이용하여 무작위로 생성한 100개의 값을 구했기 때문에, 이 결과는 구할 때마다 달라질 것입니다.↩︎