# 패키지가 설치되어 있지 않을 시
install.packages("estimatr")
library(estimatr)
lm_robust(y ~ x1 + x2 + as.factor(year),
clusters = cluster_id,
data = sample)2 임의효과 모형
이 장에서는 \(y_{it} = X_{it}\beta + u_{it}\)라는 선형 패널모형의 해석과 추정에 대해서 살펴본다. 이때, \(X_{it}\)에는 흔히 상수항과 시간더미들이 포함된다. 상수항과 시간더미를 따로 표현하고 싶을 경우에는 \(y_{it} = \alpha + X_{it}\beta + \delta_t + u_{it}\)라고 쓸 수 있는데, 이때 더미변수의 특성으로 인해 \(\delta_1 = 0\)이라는 제약을 준다.1 시간더미들은 특별한 사유가 없는 한 포함시키는 것이 좋다.
패널 데이터가 주어지고 패널 모형이 설정되더라도 데이터가 패널 구조를 갖는다는 사실을 무시한 채 개체와 시간을 한 데 모아(pool) 보통최소제곱법(Ordinary Least Squares, OLS)로 모델을 추정할 수있다. 이 방법을 통합최소제곱법(Pooled OLS, POLS)라고 한다.
동일한 개체 내에서는 시간에 걸친 종속성이 존재할 수 있다. 즉, 한 개체에 대한 확률변수가 시간에 따라 변화할 수 있다는 것이다. 자연적으로 증가한다거나 감소하는 것을 생각해볼 수 있다. 이 경우에는 개체 내 오차항들 간 특별한 형태의 상관이 존재한다고 가정할 수 있다. 즉, 어떠한 변수가 시간에 따라 변화한다면 \(t\) 시점의 오차항은 \(t-1\) 시점의 변수와 관계가 있을 수 있다. 이 경우에는 이러한 상관을 가정한 일반화된 최소제곱(FGLS) 추정을 하는 방법이 있는데, 이를 임의효과(random effects, RE) 회귀 또는 RE FGLS 회귀라고 한다. 이 방법은 오차항이 시간불변항과 무작위 오차의 합으로 구성된다고 보는 오차성분(error components) 모형의 FGLS 추정법이다.
전통적으로 오차항이 시간불변 항(임의효과)과 무작위 오차(이분산·자기상관이 없음)로 구성되어 있다는 가정 하에서, 오차성분 모형에서 시간불변 항이 존재하는지 여부를 검정하는 경우가 있다. 만약 시간불변 항이 존재하지 않는다면 POLS가 BLUE일 것이므로 통상적인 분산추정에 무리가 없을 것이다. 2.5절은 이러한 검정에 관한 내용을 살펴본다. 2.6절에서는 오차항 구성 부분들이 정규분포를 갖는다는 가정 하에서 최우추정(maximum likelihood estimation, MLE) 방법을 살펴본다. MLE는 나중에 동태적 모형과 비선형 모형에서 중요한 분석도구가 된다.
모형은 각 시점의 횡단면 함수관계를 나타낼 수도 있고, 각 개체가 시간에 걸쳐 변화하는 방식을 나타내도록 설정할 수도 있다.
모집단평균(population averaged, PA) 모형: 횡단면 함수관계를 나타내는 모형
개체별(subject specific, SS) 모형: 개체별 시간에 따른 변화를 나타내는 모형
설명변수가 오차항에 대해 강외생적인 한(즉, 내생성의 문제가 존재하지 않는 한) 이 두 모형의 구분은 중요하지 않으며, 기울기 모수(\(\beta\))는 동일한 의미를 갖는다. 모집단평균 모형은 흔히 일반화된 추정식(GEE) 방법으로 추정한다.
2.1 선형 패널모형의 기초
선형모형은 다른 조건들이 일정할 때, 한 변수의 변화가 종속변수의 변화와 어떠한 관계를 보이는지를 살펴본다. 패널 데이터에서 종속변수를 \(y_{it}\)라 하고, 독립변수를 \(X_{it}\)라 하자. 가장 흔한 선형 패널모형은 \(y_{it} = X_{it}\beta + u_{it}\) 와 같다.
\(X_{it}\beta\) 는 \(\beta_1 X_{1,it} +\cdots +\beta_kX_{k,it}\) 를 축약하여 나타낸 것이다.
\(u_{it}\)는 \(y_{it}\)와 \(X_{it}\) 간의 선형함수 관계를 교란하는 오차항(error term) 혹은 교란항(disturbance term)이다.
통상적으로는 \(X_{it}\)에 상수항(constant term)과 시간더미들(time dummies)이 포함되기 때문에 경우에 따라서는 상수항과 시간더미들을 명시적으로 표현하여 모형을 다음과 같이 나타낼 수도 있다: \(y_{it} = X_{it}\beta + u_{it}\).
\(\alpha\)는 절편, 상수항이다.
\(\delta_t\)는 시간더미, 시간효과를 나타낸다. 각각의 \(\delta_t\)는 \(t\)기기에 해당하는 시간더미 변수들에 그 계수를 곱한 것이다.
시간더미들이 포함되어 있는 모형에서는 절편이 시간에 따라 변할 수 있다(\(\alpha\)와 \(\delta_t\)가 합해져서 절편이 되는 거니까). 대부분의 연구에서 시간더미들을 모형에 포함시킨다. 연구자가 재량 껏 시간더미들의 일부 혹은 전부를 모델에서 제거할 수도 있지만, 그 경우에는 이유를 잘 성명하여야 한다. 한치록 (2021, 24)에서 언급한 바와 같이 정치학에서 주로 다루는 교차사례 시계열 데이터는 개체의 수를 \(n\), 시간의 길이를 \(T\)라 할 때, 대체로 \(n > T\)인 경우가 많기 때문이다. 이런 경우에는 시간더미 면수들이 따름모수 문제를 야기하지 않는다.
Note
연습 2.1. 첨자에 주의를 기울인다면 시간더미들은 \(X_{1, it}\), \(X_{2,i}\), \(X_{3,t}\) 중 어디에 해당하겠는가?
Ans: 시간더미들은 시간에 따라 변화하는 것을 나타내므로 \(X_{3, t}\)로 표현할 수 있다.
\(y_{it} = \alpha + X_{it}\beta + \delta_t + u_{it}\)에서 \(\beta\)가가 무엇을 의미하는지 생각해보자. 이 경우 동일 시점에서 \(X_{it}\)에 \(\Delta x\)만큼 차이가 있는 두 개체의 종속변수에 \((\Delta x)\beta\) 만큼 차이가 있을 것으로 기대된다고 해석된다. 만약 상이한 시점 간 비교를 한다면 종속변수의 기댓값의 차이는 \((\Delta x)\beta\)와 시간대별 효과의 차이를 합한 값이 될 것이다.
\(y_{it} = X_{it}\beta + u_{it}\) 모형에서 한 가지 유의할 점은 \(\beta\)가 모든 \(i\)에서 동일하다는 사실이다. \(i\)가 국가를 나타낸다고 하면, 한 국가에서의 절편 및 기울기 계수가 다른 국가에서 절편 및 기울기 계수와 동일하다는 것이다.
Note
국가별로 계수가 모두 상이하다면, 각 국가별로 시계열 데이터를 분석하면 될 것이다. 패널 데이터를 사용하는 이유는 A국에서의 변수 간 관계를 구하기 위하여 B국의 데이터를 고려하기 위함이다. 단, 이 경우 국가별 관측치의 개수가 충분해야 제대로 된 추정을 할 수 있다. 예를 들어, 5개 연도 패널 데이터로써 \(\beta\)가 \(i\)마다 다른 모형을 제대로 추정할 수는 없다.
개체들을 몇 개의 군으로 나누어, \(\beta\) 계수가 모든 개체에서 상이하지는 않고 각 개체군 내에서는 동일하지만 상이한 개체군 간에는 상이하도록 설정할 수도 있다. 예를 들어, 기업들의 데이터가 있을 대, 동일 산업 내의 기업들은 동일한 \(\beta\)를 갖게 할 수 있다. 설명변수들과 산업 더미변수들의 상호작용(interaction) 항을 포함시키는 것과 동일하다.
\(\beta\) 계수가 모든 \(i\)에서 동일한지 검정할 수 있다. 이를 통합가능성(poolability) 검정이라고 한다.
-
국가의 수(\(n\))가 적고 기간(\(T\))이 긴 패널 데이터는 국가별 더미변수들 및 \(X_{it}\)와의 상호작용 항들을 포함시키고 나서 상호작용 항의 계수가 0인지를 간단히 검정해볼 수 있을 것이다.
- 이 경우, 국가의 수가 작기 때문에 국가별 더미와 설명변수 간의 상호작용항의 개수가 상대적으로 많지 않아 가능하며, 상호작용 항의 영가설이 0일 것을 기각한다면 설명변수가 종속변수에 미치는 영향이 국가에 따라 조건적일 것이라는 의미이므로 단순하게 통합하여 분석하기는 어려울 것이다.
-
계수가 국가마다 다름에도 불구하고 여러 국가들의 데이터를 모아서 분석을 한다면 여기에는 두 가지 이유가 있을 수 있다.
-
그렇게 함으로써 개별 회귀보다 더 효율적인 추정량을 얻을 수 있기 때문이다.
- 오차항이 국가 간에 상관된 경우에 해당하며, Zellner (1962) 의 SUR (seemingly unrelated regressions, 겉보기에는 상관없는 회귀들)을 이용하여 구현할 수 있다.
-
한 나라가 다른 나라에 미치는 직접적인 영향을 살펴보고 싶은 경우이다.
- 타국의 변수들을 포함하는 모형을 고려해볼 수 있다.
-
2.2 통합최소제곱 회귀
\(X_{it}\)를 독립변수들의 벡터, \(y_{it}\)를 종속변수, \(u_{it}\)를 오차라고 할 때, 본 장에서 고려할 모형은 모든 개체에서 \(\beta\)가 동일하도록 설정된 다음과 같은 모형이다.
\[\begin{equation} \label{eq-ch2-1} \tag{2.1} y_{it} = X_{it}\beta + u_{it} \end{equation}\]만약 절편이나 계수들이 \(t\)마다 다른데도 모형을 이렇게 간단히 표현하였다면, \(X_{it}\)라는 벡터 내에는 설명변수와 시간더미 간 상호작용항들이 포함되어 있다고 간주할 수 있다.
- 예를 들어, 종속변수가
y이고 설명변수가x1,x2이며, 절편과x1계수가 \(t\)마다 다르다면, \(X_{it}\)는1,x1,x2, 연도별 더미들,x1과 연도별 더미들의 상호작용함을 포함한다(R이라면x2x1*as.factor(year)). 한치록 (2021, 26)에서는 더미변수 함정(공선성)을 피하기 위해 한 해의 연도 더미는 제외시켜야 한다고 서술하고 있는데, 보통 패널 데이터 구조에서 연도 변수는 긴 형태(long type)으로 연도(year)라고 하는 변수에 값들이 입력되어 있기 때문에, R에서as.factor(year)로 입력하면 가장 작은 값을 디폴트로 준거집단으로 삼아 제외한다.
Note
연습 2.2. \(i\)가 국가, 종속변수는 환율, 설명변수는 유가와 고령인구비율이다. 환율이 고령인구비율에 반응하는 방식은 모든 국가에서 동일하나 환율이 유가에 반응하는 방식은 산유국과 비산유국 간에 상이할 수 있도록 하려면 모형을 어떻게 설정해야 하겠는가?
Ans: \(\mathrm{환율}_{it}\) ~ \(f(\mathrm{고령인구비율}_{t}, \mathrm{유가}_{it}\times I(\mathrm{산유국 = 1}))\)
이 경우에는 산유국과 비산유국을 식별할 수 있는 더미변수가 추가적으로 필요할 것이다.
패널 데이터를 분석할 때에는 일반적으로 \(u_it\)가 \(i\)에 걸쳐 서로 독립이라고 가정한다. 즉, 서로 다른 개체들은 독립적으로 행동한다는 것이다. 그러나 패널에서 \(u_{it}\)가 \(t\)에 걸쳐 독립이라 보기는 어렵다. 생각해보면 당연하다. 동일한 개체의 비관측 요소인 \(u_{it}\)가 시간에 걸쳐 상관되기 쉽기 때문이다. 오차항의 시기에 걸친 상관은 ♖와 관련된 문제이다.
책에서는 문제를 단순화하기 위해 일단은 모든 \(i\)에서 \(T_i\)가 동일하다고 하고, 특별한 경우가 아니면 균형패널만을 고려한다.
모형 \(\ref{eq-ch2-1}\)에서 한 가지 유의할 점은 \(\beta\)는 모든 개체와 시점에서 동일하다는 것이다. 계수가 \(\beta_{it}\)라면 임의계수 모형이 되며, 이때 분석의 목적은 \(\beta_{it}\)의 값들이 아니라 이 값들의 분포를 알아내는 것이 된다.
Warning
\(n\)이 크고 \(T\)가 작은 경우에 계수가 \(i\)마다 다르면 따름모수 문제가 발생할 수 있다. \(n\)이 작고 \(T\)가 큰 패널 데이터의 경우에는 시간더미가 문제를 야기한다 (한치록 2021: 27).
모형 \(\ref{eq-ch2-1}\)에서 설명변수(\(X_{it}\))와 오차(\(u_{it}\))가 서로 독립이라고 가정하고 \(\beta\)를 추정해 볼 수 있다. 이 가정이 일단은 맞다고 할 때, OLS 방법을 생각해볼 수 있다. 이 경우는 여러 시점의 데이터들을 통합하는 것이므로 통합 OLS, POLS라고 할 수 있다. 횡단면 데이터의 경우와 마찬가지로 만약 모든 \(i\)와 \(t\)에서 \(\mathrm{E}(u_{it}|\mathbb{X}) = 0\)이면 POLS는 비편향이다.2 당연하다. 통합한 각 관측치들이 모두 서로 독립적이라고 가정한 것이므로 교차사례 시계열적 구조를 가지고만 있을 뿐이지 사실상 교차사례 데이터와 다를 것이 없기 때문이다.
POLS 추정량을 식으로 표현하면 다음과 같다. \(X_{it}\)가 상수항과 시간더미들을 포함한 모든 설명변수들의 행벡터(\(1\times k\))라 하자. 그러면 POLS 추정량은 다음과 같다.
\[\begin{equation} \label{eq-ch2-2} \tag{2.2} \hat{\beta}_{pols} = \left(\sum^{n}_{i=1}\sum^{T}_{t-1}X^{\prime}_{it}X_{it}\right)^{-1} \sum^{n}_{i=1}\sum^{T}_{t-1} X^{\prime}_{it}y_{it} \end{equation}\]이 추정량은 절편과 시간더미 계수 추정량들을 모두 포함하고 있으며, 결국 모든 관측치들을 이용하여 OLS를 한 형태라는 것을 알 수 있다. 원서에서는 이 식을 유도하여 POLS 추정량이 시기별 횡단면 함수관계 추정치 벡터들의 가중평균이라는 것을 보여준다. 즉, 시점별로 교차사례들의 OLS를 구한 뒤, 추정된 \(\hat{\beta}\)들을 시점(\(t\))을 이용해 가중치를 부여, 가중평균을 구한 것이다.
서로 다른 개체 간 오차항이 독립이라고 보는 것은 그렇게 나쁘지 않지만 동일 개체 내에서 오차항이 시간에 걸쳐 독립이라고 보는 것은 무리이다. 모형 \(\ref{eq-ch2-1}\)의 \(X_{it}\beta\)가 종속변수 \(y_{it}\)에 존재하는 시계열 상관을 완벽하게 설명한다고 보기 어렵기 때문이다. 이처럼 오차항의 시계열 상관을 의심할 때, POLS를 이용해 올바른 추론을 하려면 클러스터 분산추정량을 사용할 수 있다(♖). R에서는 여러 가지 방법을 통해 클러스터 분산추정량을 사용할 수 있는데, 여기에서는 estimatr 패키지의 lm_robust() 함수를 사용한다.
클러스터 표준오차를 사용할 때 중요한 점은 클러스터의 개수가 많아야 한다는 것이다. 클러스터의 개수가 작을 경우에 클러스터 표준오차를 사용할 경우, 계산된 값들을 신뢰하기 어려울 것이다.
Note
예제 2.1. 임금 방정식
klipsbal.dta 데이터는 2005년부터 2015년까지 한국노동패널로부터 전체 기간에 고용되어 양의 임금을 받은 개인들을 추출하여 만든 균형패널 데이터이다. 임금(로그)이 교육수준, 근속연수, 정규직 여부, 성별, 연령(2005년도 연령)에 의하여 어떠한 영향을 받는지 살펴보고자 한다. 연도별 더미를 포함하여 공통의 연도별 변화를 제거할 것이다.
library(estimatr) # 클러스터 표준오차 추정을 위한 패키지
library(ezpickr) # 데이터를 불러오기 위한 패키지
library(tidyverse) # 데이터 관리를 위한 패키지
library(texreg) # 분석 결과를 보여주기 위한 패키지
klipsbal <- pick("http://econ.korea.ac.kr/~chirokhan/panelbook/data/klipsbal.dta")
re_cluster <- lm_robust(lwage ~ educ + tenure + I(tenure^2) + isregul +
female + age05 + I(age05^2) + as.factor(year),
clusters = pid,
data = klipsbal)
re_cluster |> screenreg(digits = 4, include.ci = FALSE, single.row = TRUE,
include.rsquared = TRUE, include.adjrs = TRUE)
===========================================
Model 1
-------------------------------------------
(Intercept) 2.9839 (0.1963) ***
educ 0.0562 (0.0047) ***
tenure 0.0332 (0.0041) ***
tenure^2 -0.0004 (0.0002) **
isregul 0.2717 (0.0275) ***
female -0.3892 (0.0247) ***
age05 0.0651 (0.0088) ***
age05^2 -0.0009 (0.0001) ***
as.factor(year)2006 0.0525 (0.0097) ***
as.factor(year)2007 0.0973 (0.0106) ***
as.factor(year)2008 0.1421 (0.0109) ***
as.factor(year)2009 0.1450 (0.0121) ***
as.factor(year)2010 0.1891 (0.0131) ***
as.factor(year)2011 0.2323 (0.0140) ***
as.factor(year)2012 0.2695 (0.0149) ***
as.factor(year)2013 0.3050 (0.0153) ***
as.factor(year)2014 0.3131 (0.0164) ***
as.factor(year)2015 0.3398 (0.0180) ***
-------------------------------------------
R^2 0.5970
Adj. R^2 0.5963
Num. obs. 9196
RMSE 0.3683
N Clusters 836
===========================================
*** p < 0.001; ** p < 0.01; * p < 0.05일반적으로 분석결과를 보고하듯 출력하기 위해 texreg 패키지를 이용하였다. 클러스터 표준오차를 사용한 POLS 추정인데, 여기서 lm_robust() 함수의 clusters = pid 옵션이 STATA에서의 vce(cl pid) 옵션과 같다고 보면 된다.
원서에서와 마찬가지로 연도별 공통의 변화, 근속연수, 정규직 여부, 성별, 연령을 통제할 때 1년 교육(educ)은 임금을 약 0.06% 상승시키는 것으로 추정된다. 또한 여타 변인들과 연도별 효과를 통제할 때, 정규직은 비교가능한 비정규직에 비하여(isregul) 임금이 약 0% 높다. female 변수의 계수도 유사하게 해석할 수 있다. tenure는 임금을 증가시키는 효과를 갖지만 그 정도는 점점 줄어든다. age05 효과의 반환점—즉 효과가 증가하다가 감소하는 지점은 1차항인 age05의 계수값 통해 살펴볼 수 있다. \(\frac{1}{2}\times \mathrm{age05}/\mathrm{age05^2}\)으로 계산할 수 있는데, 그 결과값은 37으로, 2005년도의 나이가 약 37세 이하인 경우에는 나이가 많을수록 임금이 높지만 그 이후에는 나이가 많을수록 임금이 낮은 것으로 추정된다. 연도 더미의 계수값은 2005년에 비해 최근으로 올수록 증가하는데, 이는 다른 요인들을 통제했을 때, 해가 갈수록 임금 수준이 전반적으로 높아지는 것을 의미한다.
POLS 결과로부터 인과관계를 추론하기 위해서는 오차항이 설명변수와 상관이 없다는 조건이 필요하다. 이를 위해서는 오차항에 포함되어 있을 수 있는 누락된 요인들 중에 설명변수들과 관련된 것이 없어야 한다. 만약 설명변수 및 종속변수와 관계가 있을 수 있는 변수를 모델에 포함하지 않았을 경우에는 누락변수로 인한 편향이 있을 수 있어서, 다른 조건이 동일할 때라는 서술이 어렵다.
Note
예제 2.2. 인구구조와 총저축
wdi5bal.dta 데이터는 세계은행(World Bank)의 World Development Indicators (WDI) 자료 중 신생아 기대여명(lifeexp), 총저축율(sav), GDP 대비 경상수지 비율(ca) 데이터를 추출하고 여기에 UN의 인구자료를 추가하여 만든 것이다. 연습용 예제로 산유국을 제외한 96개국에 대하여 균형패널 데이터를 만든 것이다. 인구 구조는 총 인구 중 연령대별 비중을 0-19세, 20-29세, 30-64세, 65세 이상으로 나눈 것이다. 인구 비중들은 백분율(%)로 표현한 것이다.
WDI자료는 연간이고 UN 인구자료는 5년 단위이므로 UN 인구자료에 대해 줄긋기(interpolation)를 하여 연도별 데이터를 만들거나, 반대로 총저축률과 경상수지 자료에 대하여 앞뒤 2년씩을 포함한 5년 평균을 구해 5년 간격 데이터를 만들 수 있다. wdi5bal.dta 데이터는 5년 평균 자료를 만든 것이다. 최종적으로 만들어진 자료는 1985년부터 2010년까지 5년 간격의 패널 데이터이며, 산유국을 제외하고 모든 연도의 자료가 있는 국가들만을 포함한다. 결과적으로 \(n = 96\), \(T = 6\)의 균형패널 데이터이다.
이 데이터를 이용하여 총저축율(sav)을 인구 구조(age0_19, age20_29, age65over)와 신생아 기대수명(lifeexp)에 대해 회귀해 보자. 장년층 비율(age30_64)를 제외하였으므로 인구 구조 더미변수의 결과들은 장년층 비율에 비교하여 해석할 수 있다.
wdi5bal <- pick("http://econ.korea.ac.kr/~chirokhan/panelbook/data/wdi5bal.dta")
re_cluster2 <- lm_robust(sav ~ age0_19 + age20_29 + age65over + lifeexp +
as.factor(year),
clusters = id, data = wdi5bal)
re_cluster2 |> screenreg(digits = 4, include.ci = FALSE, single.row = TRUE,
include.rsquared = TRUE, include.adjrs = TRUE)
===========================================
Model 1
-------------------------------------------
(Intercept) 44.0451 (16.3279) *
age0_19 -0.6947 (0.1892) ***
age20_29 -0.3529 (0.4336)
age65over -1.4151 (0.4968) **
lifeexp 0.2245 (0.1042) *
as.factor(year)1990 0.3150 (0.7518)
as.factor(year)1995 -0.3435 (0.8512)
as.factor(year)2000 -1.5042 (0.8419)
as.factor(year)2005 -0.9562 (1.0082)
as.factor(year)2010 -2.8367 (1.1912) *
-------------------------------------------
R^2 0.2453
Adj. R^2 0.2333
Num. obs. 576
RMSE 8.5640
N Clusters 96
===========================================
*** p < 0.001; ** p < 0.01; * p < 0.05클러스터 표준오차 옵션을 통해 \(u_{it}\) 내의 시계열 상관을 고려한 표준오차 추정이 가능하다. 분석 결과, 0-19세 인구의 비율이 높을수록 총저축률이 낮은 경향이 관측된다. 65세 이상 인구의 비율이 높을수록 저축률이 낮으며, 30-64세 대신 65세 이상 인구 비율이 1%p 높으면 저축율을 1.4%p 낮은 것으로 추정된다. 19세 이하나 65세 이상 인구 비율이 높으면 사회 전체가 이들을 부양하여야 하므로 소비 비중이 증가하고 저축 비중이 하락하는 것은 자연스러워 보인다.
연령대별 인구 비율이 동일할 때, 신생아의 기대수명이 1년 높으면 총저축률은 0.2%p 높은 것으로 추정된다. 기대수명이 늘어날수록 구성원들은 더 오랜 기간 소비하며 살아가야 하므로 저축률이 증가하는 것으로 일견 해석할 수 있지만, 이 계수 자체의 해석에는 조심할 필요가 있다. 신생아 기대수명이 증가할 경우 고령층 인구 비율이 늘어나는 것이 상식적으로 보이는데 모형에서는 연령대별 인구 비율이 통제되어 있다. 결국, lifeexp의 계수는 기대수명이 1세 늘어나면서 동시에 출산율이 딱 맞게 조정되어 19세 이하, 20-29세, 30-64세,65세 이상 인구의 비율이 동일하게 유지되는 경우 총저축률이 받는 영향을 의미하기 때문이다.
시간더미의 계수값들을 보면, 인구구조와 기대수명의 변화로써 설명할 수 없는 연도별 저축률 하락을 관측할 수 있다. 단, 1985년과 비교해 2010년의 값만이 통계적으로 유의미하다.
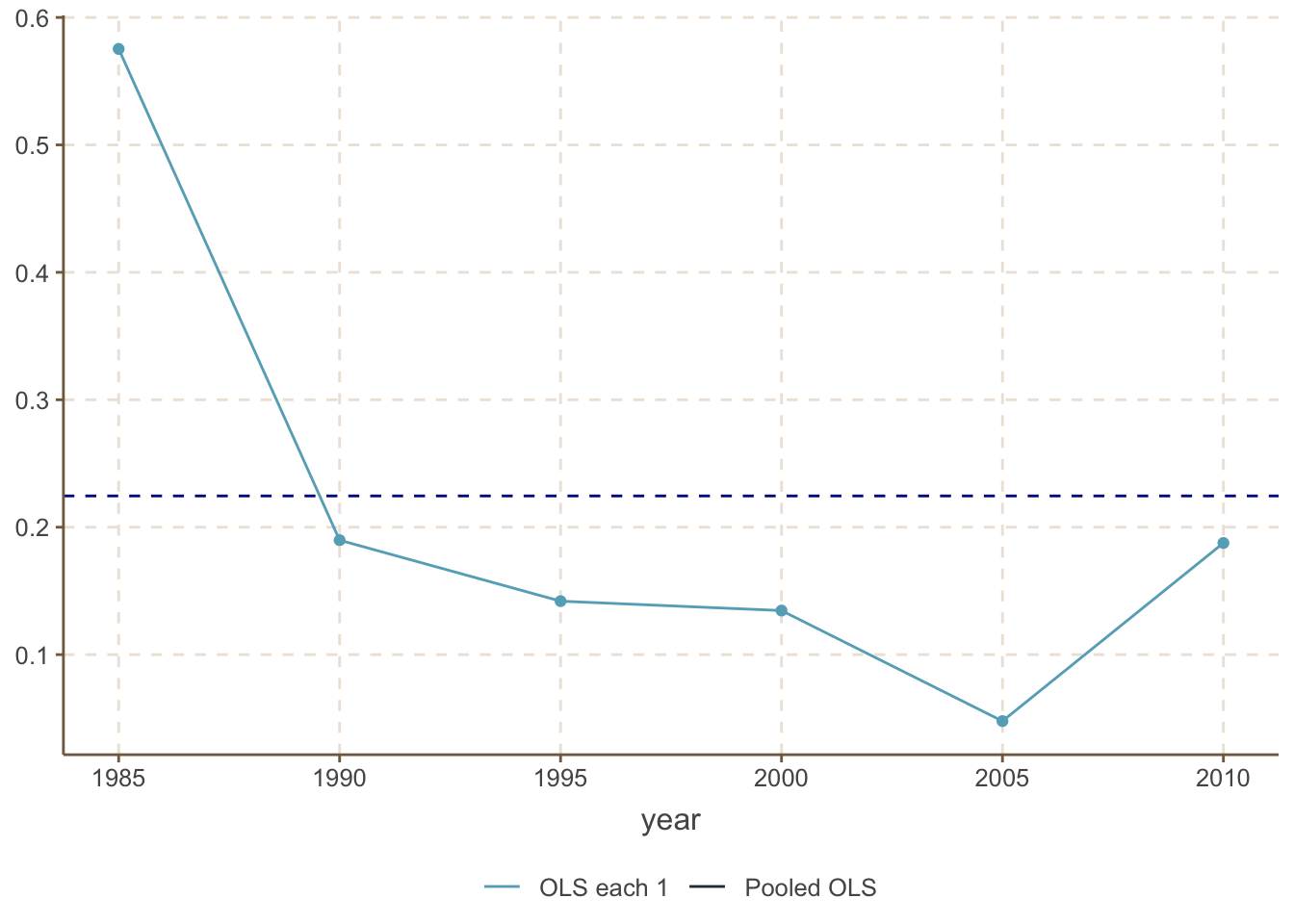
앞에서 POLS 추정값은 각 \(t\)별 OLS 추정값들의 가중평균이라고 하였는데, 실제로 위의 데이터를 통하여 각 \(t\)의 OLS 계수들을 추정하여 보았다. lifeexp에 대하여 \(t\)별 OLS의 계수들과 POLS 계수를 비교하면 그림 \(\ref{figure2}\)와 같다.
만약 오차 \(u_{it}\)가 \(i\)에 걸쳐서 독립적이고 \(t\)에 걸쳐서도 독립적이라면 클러스터 표준오차가 아니라 이분산에 견고한(HC) 표준오차를 사용할 수 있다. 이 경우, se_type = HC1 옵션을 이용하여 설정할 수 있다. 이 HC 표준오차는 \(nT\)가 크기만 하면 좋은 성질을 가지고, 클러스터 표준오차는 \(n\)이 커야만 좋은 성질을 가진다. 따라서 \(n\)이 작지만 \(T\)가 커서 \(nT\)가 충분히 큰 상황이라면 HC 표준오차를 사용할 이유는 충분히 있다.
하지만 오차항들이 동일한 개체의 시간에 걸친 비관측 요소일 경우, 이들이 서로 독립적이라고 보기에는 무리가 있다.
만약 오차항이 \(u_{it} = \mu_i + \varepsilon_{it}\)의 구조를 가져서 모든 시점에 \(u_i\)가 공통으로 포함된다면, 거의 항상 시계열 상관을 가지므로 실제 분석에서 시계열 상관이 없다는 가정 하에서 이분산에만 견고한(HC) 표준오차를 사용하는 경우는 거의 없다.
만약 상이한 개체(\(i\))들일지라도 동일한 시간대에 상관관계가 존재한다면(시험볼 때 정보를 공유하는 것) 2중 클러스터(two way clustering) 방법을 사용하여 표준오차를 구할 수 있다.
\(n\)이 작으면 개체별 클러스터 방법이 문제를 야기할 수 있다.
\(T\)가 작으면 시간대별 클러스터 방법이 문제를 야기할 수 있다.
-
따라서 2중 클러스터 방법은 \(n\)도 크고 \(T\)도 커야만 잘 작동하는 방법이다.
\(\hat{V}_{id}\):
id에 따라 클러스터화한 분산추정값\(\hat{V}_{year}\):
year에 따라 클러스터화한 분산추정값\(\hat{V}_{id, year}\):
id와year의 값이 모두 동일한 것을 하나의 클러스터로 간주하는 클러스터 분산추정값(HC 분산추정값)공식에 따르면 \(\hat{V}_{2way} = \hat{V}_{id} + \hat{V}_{year} - \hat{V}_{id, year}\) 으로 표현할 수 있다 (Thompson 2011; Cameron and Miller 2015).
원서에서는 해당 내용에 대해서 지면을 할애하여 STATA 코드와 함께 보여주는데, 여기서는 그 내용은 생략하고 예제의 마지막, STATA에서 reghdfe를 사용한 부분만을 재현해보도록 한다.
twowaycl <- pick("http://econ.korea.ac.kr/~chirokhan/panelbook/data/twowaycl.dta")
library(sandwich)
library(lmtest)
model_twoway <- lm(y ~ x1 + x2 + after, data = twowaycl)
twoway_robust<- coeftest(model_twoway, vcov = vcovCL, cluster = ~ id + year)
twoway_robust |> screenreg(digits = 4)
========================
Model 1
------------------------
(Intercept) 0.9179 *
(0.3820)
x1 0.6795 ***
(0.0532)
x2 0.0829 ***
(0.0222)
after 0.5407
(0.5968)
========================
*** p < 0.001; ** p < 0.01; * p < 0.05POLS 추정을 위한 모형을 한 마디로 표현하면 각각의 \(t\)에서 \(\mathrm{E}(y_{it}|X_{it}) = X_{it}\beta\)라는 것이다. 이 모형은 한 개체 내에서 종속변수가 어떠한 방식으로 시간에 걸쳐 연관되느냐를 표현하는 것이 아니라 각 \(t\)에서 개체들의 모집단이 어떠한 패턴을 보이는지를 표현하는 것으로서 모집단 평균(population-averaged, PA) 모형에 해당한다.
Tip
패널 모형에서 PA 모형이란 종속변수가 \(t\)에 걸쳐 의존성을 보이는 현상을 무시하고 오직 각 시점에서 횡단면에 걸쳐 존재하는 관계를 표현해 주는 모형이다. 선형 PA 모형은 각 시점에서 종속변수와 설명변수 간에 평균적으로 존재하는 함수관계를 표현하며, 종속변수 내에 내재하는 시간에 걸친 종속성에는 관심을 두지 않는다. (한치록 2021: 41).
2.3 임의효과 모형
오차 \(u_{it}\)가 \(X_{it}\)와 상관되지 않는다고 가정하는 경우를 생각해보자. \(u_{it}\)에 개체에 걸친 상관은 없고 시계열 상관이 있는 경우를 고려해보자. 이 경우 오차항의 시계열 상관으로 인하여 POLS 추정량은 효율적이지 않다(♖). 더 효율적인 추정을 위하여 \(u_{it}\)의 분산·공분산 구조에 대하여 하나의 가정을 해 보자. 패널 모형에서 가정 널리 사용되는 가정은 \(u_{it}\)가 다음과 같이 두 성분으로 이루어졌다고 보는 것이다(오차성분 모형).
\[\begin{equation} \label{eq-ch2-6} \tag{2.6} u_{it} = \mu_i + \varepsilon_{it} \end{equation}\]식 \(\ref{eq-ch2-6}\)에서
\(\mu_i\)는 시간에 걸쳐 변화하지 않는 개별효과(individual effects); 국가에 따라 나타나는 오차
\(\varepsilon_{it}\)는 시간과 교차사례에 걸쳐서 변화하는 고유오차(idiosyncratic errors); 국가나 연도에 따라서 확인할 수 있는 오차
\(u_{it}\)는 오차 또는 총오차
모형 \(\ref{eq-ch2-6}\)이 주어질 때, 모형 \(\ref{eq-ch2-1}\)의 설명변수가 오차항과 무관하기 위해서는 개별효과와 고유오차 모두와 무관하여야 할 것이다. 이중 개별효과인 \(\mu_i\)는 설명변수와 상관되어 있는지에 따라 별도의 이름이 붙어있는데, 관측되는 속성인 (\(X_{i1}, \dots, X_{iT}\))와 무관하게 임의로 주어지는 효과인 \(\mu_i\)를 임의효과(random effects)라 하며, (\(X_{i1}, \dots, X_{iT}\))와 상관될 수 있는 개별효과를 고정효과(fixed effects)라고 한다.
- 간단하게 생각해보면, 국가-연도 자료를 분석할 때 국가들의 특정한 속성이 설명변수와는 무관한—확률적인 효과라고 한다면, 이를 임의효과라 할 수 있다. 반면에, 설명변수들이 어떤 국가냐에 따라서 영향을 받는다—개별효과가 설명변수와 상관된다면 이는 고정효과라 할 수 있다.
선형 임의효과 모형이란 오차항을 개별효과(\(\mu_i\))와 고유오차(\(\varepsilon_{it}\))의 합으로 두고, 설명변수(\(X_{it}\))는 고유오차(\(\varepsilon_{it}\))에 대하여 강외생적이고 개별효과(\(\mu_i\))는 임의효과라 가정하는 선형 모형을 말한다.
\(y_{it} = X_{it}\beta + \mu_i + \varepsilon_{it}\)
뒤의 3장의 선형 고정효과 모형은 \(\mu_i\)가 임의효과라는 가정을 하지 않는다.
2.4 임의효과 회귀
오차성분 모형 \(\ref{eq-ch2-6}\)이 맞다고 할 때, POLS 추정량이 일관성을 갖기 위해서는 \(\mu_i\)가 모든 \(X_{it}\)와 비상관이고 또한 모든 \(t\)에서 \(\varepsilon_{it}\)와 \(X_{it}\)가 비상관이면 된다.즉, 교차사례들을 시계열적으로 반복측정하여 얻은 데이터지만 개별 개체들의 개별효과가 설명변수와 독립적이고, 오차항 역시 독립적이면 된다는 얘기다. 반면, 임의효과 회귀가 일관적인 추정량을 제공하기 위해서는 \(X_{it}\)가 \(\mu_i\)에 대하여 외생적이면서 \(\mu_i\)에에 대하여 강외생적(strictly exogenous)이어야 한다. 즉, 모든 \(s\)와 \(t\)에서 \(X_{is}\)와 \(\varepsilon_{it}\)가 서로 비상관이어야 한다.3 이 경우, 동시기에 설명변수와 오차항이 서로 비상관일 뿐 아니라, 과거에서 온 충격(\(\varepsilon_{it-1}\) 등)도 현재의 설명변수(\(X_{it}\))에 영향을 미쳐서는 안 된다. 물론 \(X_{it}\)가 \(\mu_i\)에 대하여 외생적이라는 조건은 여전히 필요하다. 본 절에서는 설명변수 강외생성이 성립한다고 가정한다.
| 기호 | \(u_{it}\) | \(\mu_i\) | \(\varepsilon_{it}\) |
|---|---|---|---|
| 이름 | 오차 또는 총오차 | 개별효과 | 고유오차 |
\(u_{it}=\mu_i+\varepsilon_{it}\)일 때 이름들
임의효과 모형에서는 개별오차 \(\mu_i\)의 존재로 인하여 오차항에 시계열 상관이 존재하고, 이로 인하여 POLS는 더 이상 BLUE가 아니다(♖). 임의효과 모형에서 POLS보다 더 효율적인 추정을 하려면 \(\mu_i\)와 \(\varepsilon_{it}\)에 대한 명시적인 가정을 해야 한다.
- 한 가지 통용되는 가정은 \(\mu_i\)와 \(\varepsilon_{it}\)가 서로 비상관이고, \(\mu_i\)가 \(i\)에 걸쳐 동일한 분산을 가지며, \(\varepsilon_{it}\)가 \(i\)와 \(t\)에 걸쳐서 비상관이며 등분산 적이라는 것이다. 이 가정 하에서 총 오차의 분산과 공분산은 다음의 구조를 갖는다.
이 가정을 앞으로 오차 공분산 구조에 관한 임의효과 가정 또는 임의효과(RE) 공분산 가정이라 할 것이다. 전통적인 오차성분 모형은 이 RE 공분산 가정이 성립한다고 본다. RE 가정 \(\ref{eq-ch2-7}\)이 의미하는 바는 다음과 같다.
오차항(\(u_{it}\))의 분산이 \(\sigma^2_{\mu} + \sigma^2_{\varepsilon}\)으로 모든 \(i\)와 \(t\)에서 동일하다.
동일 개체 내 상이한 시점 간 오차들의 공분산이 \(\sigma^2_{\mu}\)으로 모두 동일하다.
상이한 개체 간에는 오차 공분산이 0이다.
이 가정 하에서 오차항은 등분산적이지만 특별한 형태의 자기상관을 갖는다.
Note
개별효과 \(\mu_i\)가 임의효과라고 할 때, 임의효과는 설명변수의 수준과 무관하게 무작위로 주어지는 개별효과 \(\mu_i\)를 말한다. 패널 임의효과 모형이란 개별효과가 임의효과라는 제약을 가한 패널 모형을 말한다. 오차 공분산 구조에 대한 임의효과 가정은 \(\ref{eq-ch2-7}\)의 가정을 말한다 (한치록 2021: 43).
RE 공분산 가정 \(\ref{eq-ch2-7}\) 하에서는 \(u_{it}\)에서 시간 순서를 뒤바꾸어 \(t=1\)과 \(t=2\)의 순서를 맞바꾸어도 공분산의 구조에 변화가 없다. 이런 공분산 구조를 교환가능(exchangeable)하다고 한다. 반면, 만약 서로 다른 시점의 고유오차 \(\varepsilon_{it}\)에 상관이 존재하면 일반적으로 \(\mathrm{cov}(\varepsilon_{i1}, \varepsilon_{i2})\)와 \(\mathrm{cov}(\varepsilon_{i1}, \varepsilon_{i3})\)이 상이하여 \(\mathrm{cov}(\varepsilon_{i1}, \varepsilon_{i2})\)와 \(\mathrm{cov}(\varepsilon_{i1}, \varepsilon_{i3})\)도 상이하므로 공분산 구조가 교환가능하지 않다. 이제 이 가정이 맞다는 전제 하에서 효율적인 추정량을 도출하는 것이 목적이다.
RE 공분산 가정 \(\ref{eq-ch2-7}\) 하에서, 만약 \(\sigma^2_{\mu}\)과 \(\sigma^2_{\varepsilon}\)을 안다면 오차항의 분산과 공분산을 완전히 알게 되므로 GLS 추정을 할 수 있다. 이 두 분산을 모르면 이들을 적절히 추정하여 FGLS를 할 수 있다. 이 FGLS를 임의효과(RE) 회귀(random effects regression)라 하고 그 추정량을 흔히 임의효과(Random Effects, RE) 추정량, 또는 RE FGLS 추정량이라 한다.
RE 회귀 분석을 위해 R을 사용하는 방법을 살펴보자.
POLS 시의 lm_robust 대신에 plm 패키지의 plm 함수를 사용하고 model = "random"이라는 옵션을 설정한다. 시간더미들은 as.factor(year)로 포함하였다.
Note
예제 2.4 임금방정식의 RE 회귀
예제 2.1의 모형과 데이터에 대하여 RE 추정을 해 보자.
klipsbal <- pick("http://econ.korea.ac.kr/~chirokhan/panelbook/data/klipsbal.dta")
model_random <- plm::plm(lwage ~ educ + tenure + I(tenure^2) + isregul + female +
age05 + I(age05^2) + as.factor(year),
data = klipsbal, model = "random",
index = c("pid", "year"))
summary(model_random)Oneway (individual) effect Random Effect Model
(Swamy-Arora's transformation)
Call:
plm::plm(formula = lwage ~ educ + tenure + I(tenure^2) + isregul +
female + age05 + I(age05^2) + as.factor(year), data = klipsbal,
model = "random", index = c("pid", "year"))
Balanced Panel: n = 836, T = 11, N = 9196
Effects:
var std.dev share
idiosyncratic 0.04553 0.21339 0.346
individual 0.08621 0.29362 0.654
theta: 0.786
Residuals:
Min. 1st Qu. Median 3rd Qu. Max.
-2.1487441 -0.1106801 0.0092481 0.1242738 2.2465048
Coefficients:
Estimate Std. Error z-value Pr(>|z|)
(Intercept) 2.7510e+00 1.8977e-01 14.4967 < 2.2e-16 ***
educ 6.7531e-02 3.9954e-03 16.9021 < 2.2e-16 ***
tenure 1.5389e-02 1.3481e-03 11.4155 < 2.2e-16 ***
I(tenure^2) -2.6591e-04 4.3035e-05 -6.1788 6.457e-10 ***
isregul 1.4590e-01 1.0244e-02 14.2433 < 2.2e-16 ***
female -4.1587e-01 2.3598e-02 -17.6228 < 2.2e-16 ***
age05 7.7436e-02 8.7848e-03 8.8148 < 2.2e-16 ***
I(age05^2) -9.9785e-04 1.0452e-04 -9.5474 < 2.2e-16 ***
as.factor(year)2006 6.1037e-02 1.0569e-02 5.7752 7.688e-09 ***
as.factor(year)2007 1.1898e-01 1.0621e-02 11.2020 < 2.2e-16 ***
as.factor(year)2008 1.7595e-01 1.0695e-02 16.4509 < 2.2e-16 ***
as.factor(year)2009 1.8711e-01 1.0799e-02 17.3273 < 2.2e-16 ***
as.factor(year)2010 2.3773e-01 1.0913e-02 21.7842 < 2.2e-16 ***
as.factor(year)2011 2.9077e-01 1.1087e-02 26.2257 < 2.2e-16 ***
as.factor(year)2012 3.3344e-01 1.1206e-02 29.7567 < 2.2e-16 ***
as.factor(year)2013 3.7969e-01 1.1413e-02 33.2673 < 2.2e-16 ***
as.factor(year)2014 3.9689e-01 1.1657e-02 34.0468 < 2.2e-16 ***
as.factor(year)2015 4.2889e-01 1.1863e-02 36.1524 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Total Sum of Squares: 723.58
Residual Sum of Squares: 427.29
R-Squared: 0.40947
Adj. R-Squared: 0.40838
Chisq: 6364.01 on 17 DF, p-value: < 2.22e-16model_random |> screenreg(digits = 4, include.ci = FALSE, single.row = TRUE,
include.rsquared = TRUE, include.adjrs = TRUE)
===========================================
Model 1
-------------------------------------------
(Intercept) 2.7510 (0.1898) ***
educ 0.0675 (0.0040) ***
tenure 0.0154 (0.0013) ***
tenure^2 -0.0003 (0.0000) ***
isregul 0.1459 (0.0102) ***
female -0.4159 (0.0236) ***
age05 0.0774 (0.0088) ***
age05^2 -0.0010 (0.0001) ***
as.factor(year)2006 0.0610 (0.0106) ***
as.factor(year)2007 0.1190 (0.0106) ***
as.factor(year)2008 0.1759 (0.0107) ***
as.factor(year)2009 0.1871 (0.0108) ***
as.factor(year)2010 0.2377 (0.0109) ***
as.factor(year)2011 0.2908 (0.0111) ***
as.factor(year)2012 0.3334 (0.0112) ***
as.factor(year)2013 0.3797 (0.0114) ***
as.factor(year)2014 0.3969 (0.0117) ***
as.factor(year)2015 0.4289 (0.0119) ***
-------------------------------------------
s_idios 0.2134
s_id 0.2936
R^2 0.4095
Adj. R^2 0.4084
Num. obs. 9196
===========================================
*** p < 0.001; ** p < 0.01; * p < 0.05기초 함수 중 하나인 summary()를 사용하면 좀 더 자세한 정보를 얻을 수 있다. 균형패널 데이터에 대한 분석이며 86개 개체의 11개 시점에 대한 데이터, 총 9,196개 관측치가 데이터에 존재한다는 것을 확인할 수 있다. 원서에 나와 있는 STATA 상의 sigma_u는 individual의 std.dev 값으로 \(\hat{\sigma}_\mu\)와 같고, sigma_e는 idiosyncratic의 std.dev 값으로 \(\hat{\sigma}_\varepsilon\)과 같다. STATA에서 제시된 rho는 \(\hat{\sigma}^2_\mu/(\hat{\sigma}^2_\mu + \hat{\sigma}^2_\varepsilon)\)로, 0.6544가 된다.
결과를 보면 예제 2.1.의 POLS 회귀 결과와 다른 점은 정규직 여부(isregul)의 계수값이 0.2716956이었는데, RE 추정값은 0.1459042으로 상당한 차이가 있다.
Note
연습 2.3. \(\hat{\sigma}_\mu\)와 \(\hat{\sigma}_\varepsilon\)로 rho를 계산하라.
Ans:
model_random$ercomp # 결과 확인 var std.dev share
idiosyncratic 0.04553 0.21339 0.346
individual 0.08621 0.29362 0.654
theta: 0.786round(0.29362^2/(0.29362^2 + 0.21339^2), 4)[1] 0.6544RE 회귀가 추정값을 어떻게 계산하는지 수식으로 정확히 알아본다. 추정식은 \(y_{it} = X_{it}\beta + u_{it}\)이며, \(X_{it}\)의 처음 원소는 상수항인 1이다. 즉, 절편이다. 추정식의 양 변에 각 \(i\)별로 \(t\)에 걸친 평균(average)를 취하면 \(\bar{y}_i = \bar{X}_i\beta + \bar{u}_i\)가 된다. 부록 D.2의 수학적 공식에 따르면 RE 공분산 가정 하에서 GLS는 어떤 실수 \(\theta\)에 대하여 모형을 다음과 같이 편환시킨 후 POLS를 하는 것과 동일하다.
\[\begin{equation} \label{eq-ch2-8} \tag{2.8} y_{it} - \theta\bar{y}_i = (X_{it}-\theta\bar{X}_i)\beta + (u_{it}-\theta\bar{u}_i) \end{equation}\]종속변수의 개별 관측치에서 개체별 종속변수의 평균에 어떠한 실수값을 곱한 값을 제해준 것이 설명변수의 개별 관측치에서 마찬가지로 어떠한 실수값을 곱한 설명변수들의 개체별 평균에 오차항에서 개체별 평균 오차항을 빼어준 것과 같다는 것이 된다. 이때, \(\theta\)는 변환된 오차항, \(u_{it}=\theta\bar{u}_i\)가 \(\ref{eq-ch2-7}\)의 RE 공분산 가정 하에서 등분산적이고 시계열 상관이 없도록 하는 값으로 선택된다. 자세한 유도 과정과 증명은 한치록 (2021, 46–48)에서 자세히 설명하고 있다. 결론적으로 \(u_{it}\)를 관측할 수만 있으면 나머지 두 분산—집단내 변동과 집단간 변동을 추정할 수 있는데, 문제는 \(u_{it}\)가 관측되지 않기 때문에 잔차를 이용하고, 어떤 잔차를 이용하느냐에 따라 다양한 추정방법이 가능하다는 것이다.
집단내 회귀로부터 \(\sigma^2_\varepsilon\) 추정량을 구하고, 집단간 회귀로부터 \(\bar{u}_i\) 분산 \((\sigma^2_\mu + \frac{1}{T}\sigma^2_\varepsilon)\)의 추정량을 구한 후 이를 결합하여 \(\sigma^2_\mu\)을 추정한다 (Swamy and Arora 1972).
Note
예제 2.5 인구구조와 총저축율(RE 회귀)
예제 2.2의 모형과 데이터에 대하여 RE 회귀를 해 보자. \(\hat{\theta}\)의 값도 리포트해보도록 하자.
wdi5bal <- pick("http://econ.korea.ac.kr/~chirokhan/panelbook/data/wdi5bal.dta")
model_random2 <- plm::plm(sav ~ age0_19 + age20_29 + age65over + lifeexp +
as.factor(year),
data = wdi5bal, model = "random",
index = c("id", "year"))
summary(model_random2)Oneway (individual) effect Random Effect Model
(Swamy-Arora's transformation)
Call:
plm::plm(formula = sav ~ age0_19 + age20_29 + age65over + lifeexp +
as.factor(year), data = wdi5bal, model = "random", index = c("id",
"year"))
Balanced Panel: n = 96, T = 6, N = 576
Effects:
var std.dev share
idiosyncratic 29.574 5.438 0.411
individual 42.361 6.509 0.589
theta: 0.6772
Residuals:
Min. 1st Qu. Median 3rd Qu. Max.
-20.8482 -2.9237 0.0772 2.8783 28.2744
Coefficients:
Estimate Std. Error z-value Pr(>|z|)
(Intercept) 6.888907 9.329987 0.7384 0.46029
age0_19 -0.291279 0.107012 -2.7219 0.00649 **
age20_29 -0.348563 0.197211 -1.7675 0.07715 .
age65over -1.183850 0.253840 -4.6638 3.105e-06 ***
lifeexp 0.553639 0.077884 7.1085 1.173e-12 ***
as.factor(year)1990 0.280314 0.800939 0.3500 0.72635
as.factor(year)1995 -0.240316 0.819404 -0.2933 0.76931
as.factor(year)2000 -1.291651 0.845039 -1.5285 0.12639
as.factor(year)2005 -0.671415 0.885659 -0.7581 0.44839
as.factor(year)2010 -2.656247 0.940299 -2.8249 0.00473 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Total Sum of Squares: 20014
Residual Sum of Squares: 17116
R-Squared: 0.1448
Adj. R-Squared: 0.1312
Chisq: 95.8317 on 9 DF, p-value: < 2.22e-16model_random2 |> screenreg(digits = 4, include.ci = FALSE, single.row = TRUE,
include.rsquared = TRUE, include.adjrs = TRUE)
==========================================
Model 1
------------------------------------------
(Intercept) 6.8889 (9.3300)
age0_19 -0.2913 (0.1070) **
age20_29 -0.3486 (0.1972)
age65over -1.1838 (0.2538) ***
lifeexp 0.5536 (0.0779) ***
as.factor(year)1990 0.2803 (0.8009)
as.factor(year)1995 -0.2403 (0.8194)
as.factor(year)2000 -1.2917 (0.8450)
as.factor(year)2005 -0.6714 (0.8857)
as.factor(year)2010 -2.6562 (0.9403) **
------------------------------------------
s_idios 5.4382
s_id 6.5085
R^2 0.1448
Adj. R^2 0.1312
Num. obs. 576
==========================================
*** p < 0.001; ** p < 0.01; * p < 0.05STATA와 달리 theta 옵션을 주지 않아도 R에서 summary()는 \(\hat{\theta}\) 값을 표시한다. 관련된 해석은 한치록 (2021, 50)을 살펴보면 된다. POLS로 추정한 결과와 크게 다르지 않다.
RE 공분산 가정이 맞으면 이 RE 추정량은 BLUE와 동일한 대표본 특성을 갖는다. 엄밀하게 말하면 RE 추정 결과는 정확히 BLUE인 것은 아니다. BLUE는 \(\sigma^2_\mu\)과 \(\sigma^2_\varepsilon\)을 알 때 구할 수 있다. 이러한 미세한 차이점을 제외하면 RE 회귀로부터의 추정량은 RE 공분산 가정 \(\ref{eq-ch2-7}\) 하에서 BLUE라고 대충 표현할 수 있고, RE 가정이 정말로 맞으면 변환된 오차항에 이분산이나 자기상관이 거의 없으므로 통상적인 방식으로 구한 표준오차들은 잘 작동한다.
하지만 RE 공분산 가정 \(\ref{eq-ch2-7}\)은 상당히 강한 가정이다. 특히 시간에 따라 변하는 \(\varepsilon_{it}\)가 시간에 걸쳐 비상관이라는 가정은 성립하지 않기 쉽다. RE 공분산 가정 \(\ref{eq-ch2-7}\)가 위배되는 경우, 변형된 오차항 \(u_{it}-\theta\bar{u}_i\)는 이분산이나 시계열 상관을 가질 수 있다. 그러므로 RE 공분산 가정 \(\ref{eq-ch2-7}\)이 옳지 않으면 통상적인 표준오차는 잘못되며, 올바른 추론을 위해서는 RE 회귀와 클러스터 표준오차를 결합하여 사용할 수 있다(♖).
이 클러스터 분산 추정량이 잘 작동하기 위해서는 앞에서와 마찬가지로 \(n\)이 커야 한다(대략 \(n \geq 50\)). \(n\)이 작은 상황이 아니라면 가급적 클러스터 표준오차를 사용하는 것이 좋다.
Note
예제 2.6 임금방정식의 RE 추정(클러스터 표준오차)
예제 2.4의 RE 회귀에 대하여 클러스터 표준오차를 사용한 통계량들은 다음과 같다. 계수 추정 방법은 예제 2.4와 동일하므로 계수 추정값에는 변함이 없으나 클러스터 표준오차를 구하므로ㅡ 표준오차, \(t\)값, \(p\)값, 신뢰구간은 다를 수 있다.
cluster_random <- coeftest(model_random,
vcovHC(model_random, method = "arellano",
type = "HC1", cluster = "group"))
summary(cluster_random) Estimate Std. Error t value Pr(>|t|)
Min. :-0.41586 Min. :7.697e-05 Min. :-15.529 Min. :0.000e+00
1st Qu.: 0.06266 1st Qu.:8.874e-03 1st Qu.: 6.581 1st Qu.:0.000e+00
Median : 0.16093 Median :1.285e-02 Median : 14.103 Median :0.000e+00
Mean : 0.29170 Mean :2.202e-02 Mean : 10.928 Mean :3.076e-05
3rd Qu.: 0.32278 3rd Qu.:1.759e-02 3rd Qu.: 19.422 3rd Qu.:0.000e+00
Max. : 2.75101 Max. :1.920e-01 Max. : 22.722 Max. :5.537e-04 screenreg(cluster_random,
digits = 4, include.ci = FALSE, single.row = TRUE)
=========================================
Model 1
-----------------------------------------
(Intercept) 2.7510 (0.1920) ***
educ 0.0675 (0.0049) ***
tenure 0.0154 (0.0026) ***
tenure^2 -0.0003 (0.0001) ***
isregul 0.1459 (0.0204) ***
female -0.4159 (0.0268) ***
age05 0.0774 (0.0087) ***
age05^2 -0.0010 (0.0001) ***
as.factor(year)2006 0.0610 (0.0095) ***
as.factor(year)2007 0.1190 (0.0102) ***
as.factor(year)2008 0.1759 (0.0108) ***
as.factor(year)2009 0.1871 (0.0124) ***
as.factor(year)2010 0.2377 (0.0133) ***
as.factor(year)2011 0.2908 (0.0146) ***
as.factor(year)2012 0.3334 (0.0155) ***
as.factor(year)2013 0.3797 (0.0167) ***
as.factor(year)2014 0.3969 (0.0179) ***
as.factor(year)2015 0.4289 (0.0200) ***
=========================================
*** p < 0.001; ** p < 0.01; * p < 0.05이 예제에서 확인할 수 있듯(예제 2.4와 비교할 때), 클러스터 표준오차를 사용하는 경우 표준오차가 증가하는 경향을 보인다.
RE 공분산 가정 \(\ref{eq-ch2-7}\)이 옳으면 RE 회귀가 FGLS이나, 이것이 위배되면 RE ghlrnlsms FGLS가 아니며, RE 추정량보다 더 효율적인 추정량이 존재한다(♖). 한치록 (2021, 52)는 다음과 같이 서술하고 있다.
무엇보다도 RE 회귀만으로도 이미 상당한 효율성에 도달하였다고 보기 때문에, \(\ref{eq-ch2-7}\)의 성립 여부와 무관하게 굳이 더 좋은 추정량을 찾으려고 노력하지 않고 RE 회귀로 만족해도 좋다는 것이 필자의 판단이다. 다만 \(\ref{eq-ch2-7}\)이 성립한다고 확신할 수 없는 경우에는 앞에서 설명한 것처럼 클러스터 표준오차를 사용하는 것이 바람직하다.
Note
연습 2.6. 임의효과 모형에서 \(y_{it} - 0.5\bar{y}_i\)를 \(X_{it} - 0.5\bar{X}_i\)에 대하여 OLS 회귀를 하면 그 추정량은 어떤 성질을 갖는가? 이 추정량을 이용하여 가설검정들을 하려면 어떻게 하여야 하는가?
Ans:
Note
연습 2.7. 불균형패널 데이터가 있다고 하자. 임의효과 모형에서 RE 공분산 가정이 옳고 \(\theta_i = 1 - 1/\sqrt{1+T_i\lambda}\)이라 하자. \(\bar{\theta} = n^{-1}\sum^{n}_{i = 1}\theta_i\)일 때, \(y_{it}-\bar{\theta}\bar{y}_i\)를 \(X_{it}-\bar{\theta}\bar{X}_i\)에 대하여 OLS 회귀를 하면 그 추정량은 어떤 성질을 갖는가? 이 추정량을 이용하여 가설검정들을 하려면 어떻게 하여야 하는가? 이 추정방법과 RE 회귀는 동일한가 서로 다른가?
Ans:
오차항에 동시기 횡단면 상관이 있을 때, 이를 고려하여 효율적으로 추정하는 문제를 생각해 보자. 만약 모형에서 시간별 효과를 충분히 통제하지 않아 \(f_t\)가 오차항에 포함되어 있고 이 \(f_t\)가 설명변수들과 독립이라면, \(f_t\)가 \(t\)에 걸쳐서 IID, \(\mu_i\)가 \(i\)에 걸쳐 IID, \(\varepsilon_{it}\)가 \(i\)와 \(t\)에 걸쳐 IID, 그리고 오차의 모든 구성성분들이 서로간에 독립이라는 가정 하에 \(u_{it}\)는 다음 공분산구조를 갖는다.
\[\begin{equation} \label{eq-ch2-11} \tag{2.11} \mathrm{E}(u_{it}u_{js}) = \begin{cases} \sigma^2_{\mu} + \sigma^2_f + \sigma^2_{\varepsilon}, & i = j, t = s\\ \sigma^2_{\mu}, & i = j, t \neq s\\ \sigma^2_, & i \neq j, t = s\\ 0, & i \neq j, t \neq s. \end{cases} \end{equation}\]만약 \(n\)도 크고 \(T\)도 크면 세 모수들 \(\sigma^2_\mu, \sigma^2_f, \sigma^2_\varepsilon\)을 적절히 추정할 수 있고, 이를 활용하여 FGLS를 할 수도 있다. 이를 앞의 RE 추정량과 구별하여 2원(two-way) 임의효과 회귀라고 한다(2중 클러스터 분산추정이 아님!).
그런데 설명변수가 시간에 따른 추세를 갖는다면, 그 추세가 종속변수 내 추세와 무관할 리 없어 계량경제학에서 2원 임의효과 회귀는 별로 사용되지 않는다고 한다(한치록 2021: 54). 이는 정치학에서도 동일하게 적용되는 문제라고 할 수 있다.
주로 모형에 시간 더미를 포함시켜(시간의 효과를 고정효과로 간주하여) \(f_t\)를 통제한다.
Tip
정리하자면, 설명변수의 강외생성이 충족될 때, RE 공분산 가정이 충족되면 RE 추정량은 FGLS 추정량이고 BLUE에 가까운 성질을 갖는다. RE 공분산 가정이 맞지 않아도, 강외생성이 충족되기만 하면 RE 추정량은 여전히 일관적이며 효율성 면에서도 상당히 좋은 성질을 보이지만, 올바른 검정과 추론을 위해서는 견고한 클러스터 표준오차를 사용해야 한다(한치록 2021: 54-55).
2.5 임의효과 존재 여부의 검정
Breusch and Pagan (1980) 은 라그랑지 승수(Lagrange multiplier, LM) 검정에 대해 임의효과를 갖는 오차성분 모형에서 오차항의 모든 구성부분들이 정규분포를 갖는다는 가정 하에 임의효과의 분산이 0임을 검정하는 LM 통계량을 제시하였다. 이 Breusch-Pagan 검정(BP 검정)은 고유오차 \(\varepsilon_{it}\)가 IID임을 가정하며, 그 영가설은 임의효과(\(\mu_i\))의 분산이 0이라는 것이다.
영가설이 옳다면, 오차 \(u_{it}\)가 \(i\)와 \(t\)에 걸쳐 IID이다.
영가설이 기각된다면, 오차 \(u_{it}\)는 \(\mu_i\)로 인하여 특정한 형태의 시계열 상관을 갖는다.
Note
예제 2.7 임의효과 존재에 관한 BP 검정
testfe.dta 데이터를 이용하여 임의효과 존재 여부에 대한 BP 검증을 해보자. 영가설은 임의효과가 존재하지 않아 \(u_{it}\)에 이분산과 자기상관이 없다는 것이다.
testfe <- pick("http://econ.korea.ac.kr/~chirokhan/panelbook/data/testfe.dta")
testfe_random <- plm::plm(y ~ x1 + x2 + z1,
data = testfe, model = "random",
index = c("id", "year"))
summary(testfe_random)Oneway (individual) effect Random Effect Model
(Swamy-Arora's transformation)
Call:
plm::plm(formula = y ~ x1 + x2 + z1, data = testfe, model = "random",
index = c("id", "year"))
Balanced Panel: n = 100, T = 8, N = 800
Effects:
var std.dev share
idiosyncratic 16.4254 4.0528 0.949
individual 0.8807 0.9385 0.051
theta: 0.1635
Residuals:
Min. 1st Qu. Median 3rd Qu. Max.
-18.532565 -1.697244 0.036542 1.573601 22.012117
Coefficients:
Estimate Std. Error z-value Pr(>|z|)
(Intercept) 0.73862 0.17124 4.3134 1.608e-05 ***
x1 0.90413 0.14637 6.1772 6.526e-10 ***
x2 -0.64329 0.15234 -4.2226 2.414e-05 ***
z1 1.88506 0.22672 8.3146 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Total Sum of Squares: 23011
Residual Sum of Squares: 13051
R-Squared: 0.43283
Adj. R-Squared: 0.43069
Chisq: 607.451 on 3 DF, p-value: < 2.22e-16testfe_random |> screenreg(digits = 4, include.ci = FALSE, single.row = TRUE,
include.rsquared = TRUE, include.adjrs = TRUE)
==================================
Model 1
----------------------------------
(Intercept) 0.7386 (0.1712) ***
x1 0.9041 (0.1464) ***
x2 -0.6433 (0.1523) ***
z1 1.8851 (0.2267) ***
----------------------------------
s_idios 4.0528
s_id 0.9385
R^2 0.4328
Adj. R^2 0.4307
Num. obs. 800
==================================
*** p < 0.001; ** p < 0.01; * p < 0.05plm::plmtest(testfe_random)
Lagrange Multiplier Test - (Honda) for balanced panels
data: y ~ x1 + x2 + z1
normal = 2.4155, p-value = 0.007856
alternative hypothesis: significant effectsSTATA의 xttest0과는 달리 오차성분에 대한 정보를 구체적으로 제시하지는 않는다. 하지만 결과는 같다. 검정 결과에 따르면, \(p\) 값은 매우 작고, 따라서 임의효과(\(\mu_i\))의 분산이 0이라는 영가설은 기각된다(한치록 2021: 57).
BP 검정은 오차항의 구성부분들이 서로 독립적이고 일정한 분산의 정규분포를 갖는다는 전제 하에 시작하며, 이분산이나 시계열상관이 존재하는 경우에 대한 논의가 없다. BP 검정에 대한 자세한 이론적 논의는 한치록 (2021, 58)에서 확인할 수 있다.
Note
한치록 (2021, 58–59)에서 BP 검정 통계량을 수동으로 계산하는 예제가 있으나, 여기에서는 생략한다. BP 검정은 \(\varepsilon_{it}\)가 IID인 상황을 염두에 두고 고안된 것이다. \(u_{it} = \mu_i + \varepsilon_{it}\)이므로 \(u_{it}\)에 자기상관이 있다면 이는 오로지 \(\mu_i\)로 인한 것이다.
반면, 만일 \(\varepsilon_{it}\) 자체에 자기상관이 존재하도록 허용하면, 이 자기상관과 \(\mu_i\)로 인한 자기상관이 구분되지 않을 수 있다. 따라서 \(\varepsilon_{it}\)에 자기상관을 허용하면서 \(\mu_i\)의 존재 여부를 검정하는 것은, \(\varepsilon_{it}\) 내 시계열 상관에 대한 특별한 가정을 도입하지 않는 한 불가능하다.
2.6 최우주추정법
오차항의 분산·공분산에 대한 가정 뿐 아니라 그 분포에 대한 가정도 하게 되면 최우추정법(maximum likelihood estimation, MLE)에 따라 모수들을 추정할 수 있다. 특히 \(\mu_i, \varepsilon_{i1}, \dots, \varepsilon_{iT}\)가 서로 간에 독립이고 \(\mu_i \sim N(0, \sigma^2_\mu),\: \varepsilon_{it}\sim N(0, \sigma^2_\varepsilon)\)이라는 가정 하에서 최우(ML) 추정을 할 수 있다.
library(nlme)
mle_random <- lme(y ~ x1 x2, random = ~1 | id, data = sample)
screenreg(mle_random, digits = 4, single.row = TRUE)
Note
예제 2.9 임금방정식의 최우추정
예제 2.4의 임금방정식을 MLE로 추정해보자. R에서는 nlme 패키지를 이용하여 random = ~1 | pid 옵션을 사용한다.
Ans:
library(nlme)
mle_random <- lme(lwage ~ educ + tenure + I(tenure^2) + isregul + female +
age05 + I(age05^2) + as.factor(year),
random = ~1 | pid,
data = klipsbal)
screenreg(mle_random, digits = 4, single.row = TRUE)
===========================================
Model 1
-------------------------------------------
(Intercept) 2.7410 (0.2057) ***
educ 0.0677 (0.0043) ***
tenure 0.0147 (0.0013) ***
tenure^2 -0.0003 (0.0000) ***
isregul 0.1427 (0.0102) ***
female -0.4173 (0.0256) ***
age05 0.0780 (0.0095) ***
age05^2 -0.0010 (0.0001) ***
as.factor(year)2006 0.0615 (0.0105) ***
as.factor(year)2007 0.1200 (0.0105) ***
as.factor(year)2008 0.1775 (0.0106) ***
as.factor(year)2009 0.1891 (0.0107) ***
as.factor(year)2010 0.2402 (0.0108) ***
as.factor(year)2011 0.2937 (0.0110) ***
as.factor(year)2012 0.3367 (0.0111) ***
as.factor(year)2013 0.3836 (0.0113) ***
as.factor(year)2014 0.4013 (0.0116) ***
as.factor(year)2015 0.4337 (0.0118) ***
-------------------------------------------
AIC 645.1401
BIC 787.6314
Log Likelihood -302.5700
Num. obs. 9196
Num. groups: pid 836
===========================================
*** p < 0.001; ** p < 0.01; * p < 0.05최우추정은 극대화(혹은 극소화) 문제를 수치적으로 푸는 것이므로 연산을 반복하면서 가능도(likelihood)를 최대화하려고 한다. STATA에서는 이러한 반복하는 과정(iteration)이 명시적으로 나타나지만, R에서는 summary() 함수를 이용하면 Linear mixed-effects model fit by REML라고 표시되는 것을 확인할 수 있다. ML 추정 결과와 RE 추정 결과는 상당히 유사하다.
Note
연습 2.9. 예제 2.5의 저축률 데이터와 모형에 대하여 R을 이용하여 MLE 추정을 하라. 계수 추정값들은 RE 추정값과 유사한가? 유사하다면 왜 유사하겠는가? 조금이라도 차이가 있다면 왜 차이가 있겠는지 설명하라.
Ans:
wdi5bal <- pick("http://econ.korea.ac.kr/~chirokhan/panelbook/data/wdi5bal.dta")
mle_random2 <- plm::plm(sav ~ age0_19 + age20_29 + age65over + lifeexp +
as.factor(year),
data = wdi5bal, model = "random",
index = c("id", "year"))
mle_random2 <- lme(sav ~ age0_19 + age20_29 + age65over + lifeexp +
as.factor(year),
random = ~1 | id, data = wdi5bal)
screenreg(list(model_random2, mle_random2), digits = 4, single.row = F)
=================================================
Model 1 Model 2
-------------------------------------------------
(Intercept) 6.8889 5.6002
(9.3300) (9.3408)
age0_19 -0.2913 ** -0.2805 **
(0.1070) (0.1073)
age20_29 -0.3486 -0.3439
(0.1972) (0.1961)
age65over -1.1838 *** -1.1825 ***
(0.2538) (0.2554)
lifeexp 0.5536 *** 0.5662 ***
(0.0779) (0.0786)
as.factor(year)1990 0.2803 0.2792
(0.8009) (0.7941)
as.factor(year)1995 -0.2403 -0.2376
(0.8194) (0.8135)
as.factor(year)2000 -1.2917 -1.2876
(0.8450) (0.8407)
as.factor(year)2005 -0.6714 -0.6688
(0.8857) (0.8840)
as.factor(year)2010 -2.6562 ** -2.6585 **
(0.9403) (0.9420)
-------------------------------------------------
s_idios 5.4382
s_id 6.5085
R^2 0.1448
Adj. R^2 0.1312
Num. obs. 576 576
AIC 3832.2422
BIC 3884.3054
Log Likelihood -1904.1211
Num. groups: id 96
=================================================
*** p < 0.001; ** p < 0.01; * p < 0.05계수값들은 비교적 유사하다. 임의효과 모형이나 MLE 모형이나 모두 동일한 오차 공분산 구조를 상정하기 때문이다. 다만, 조금의 차이는 존재하는데, 그 차이는 각 방식이 \(\sigma^2_\mu/\sigma^2_\varepsilon\)을 구하는 데 차이가 있기 때문이다.
RE와 MLE의 차이는 오직 \(\lambda\), 즉 \(\theta\)의 추정 방식에 있다. 그 결과, 설명변수들의 강외생성이 성립하는 한 RE 가정 \(\ref{eq-ch2-7}\)이 성립하지 않아도 RE 추정량이 일관적인 것처럼, MLE에 사용되는 RE 과정과 정규분포 가정이 성립하지 않더라도 \(\hat{\lambda}\)이 무언가로 수렵하는 한 정규분포 가정에 입각한 MLE는 여전히 일관적이다. 일관성의 측면에서 이 MLE는 오차 분포의 비정규성(non-normality)이나 이분산, 자기상관 등에 견고하다(한치록 2021: 63).
2.7 선형 PA 모형의 GEE 추정
2.2절의 POLS는 모집단 평균 모형(Population-Averaged model, PA 모형)의 GEE(Generalized Estimating Equations) 추정과 관련되어 있다. PA 모형이란 각 \(t\)에서 모집단의 평균적인 횡단면 관계(population average)를 나타내는 모형이다. 각 \(t\)의 종속변수가 \(\mathrm{E}(y_{it}|X_{it}) = \alpha + X_{it}\beta + \delta_t\)의 함수관계를 갖는다는 모형을 세워보자. 이 모형은 \(t\)기에 존재하는 모집단 내 개체들 간의 함수관계를 표현하는 PA 모형으로, 동일 개체 내의 변화가 아니라 개체 간 비교에 집중한다.
PA 모형의 추정을 위해 가장 많이 사용되는 방법은 LIANG and ZEGER (1986) 가 제안한 GEE 추정법이다. 이 방법은 \(y_{it}\)의 평균들에 관한 PA 모형에 대하여, \(y_{it}\)의 개체 내 시점 간 상관에 관한 주어진 가정 하에서 계수를 추정한다. 이 개체 내 상관에 대한 가정으로는 ‘독립’, ‘교환가능’, ‘자기회귀’ 등을 포함한 여러 가지 중 하나를 사용할 수 있다.
- 이때 중요한 것은 각 시점에서 \(y_{it}\)의 평균에 관한 모형 \(\mathrm{E}(y_{it}|X_{it}) = \alpha + X_{it}\beta + \delta_t\)만 맞으면 나머지 가정이 틀렸어도 \(n\rightarrow \infty\)일 때, GEE 추정량은 여전히 일관적이라는 것이다. 개체 내 상관에 관한 가정이 틀렸으면 클러스터 표준오차를 사용하여 분산추정량을 보정한다.
이 PA 모형에 대해 오차항 \(u_{it}\)가 \(t\)에 걸쳐 독립이라는 가정 하에서 구한 GEE 추정량은 바로 POLS 추정량이다. 이 추정량을 LIANG and ZEGER (1986) 는 “Independence Estimating Equations” 추정량이라고 한다. R에서 y를 x에 대하여 POLS하려면 다음 명령어 중 하나를 사용하면 된다.
위의 명령들은 확률변수들이 \(t\) 간에 서로 독립적이라는 가정을 한 상태에서 GEE로 추정한 것이다. 하지만 확률변수들이 \(t\) 간에 서로 독립적이지 않더라도 \(\mathrm{E}(y_{it}|X_{it}) = \alpha + X_{it}\beta + \delta_t\)가 성립하기만 하면 이 GEE 추정량은 일관성을 갖는다.
Note
연습 2.10.의 데이터와 회귀 모형에 대하여 xtgee 명령어를 사용한 추정 결과들이 reg를 사용한 POLS 겨로가와도 동일한지 확인하라.
Ans:
re_cluster <- lm_robust(lwage ~ educ + tenure + I(tenure^2) + isregul +
female + age05 + I(age05^2) + as.factor(year),
clusters = pid,
data = klipsbal)
library(geepack)
xtgee_ind <- geeglm(lwage ~ educ + tenure + I(tenure^2) + isregul +
female + age05 + I(age05^2) + as.factor(year),
id = pid, family=gaussian, corstr="ind",
data = klipsbal)
modelsummary::modelsummary(list(re_cluster, xtgee_ind),
fmt = 4, "html")| Model 1 | Model 2 | |
|---|---|---|
| (Intercept) | 2.9839 | 2.9839 |
| (0.1963) | (0.1911) | |
| educ | 0.0562 | 0.0562 |
| (0.0047) | (0.0046) | |
| tenure | 0.0332 | 0.0332 |
| (0.0041) | (0.0039) | |
| I(tenure^2) | −0.0004 | −0.0004 |
| (0.0002) | (0.0001) | |
| isregul | 0.2717 | 0.2717 |
| (0.0275) | (0.0273) | |
| female | −0.3892 | −0.3892 |
| (0.0247) | (0.0246) | |
| age05 | 0.0651 | 0.0651 |
| (0.0088) | (0.0086) | |
| I(age05^2) | −0.0009 | −0.0009 |
| (0.0001) | (0.0001) | |
| as.factor(year)2006 | 0.0525 | 0.0525 |
| (0.0097) | (0.0097) | |
| as.factor(year)2007 | 0.0973 | 0.0973 |
| (0.0106) | (0.0105) | |
| as.factor(year)2008 | 0.1421 | 0.1421 |
| (0.0109) | (0.0109) | |
| as.factor(year)2009 | 0.1450 | 0.1450 |
| (0.0121) | (0.0121) | |
| as.factor(year)2010 | 0.1891 | 0.1891 |
| (0.0131) | (0.0131) | |
| as.factor(year)2011 | 0.2323 | 0.2323 |
| (0.0140) | (0.0140) | |
| as.factor(year)2012 | 0.2695 | 0.2695 |
| (0.0149) | (0.0148) | |
| as.factor(year)2013 | 0.3050 | 0.3050 |
| (0.0153) | (0.0152) | |
| as.factor(year)2014 | 0.3131 | 0.3131 |
| (0.0164) | (0.0163) | |
| as.factor(year)2015 | 0.3398 | 0.3398 |
| (0.0180) | (0.0180) | |
| Num.Obs. | 9196 | 9196 |
| R2 | 0.597 | 0.597 |
| AIC | 7745.4 | 7745.4 |
| BIC | 7880.8 | 7880.8 |
| Log.Lik. | −3853.702 | |
| F | 167.945 | |
| RMSE | 0.37 | 0.37 |
| Std.Errors | by: pid |
거의 결과가 유사하지만 표준오차의 추정에서 약간의 차이가 존재하는 것을 확인할 수 있다.
2.4절의 RE 회귀는 \(y_{it} = X_{it}\beta+u_{it}\)에서 \(u_{it}\)의 분산이 동일하고(등분산) 상이한 시점 간 공분산이 시점을 막론하고 모두 동일하다(교환가능)는 가정 하에서 2단계(two-step)로 FGLS를 하는 것이다. 이와 유사한 방법으로, \(u_{it}\)의 \(t\)간 상관관계가 교환가능하다는 가정을 똑같이 하면서 GEE 추정을 할 수도 있다.
xtgee_ex <- geeglm(y ~ x1 + x2,
id = id, family = gaussian, corstr = "ex",
data = sample)이 PA 추정의 결과는 RE 회귀의 결과와 정확히 같지는 않지만 상당히 유사하다.
Note
연습 2.11. 예제 2.6의 데이터와 회귀 모형에 대하여 오차항(\(u_{it}\))의 공분산이 교환가능(exchangeable)하다는 가정 하에서 PA 모형의 GEE 추정을 하라. 이때, 견고한 클러스터 표준오차를 사용하라. 이 결과와 예제 2.6의 결과가 유사한지 확인하라.
Ans:
library(geepack)
xtgee_ex <- geeglm(lwage ~ educ + tenure + I(tenure^2) + isregul + female +
age05 + I(age05^2) + as.factor(year),
id = pid, family=gaussian, corstr="ex",
data = klipsbal)
xtgee_ex_cl <- coeftest(xtgee_ex,
vcovHC(xtgee_ex, method="arellano",
type="HC1", cluster="group"))
screenreg(list(xtgee_ex_cl, cluster_random),
digits = 4, single.row = F,
custom.model.names = c("PA GEE Robust Cluster SE", "RE Cluster SE"))
============================================================
PA GEE Robust Cluster SE RE Cluster SE
------------------------------------------------------------
(Intercept) 2.7413 *** 2.7510 ***
(0.0778) (0.1920)
educ 0.0677 *** 0.0675 ***
(0.0023) (0.0049)
tenure 0.0148 *** 0.0154 ***
(0.0008) (0.0026)
tenure^2 -0.0003 *** -0.0003 ***
(0.0000) (0.0001)
isregul 0.1428 *** 0.1459 ***
(0.0063) (0.0204)
female -0.4173 *** -0.4159 ***
(0.0119) (0.0268)
age05 0.0780 *** 0.0774 ***
(0.0033) (0.0087)
age05^2 -0.0010 *** -0.0010 ***
(0.0000) (0.0001)
as.factor(year)2006 0.0614 *** 0.0610 ***
(0.0010) (0.0095)
as.factor(year)2007 0.1200 *** 0.1190 ***
(0.0016) (0.0102)
as.factor(year)2008 0.1775 *** 0.1759 ***
(0.0022) (0.0108)
as.factor(year)2009 0.1891 *** 0.1871 ***
(0.0032) (0.0124)
as.factor(year)2010 0.2401 *** 0.2377 ***
(0.0039) (0.0133)
as.factor(year)2011 0.2937 *** 0.2908 ***
(0.0046) (0.0146)
as.factor(year)2012 0.3366 *** 0.3334 ***
(0.0053) (0.0155)
as.factor(year)2013 0.3835 *** 0.3797 ***
(0.0063) (0.0167)
as.factor(year)2014 0.4012 *** 0.3969 ***
(0.0069) (0.0179)
as.factor(year)2015 0.4336 *** 0.4289 ***
(0.0080) (0.0200)
============================================================
*** p < 0.001; ** p < 0.01; * p < 0.05거의 결과가 유사하지만 표준오차의 추정에서 약간의 차이가 존재하는 것을 확인할 수 있다.
Breusch, T. S., and A. R. Pagan. 1980. “The Lagrange Multiplier Test and Its Applications to Model Specification in Econometrics.” The Review of Economic Studies 47 (1): 239–53. https://doi.org/10.2307/2297111.
Cameron, A. Colin, and Douglas L. Miller. 2015. “A Practitioner’s Guide to Cluster-Robust Inference.” Journal of Human Resources 50 (2): 317–72. https://doi.org/10.3368/jhr.50.2.317.
LIANG, KUNG-YEE, and SCOTT L. ZEGER. 1986. “Longitudinal Data Analysis Using Generalized Linear Models.” Biometrika 73 (1): 13–22. https://doi.org/10.1093/biomet/73.1.13.
Swamy, P. A. V. B., and S. S. Arora. 1972. “The Exact Finite Sample Properties of the Estimators of Coefficients in the Error Components Regression Models.” Econometrica 40 (2): 261–75. https://doi.org/10.2307/1909405.
Thompson, Samuel B. 2011. “Simple Formulas for Standard Errors That Cluster by Both Firm and Time.” Journal of Financial Economics 99 (1): 1–10. https://doi.org/10.1016/j.jfineco.2010.08.016.
Zellner, Arnold. 1962. “An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias.” Journal of the American Statistical Association 57 (298): 348–68. https://doi.org/10.1080/01621459.1962.10480664.
한치록. 2021. 패널데이터강의. Third. 박영사.
더미변수의 경우, 기준이 되는 준거집단을 제외한 나머지 집단에 대한 값들을 모델에 투입한다. 예를 들어, 어떠한 종속변수에 대한 봄, 여름, 가을, 겨울의 관계를 더미변수로 살펴본다고 하자. 이때, 더미변수는 사계절 중 하나를 제외한 여름, 가을, 겨울만 모델에 투입한다. 그리고 그 결과로 얻어지는 세 개의 계수값은 “봄에 비해 여름은 평균적으로 ~”와 같이 해석된다. 또한 더미변수의 계수값은 절편의 차이라고 볼 수 있다. 즉, 봄이었을 때의 평균적인 절편값에 비하여 여름의 평균적 절편값의 차이가 여름의 계수값이다.↩︎
이때, \(\mathbb{X}\)는 모든 \(i\)와 \(t\)에 걸쳐 모은 것이다.↩︎
\(s = 1, 2, \dots, T\).↩︎